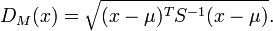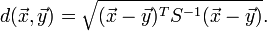Mahalanobis Distance(马氏距离)
(from:http://en.wikipedia.org/wiki/Mahalanobis_distance)
Mahalanobis distance
In statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936.It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs fromEuclidean distance in that it takes into account the correlations of the data set and is scale-invariant. In other words, it is a multivariateeffect size.
Definition
Formally, the Mahalanobis distance of a multivariate vector 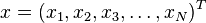 from a group of values with mean
from a group of values with mean 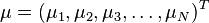 and covariance matrix
and covariance matrix 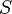 is defined as:
is defined as:
(注:1.这个是X和总体均值的马氏距离。2.这里的S是可逆的,那么协方差矩阵不可逆的话怎么办?)
Mahalanobis distance (or "generalized squared interpoint distance" for its squared value) can also be defined as a dissimilarity measure between two random vectors  and
and  of the same distribution with the covariance matrix
of the same distribution with the covariance matrix 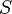 :
:
If the covariance matrix is the identity matrix, the Mahalanobis distance reduces to the Euclidean distance. If the covariance matrix is diagonal, then the resulting distance measure is called the normalized Euclidean distance:
where 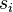 is the standard deviation of the
is the standard deviation of the 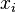 (
(  ) over the sample set.
) over the sample set.
(源自:百度百科)
马氏优缺点:
Mahalanobis Distance(马氏距离)的更多相关文章
- paper 114:Mahalanobis Distance(马氏距离)
(from:http://en.wikipedia.org/wiki/Mahalanobis_distance) Mahalanobis distance In statistics, Mahalan ...
- Mahalanobia Distance(马氏距离)的解释
马氏距离有多重定义: 1)可以表示 某一个样本与DataSet的距离. 2)可以表示两个DataSet之间的距离. 1) The Mahalanobis distance of an observat ...
- 马氏距离(Mahalanobis distance)
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离.它是一种有效的计算两个未知样本集的相似度的方法.与欧 ...
- MATLAB求马氏距离(Mahalanobis distance)
MATLAB求马氏距离(Mahalanobis distance) 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 1.马氏距离计算公式 d2(xi, ...
- Mahalanobis距离(马氏距离)的“哲学”解释
讲解教授:赵辉 (FROM : UESTC) 课程:<模式识别> 整理:PO主 基础知识: 假设空间中两点x,y,定义: 欧几里得距离, Mahalanobis距离, 不难发现,如果去掉马 ...
- 有关马氏距离和hinge loss的学习记录
关于度量学习,之前没有看太多相关的文献.不过南京的周老师的一篇NIPS,确实把这个问题剖析得比较清楚. Mahalanobis距离一般表示为d=(x-y)TM(x-y),其中x和y是空间中两个样本点, ...
- 基于欧氏距离和马氏距离的异常点检测—matlab实现
前几天接的一个小项目,基于欧氏距离和马氏距离的异常点检测,已经交接完毕,现在把代码公开. 基于欧式距离的: load data1.txt %导入数据,行为样本,列为特征 X=data1; %赋值给X ...
- Python实现的计算马氏距离算法示例
Python实现的计算马氏距离算法示例 本文实例讲述了Python实现的计算马氏距离算法.分享给大家供大家参考,具体如下: 我给写成函数调用了 python实现马氏距离源代码: # encod ...
- Levenshtein Distance莱文斯坦距离算法来计算字符串的相似度
Levenshtein Distance莱文斯坦距离定义: 数学上,两个字符串a.b之间的莱文斯坦距离表示为levab(|a|, |b|). levab(i, j) = max(i, j) 如果mi ...
随机推荐
- 【英语】Bingo口语笔记(28) - 表示“秘密”
- 动态加载 移除js file
动态加载.移除.替换js/css文件 stylesheetjavascriptcssfunctionnull <script language="javascript"> ...
- 基于HTTP 协议认证介绍与实现
导言 一直对http 的头认证有兴趣,就是路由器的那种弹出对话框输入账号密码怎么实现一直不明白,最近,翻了一下http 协议,发现这是一个RFC 2617的实现,所以写篇文章介绍一下吧. Http基本 ...
- uploadify scriptData参数无法传参的问题
最近需要使用到uploadify,需要向后台传递参数,使用script最多只能够传递一个参数,当然也可以通过合并参数然后再在服务器段拆分参数的方法来传递多个参数,而uploadify插件提供的scri ...
- Android adb shell命令大全
1. 显示系统中全部Android平台: android list targets 2. 显示系统中全部AVD(模拟器): android list avd 3. 创建AVD(模拟器): androi ...
- AJAX overrideMimeType作用
我们经常在AJAX代码中发现如下代码: if (http_request.overrideMimeType) { http_request.overrideMimeType("te ...
- visual asssit 过期提示
把目录下的VA_X.dll文件复制到上面所说的文件夹下覆盖源文件即可 对于vs2010的朋友需要额外注意,使用2010的朋友,是需要覆盖到Visual Studio 2010的Visual Assis ...
- web开发利器 fiddler
http://mccxj.github.io/blog/20130531_introduce-to-fiddler.html
- T-SQL:SQL Server-数据开发(经典)
ylbtech-SQL Server-Doc-Help:SQL Server-数据开发(经典) SQL Server 数据开发(经典). 1,数据开发(经典) 返回顶部 1.按姓氏笔画排序: Sele ...
- UIImageView 点击放大缩小
static CGRect oldframe; -(void)showImage:(UIImageView *)avatarImageView{ UIImage *image=avatarImageV ...