2016-2017 ACM-ICPC, NEERC, Southern Subregional Contest (Online Mirror, ACM-ICPC Rules, Teams Preferred) 几道简单题的题解

A. Toda 2

题意：给你n个人，每个人的分数是a[i]，每次可以从两个人到五个人的使得分数减一，使得最终的分数相等；

思路:假设答案为m；每个人的分数与答案m的差值为d[i]，sum为d[i]的总和，max为d[i]的最大值；仅当sum-max>=max的时候才满足；

　　 满足之后，总和为奇数，先取三个，再取两个（都是最大与次大值）；偶数每次取两个即可；

B. Minimum and Maximum

题意：人机交互题；给你一个数组 ，找出其中的最小值与最大值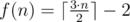，需要在询问f(n)的次数内得到最大值与最小值；

　　　每次询问，？ i  j表示i和j的下标，告诉你哪个大，相等或者小，得到答案；

思路：类似与归并排序的思想，每次取两个，得到最大最小值；

G. Car Repair Shop

题意：给你n个区间，起点和长度；当当前区间与前面的区间有交集的时候，找到另外一个相同长度的区间放进去；

思路：模拟，先有一个大区间，每次插入一个区间，把这个区间修改成空白点的，把那个大区间拆成两个小区间，如果原来的区间内有空白，从1开始查找是否有长度

　　　大于当前长度的区间，放入；

　　　set模拟；

H. Delete Them

队友写的；

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double Pi = acos(-1.0);
const int N = 1e3+, M = 2e5+, mod = 1e9+, inf = 2e9;

int a[N],n,m,pos[N],H[N];
char s[N][N];
set<int > S;
int main() {
       scanf("%d%d",&n,&m);
       for(int i = ; i <= n; ++i) scanf("%s",s[i]);

       for(int i = ; i <= m; ++i) scanf("%d",&pos[i]),H[pos[i]]=;
       sort(pos+,pos+m+);
       for(int i = ; i <= m; ++i)  S.insert(strlen(s[pos[i]]));

       if(S.size() > ) {
        puts("No");
        return ;
       }

       for(int i = ; i <= m; ++i) {
        for(int j=;j<strlen(s[pos[i]]); ++j) {
            if(s[pos[]][j]!=s[pos[i]][j])  {
                s[pos[]][j] = '?';
            }
        }
       }
       for(int i = ;i<=n; ++i) if(!H[i]) {
        int len = strlen(s[i]);
        int sum = ;
        if(len!=strlen(s[pos[]])) continue;
        for(int j = ; j < len; ++j) {
            if(s[pos[]][j] == '?') sum++;
            else if(s[pos[]][j] == s[i][j]) sum++;
        }
        if(sum == len) {
            puts("No");
            return ;
        }

       }
       puts("Yes");
       printf("%s\n",s[pos[]]);
}

J. Bottles

题意：给你n个瓶子，第一行a[i]表示第i个瓶子的剩余水的容量，第二行b[i]表示第i个瓶子的体积；

　　　你需要使用最少的瓶子数量，装完剩下全部的水，每次改变n单位的水的花费n；　

思路：k很好求，贪心求法，开始以为n就100，写个暴搜+剪枝，TLE TEST 42；

　　　后面发现就一个背包，只是这个背包需要求的是恰好装满这个背包大小的最大价值；

　　　剩余水的质量为sum1，瓶子的体积和sum2；你需要找到sum1-sum2之间的最大值；

　　　dp[k][sum1]-dp[k][sum2];

　　　复杂度（k*sum2*n）；

　　　优化下可以（k*sum1*n）；

J. Bottles

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Nick has n bottles of soda left after his birthday. Each bottle is described by two values: remaining amount of soda ai and bottle volumebi (ai ≤ bi).

Nick has decided to pour all remaining soda into minimal number of bottles, moreover he has to do it as soon as possible. Nick spends xseconds to pour x units of soda from one bottle to another.

Nick asks you to help him to determine k — the minimal number of bottles to store all remaining soda and t — the minimal time to pour soda into k bottles. A bottle can't store more soda than its volume. All remaining soda should be saved.

Input

The first line contains positive integer n (1 ≤ n ≤ 100) — the number of bottles.

The second line contains n positive integers a1, a2, ..., an (1 ≤ ai ≤ 100), where ai is the amount of soda remaining in the i-th bottle.

The third line contains n positive integers b1, b2, ..., bn (1 ≤ bi ≤ 100), where bi is the volume of the i-th bottle.

It is guaranteed that ai ≤ bi for any i.

Output

The only line should contain two integers k and t, where k is the minimal number of bottles that can store all the soda and t is the minimal time to pour the soda into k bottles.

Examples

input

4
3 3 4 3
4 7 6 5

output

2 6

input

2
1 1
100 100

output

1 1

input

5
10 30 5 6 24
10 41 7 8 24

output

3 11

Note

In the first example Nick can pour soda from the first bottle to the second bottle. It will take 3 seconds. After it the second bottle will contain 3 + 3 = 6 units of soda. Then he can pour soda from the fourth bottle to the second bottle and to the third bottle: one unit to the second and two units to the third. It will take 1 + 2 = 3 seconds. So, all the soda will be in two bottles and he will spend 3 + 3 = 6seconds to do it.