滑动窗口（poj，线段树维护区间最值）

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

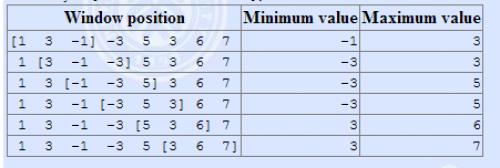
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

思路：

一般人切这道题都用的st表或者是单调队列

我手残打了个线段树（其实是因为我太菜了不会上面两个）

我线段树维护两个值，一个是区间最大值，一个是区间最小值

每次修改，在修改完叶子结点（单点插入，我当做修改处理）后，我向上pushup更新区间最值

每个节点表示的是他所负责的线段的区间最值

查询常规查询即可

代码：

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define rii register int i
#define rij register int j
#define rs 1048576
#define inf 1<<30
using namespace std;
struct nod{
    long long ma,mi;
}x[];
int n,k;
void add(long long wz,long long l,long long r,long long val,long long bh)
{
    if(l==r&&l==wz)
    {
        x[bh].mi=val;
        x[bh].ma=val;
        return;
    }
    long long ltt=(l+r)/;
    if(wz>ltt)
    {
        add(wz,ltt+,r,val,bh*+);
    }
    else
    {
        add(wz,l,ltt,val,bh*);
    }
    x[bh].mi=min(x[bh*].mi,x[bh*+].mi);
    x[bh].ma=max(x[bh*].ma,x[bh*+].ma);
}
struct cs{
    int maxn,minx;
}ans;
cs query(long long l,long long r,long long nl,long long nr,long long bh)
{
    if(l<nl)
    {
        l=nl;
    }
    if(r>nr)
    {
        r=nr;
    }
    cs an,bn;
    an.maxn=-inf;
    an.minx=inf;
    bn.maxn=-inf;
    bn.minx=inf;
    if(l==nl&&r==nr)
    {
        int ltt=x[bh].ma;
        int kkk=x[bh].mi;
        an.maxn=ltt;
        an.minx=kkk;
        return an;
    }
    int ltt=(nl+nr)/;
    if(l<=ltt)
    {
        an=query(l,r,nl,ltt,bh*);
    }
    if(r>ltt)
    {
        bn=query(l,r,ltt+,nr,bh*+);
    }
    an.maxn=max(an.maxn,bn.maxn);
    an.minx=min(an.minx,bn.minx);
    return an;
}
long long minn[];
int main()
{
    for(rii=;i<=;i++)
    {
        x[i].ma=-inf;
        x[i].mi=inf;
    }
    scanf("%d%d",&n,&k);
    for(rii=;i<=n;i++)
    {
        long long ltt;
        scanf("%lld",&ltt);
        add(i,,rs,ltt,);
    }
    for(rii=;i<=n-k+;i++)
    {
        ans=query(i,i+k-,,rs,);
        printf("%d ",ans.minx);
        minn[i]=ans.maxn;
    }
    printf("\n");
    for(rii=;i<=n-k+;i++)
    {
        printf("%d ",minn[i]);
    }
}