CF2.C

C. Vladik and fractions

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Vladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction as a sum of three distinct positive fractions in form .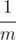

Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that 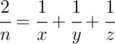. Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 10⁹.

If there is no such answer, print -1.

Input

The single line contains single integer n (1 ≤ n ≤ 10⁴).

Output

If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 10⁹, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.

If there are multiple answers, print any of them.

Examples

Input

3

Output

2 7 42

Input

7

Output

7 8 56

题意：

给出n，问有没有三个数x,y,z,使得1/x+1/y+1/z=2/n;

代码：

 //直接模拟，枚举比2/n小的分数，从1/(n/2+1)开始到2/n-1/(n/2+1)结束，这样依次得到x,y,z，记住分子分母要约分要
 //防止超过1e9，判断x,y,z是否符合条件即可。
 #include<bits\stdc++.h>
 typedef long long ll;
 using namespace std;
 ll gcd(ll x,ll y)
 {
     if(y==) return x;
     return gcd(y,x%y);
 }
 int main()
 {
     int n;
     while(cin>>n)
     {
         if(n==)
         {
             cout<<"-1\n";
             continue;
         }
         ll f1,f2,maxn,minn,f3,f4,x,y,z;
         if(n&)
         {
             f1=;f2=n;
         }
         else
         {
             f1=;f2=n/;
         }
         minn=(f2+)/f1;
         maxn=f2*minn;
         int flag=;
         for(ll i=minn;i<=maxn;i++)
         {
             x=i;
             f4=i*f2;
             f3=f1*i-f2;
             ll cnt=gcd(f4,f3);
             f4/=cnt;f3/=cnt;
             y=(f4+)/f3;
             z=y*f4;
             ll tem=f3*y-f4;
             cnt=gcd(z,tem);
             z/=cnt;tem/=cnt;
             if(x==y||x==z||z==y||tem!=||x<=||y<=||z<=||z>1e9||y>1e9||z>1e9)
                 continue;
             flag=;
             break;
         }
         if(flag) cout<<x<<" "<<y<<" "<<z<<endl;
         else cout<<"-1\n";
     }
     return ;
 }
 //本题这样做就麻烦了，其实只有n=1时不能拆成三个分数相加，其余的数都可以拆成1/n,1/(n+1),1/n*(n+1);
 #include<bits\stdc++.h>
 using namespace std;
 int main()
 {
     int n;
     cin>>n;
     if(n==) cout<<"-1\n";
     else
         cout<<n<<" "<<n+<<" "<<n*(n+)<<endl;
     return ;
 }