《C程序设计II》简易计算器，杨辉，数字杯子图形

《C程序设计II》简易计算器，杨辉，数字杯子图形。《C程序设计II》简易计算器，杨辉，数字杯子图形。《C程序设计II》简易计算器，杨辉，数字杯子图形。

《C程序设计II》简易计算器，杨辉，数字杯子图形。《C程序设计II》简易计算器，杨辉，数字杯子图形。《C程序设计II》简易计算器，杨辉，数字杯子图形。《C程序设计II》简易计算器，杨辉，数字杯子图形。

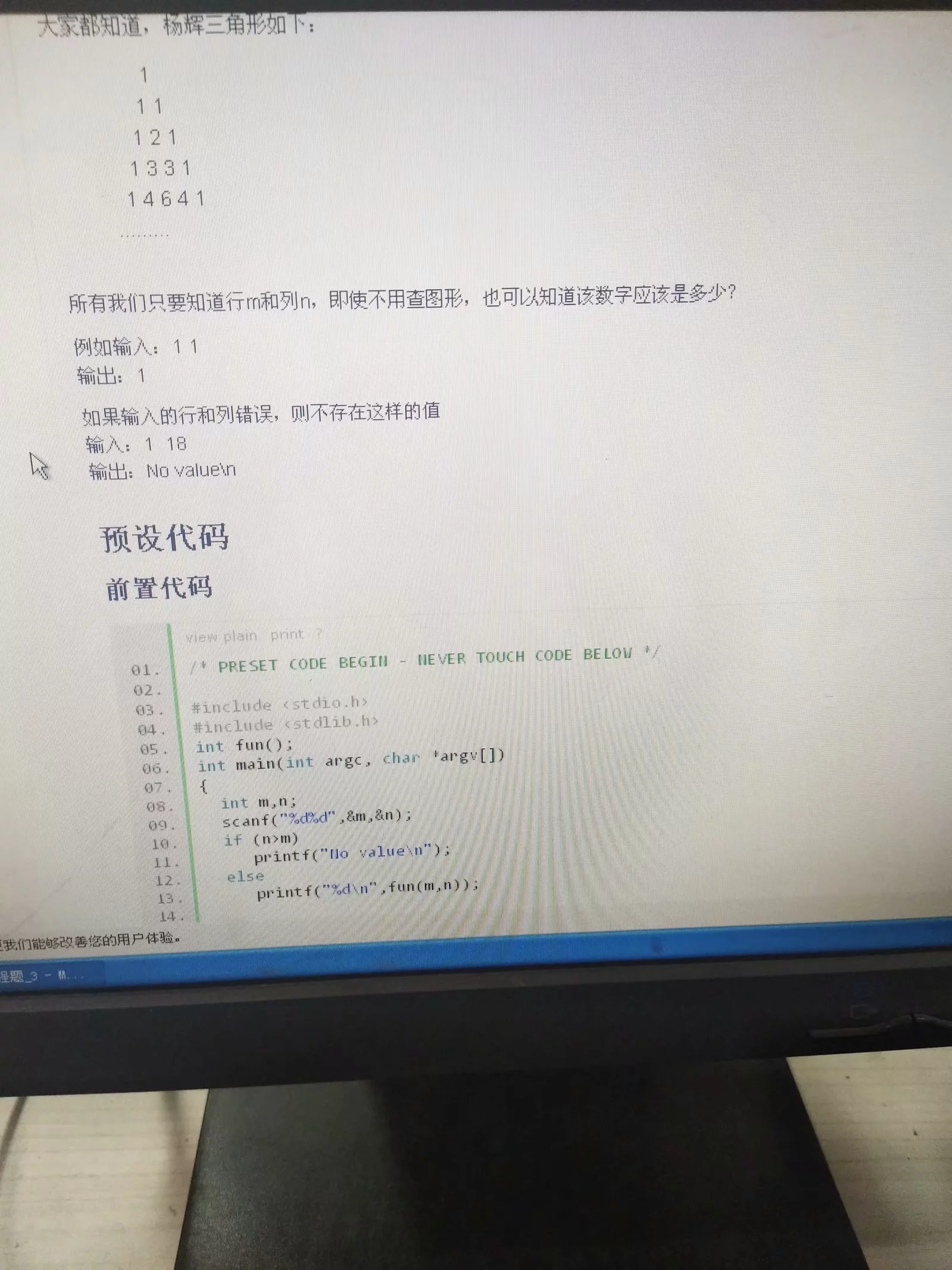
#include<stdio.h>
#include<stdlib.h>
int fun(int m,int n){
    int a[][],i,j,num;
    for(i=;i<;i++)
    {
        for(j=;j<;j++)
            a[i][j]=;
    }
    for(i=;i<;i++)
        a[i][]=;
    for(i=;i<;i++)
        for(j=;j<=i;j++)
            a[i][j]=a[i-][j]+a[i-][j-];
    return a[m][n];
}
int main(){
    int m,n;
    scanf("%d%d",&m,&n);
    if(n>m){
        printf("NO Value!");
    }else{
        printf("%d\n",fun(m,n));
    }
    return ;
}

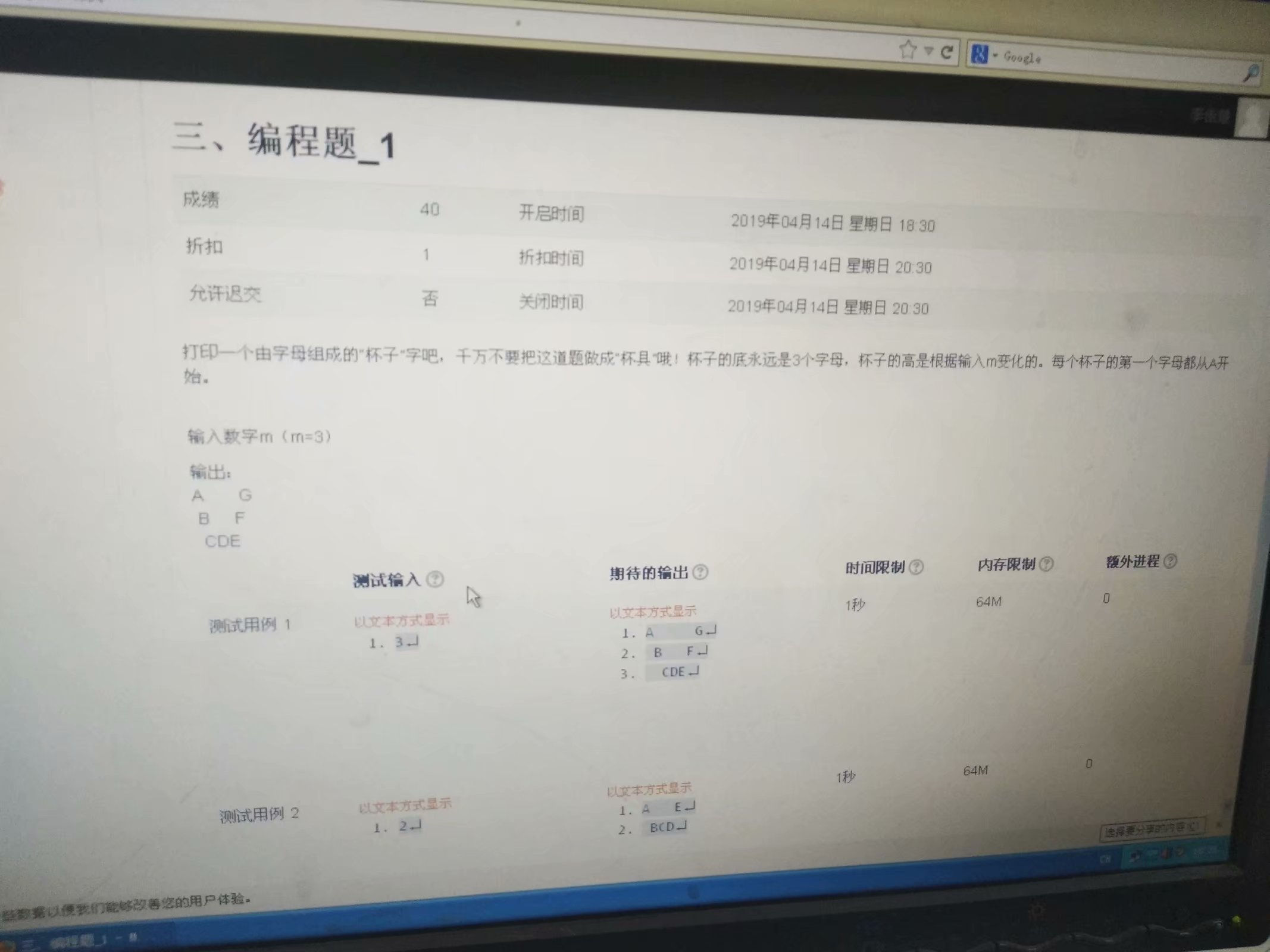
#include<stdio.h>
#include<stdlib.h>
int main(){
    int m,i,j,p;
    char t='A',x;
    scanf("%d",&m);
    char f='A'+(m*);
    p=m+;
    for(i=;i<m;i++){
        for(j=;j<i;j++){
            printf("*");
        }
        printf("%c",t);
        if(i==m-){
            x=t;
                printf("%c",++x);
                p--;
        }
        for(j=(p-=);j>;j--){
            printf(" ");
        }
        printf("%c",f);
        printf("\n");
        t++;
        f--;
    }
    return ;
}

实现一个建议计算器：

输入

3

1，2，3

+,*

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
char a1[]={};
int a[]={};
int main(){
    int i=,t,sum=,flag=,p;
    char op[]={'\0'};
    scanf("%d",&t);
    getchar();
    gets(a1);
    gets(op);
    p=;
    for(i=;i<strlen(a1);i++){
        if(a1[i]>=''&&a1[i]<=''){
            a[p++]=a1[i]-'';
        }
    }
    for(i=;i<strlen(op);i++){
        if(op[i]==',') continue;
        if(op[i]=='+'){
          if(flag){
              sum=a[i]+a[i+];
              flag=;
          }else{
              sum+=a[i];
          }
        }else if(op[i]=='-'){
            if(flag){
              sum=a[i]-a[i+];
              flag=;
          }else{
              sum-=a[i];
          }
        }else if(op[i]=='*'){
            if(flag){
              sum=a[i]*a[i+];
              flag=;
          }else{
              sum*=a[i];
          }
        }else if(op[i]=='/'){
            if(flag){
              sum=a[i]/a[i+];
              flag=;
          }else{
              sum/=a[i];
          }
        }
    }
    printf("%d",sum);
    return ;
}