快速莫比乌斯变换（FMT）

快速莫比乌斯变换（FMT）

原文出处：虞大的博客。此仅作蒟蒻本人复习用~

给定两个长度为n的序列 \(a_0, a_1, \cdots, a_{n-1}\)和\(b_0, b_1, \cdots, b_{n-1}\)，你需要求出一个序列\(c_0, c_1, \cdots, c_{n-1}\)，其中\(c_k\)满足：\(c_k = \sum\limits_{i \mid j = k} a_i b_j\)。其中|表示按位或。\(n \leq 10^6\)表示序列长度。

显然发现\(i∣j=k\)这个条件不怎么好处理，如果我们作一个集合的 "前缀和" ，即令\(P_i = \sum\limits_{j \subseteq i} p_j\)（\(i\&j=j\)），那么有：\(C_k = \sum_{k_0 \subseteq k} c_i = \sum_{k_0 \subseteq k} \sum_{i \cup j = k_0} a_i b_j = \sum_{i \cup j \subseteq k} a_i b_j = \left( \sum_{i \subseteq k} a_i \right) \left( \sum_{j \subseteq k} b_j \right) = A_k \cdot B_k\)

所以说我们就把集合并卷积转化成了两个“前缀和”集合的\(O(n)\)运算，和FFT差不多。现在的问题就是怎么快速算出这些“前缀和”集合。

我们可以画一张图，图中每一行代表一个\(P_i\)。这一行有哪些格子涂蓝，就代表它是哪些\(p_i\)的和：

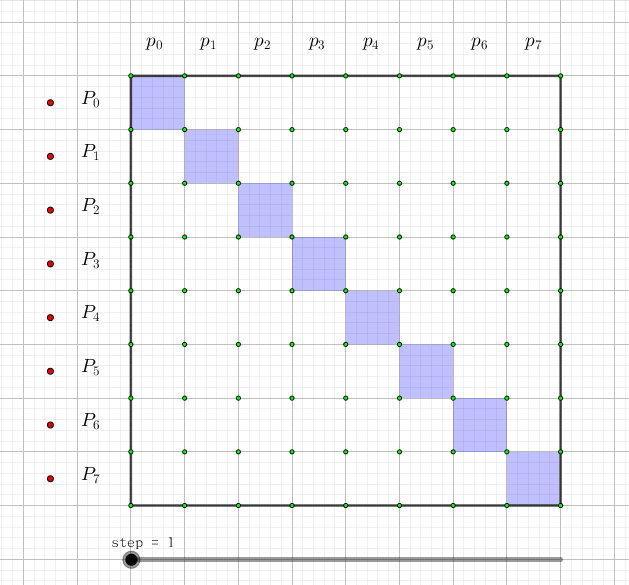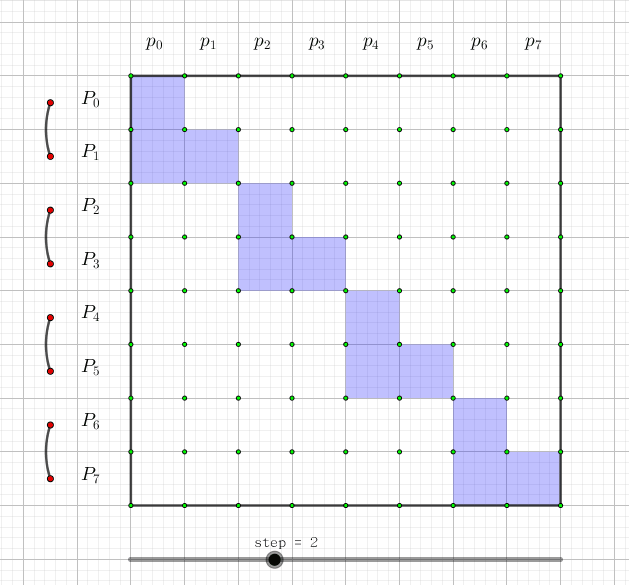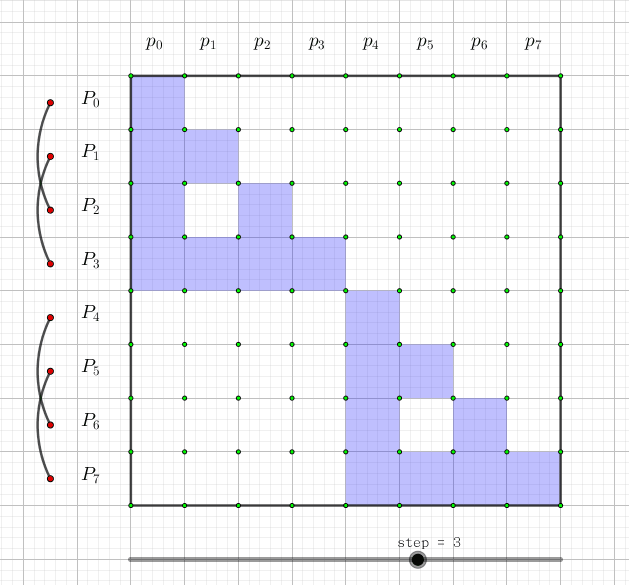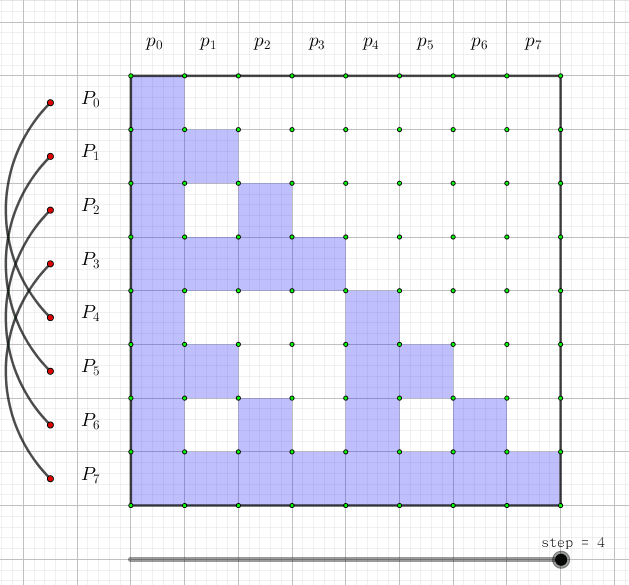
如果用动态规划来理解的话，令\(f[i][j]\)表示j的开头\(2^i\)个数中为权值为1的数的和， 那么转移显然就是\(f[i+1][j+2^i]+=f[i][j]\)(j的\(2^i\)位是0)。其中j这一维是可以压掉的。

如果改变一下你脑海中的求和顺序，那么循环内的一次加法，就相当于一个集合的前面2^i个元素的值被加上了。

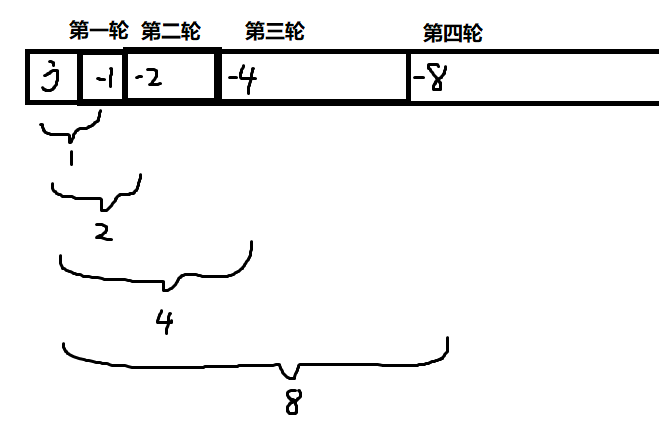
如果要把\(f\)还原该怎么办呢？只要把+=改成-=就行了~（不会证，但是真的很好记）

#include <cctype>
#include <cstdio>
using namespace std;

typedef long long LL;
const LL maxn=2e6+5;
LL n, l, bits, a[maxn], b[maxn], c[maxn];

void FMT(LL *f, LL flag){
	for (LL i=0; i<bits; ++i)
		for (LL j=0; j<l; ++j)
			if ((j>>i&1)==0) f[j|1<<i]+=(~flag?f[j]:-f[j]);
}

inline void getint(LL &x){
	char ch; x=0;
	for (; ch=getchar(), !isdigit(ch););
	for (x=ch-48; ch=getchar(), isdigit(ch);)
		x=(x<<3)+(x<<1)+ch-48;
}

int main(){
	getint(n); l=1;
	while (l<n) l<<=1, ++bits;
	for (LL i=0; i<n; ++i) getint(a[i]); FMT(a, 1);
	for (LL i=0; i<n; ++i) getint(b[i]); FMT(b, 1);
	for (LL i=0; i<l; ++i) c[i]=a[i]*b[i]; FMT(c, -1);
	//坑点1：乘法可能爆LL 坑点二：i要到l
	for (LL i=0; i<n; ++i) printf("%lld ", c[i]);
	return 0;
}