显著水平|区间估计|假设检验|显著性|第一类错误|Ⅱ类错误|β错误|t检验|连续性矫正|二项分布的假设检验|样本百分率|
第三章 假设检验
区间估计与假设检验的基本区别?
上一章中讨论了置信区间的估计方法。它是利用样本数据,以抽样总体的分布为理论基础,用一定的概率保证来计算出原总体中未知参数的区间范围。特别值得注意的是:在作区间估计之前,我们对所要估计的参数是一无所知的。
§ 而在这一章中,我们所要做的工作是,先对要研究的参数作一个假设,然后去检验这个假设是否正确。因此假设检验对于所研究的参数总是先有一个假设的值。
§ 这也是这两种方法最基本的区别。
显著水平(significance level)或概率水平(probability level)是什么?
置信度
如何解释“显著性”?
具有显著性:假设值与真实值之间有随机误差,也有真实误差。
不具有显著性:假设值与真实值之间只有随机误差,没有真实误差。
第一类错误是何含义?
理解一:真实情况是表面误差是随机误差的概率至少是(1-α)。真实情况是表面误差是真实误差和随机误差的概率不会超过α。真实情况是表面误差是真实误差和随机误差,而估计情况是表面误差是随机误差,所以估计错误,所以事件“真实情况是表面误差是真实误差和随机误差,而估计情况是表面误差是随机误差,所以估计错误”的概率不会超过α。即第一类错误。
理解二:假设检验已结束,其结果(显著或者不显著)可能出错的概率不会超过是α,不会出错的概率至少是(1-α)。
理解三:假阴性,原来是真的,却被判定是假的。
Ⅱ类错误、β错误是何含义?
理解一:以为估计出来的分布与原分布是一个分布,实际上是另一个分布的概率。
理解二:假阳性,原来是假的,却被认为是真的。
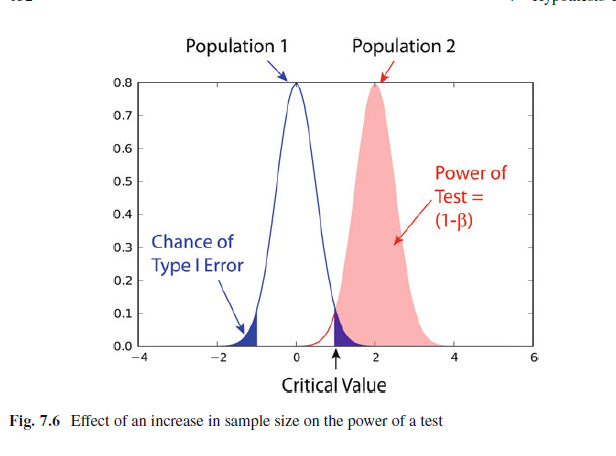
即如上图,你以为应该支持H1,即原分布是population1,但是其实真实情况是population2。因为population1中的点造成了这个错误,所以概率是population1中有population2的点。
单边假设检验的假设有何特点?
H0:相等
H1:小于|大于,不是小于或大于,是只有小于,或者只有大于

在样本平均数与总体平均数差异显著性检验中,实际过程中如何获知总体平均数?
已知的总体平均数μ一般为一些公认的理论数值、经验数值或期望数值。
什么是t检验法?
t 检验法,就是在显著性检验时利用 t分布进行概率计算的检验方法。
百分率数服从二项分布,在单值与总体检验的过程中需要注意有,在大样本上有连续性矫正的情况
当满足n足够大,p不过小,np>5或者nq<30的条件时,可近似地采用u检验法,就是有连续性矫正,即正态近似法来进行显著性检验;
若np和nq均大于30,不必对u进行连续性矫正。
这里的p、q是H0假设中的值
二项分布的假设检验的特殊之处在哪里?
二项分布是单因素p,所以只用假设p相同。
什么时候进行连续性矫正?
当满足n足够大,p不过小,np>5或者nq<30的条件时,可近似地采用u检验法,就是有连续性矫正,即正态近似法来进行显著性检验;
样本百分率与总体百分率差异显著性检验的连续性矫正是什么?

样本百分率与总体百分率差异显著性检验的连续性矫正是什么?
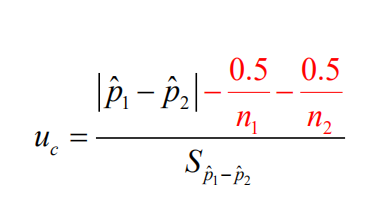
显著水平|区间估计|假设检验|显著性|第一类错误|Ⅱ类错误|β错误|t检验|连续性矫正|二项分布的假设检验|样本百分率|的更多相关文章
- Tomcat启动报错org.springframework.web.context.ContextLoaderListener类配置错误——SHH框架
SHH框架工程,Tomcat启动报错org.springframework.web.context.ContextLoaderListener类配置错误 1.查看配置文件web.xml中是否配置.or ...
- log4j中Logger.getLogger()加载一个类提示错误
转载自:https://blog.csdn.net/q3229270/article/details/77986687 ----------------------------- 错误提示如下:The ...
- 解决Android studio生成H文件时报找不到类文件错误
今天整理思路时觉得在native直接调用java的方法显示这个办法挺不错 于是就用到了生成H文件 可能我的编译环境和他们的不一样 网上的教程如下 javah -d ../jni com.jm.prom ...
- 导入Maven项目后,Eclipse提示“Missing artifact ”类的错误
导入Maven项目后,Eclipse提示“Missing artifact ”类的错误 标签: Maven Missing art 2016-08-15 16:05 679人阅读 评论(0) 收藏 举 ...
- 网易云课堂_C++程序设计入门(下)_第9单元:白公曾咏牡丹芳,一种鲜妍独“异常”_第9单元 - 作业5:OJ编程 - 使用异常进行图形类的错误处理
第9单元 - 作业5:OJ编程 - 使用异常进行图形类的错误处理 查看帮助 返回 温馨提示: 1.本次作业属于Online Judge题目,提交后由系统即时判分. 2.学生可以在作业截止时间之前 ...
- UnsupportedClassVersionError : 不支持的类版本错误
UnsupportedClassVersionError : 不支持的类版本错误 listenerStart配置类的应用程序侦听器时出错 listenerStart Error configuring ...
- 2×c列联表|多组比例简式|卡方检验|χ2检验与连续型资料假设检验
第四章 χ2检验 χ2检验与连续型资料假设检验的区别? 卡方检验的假设检验是什么? 理论值等于实际值 何条件下卡方检验的需要矫正?如何矫正? 卡方检验的自由度如何计算? Df=k-1而不是n-1 卡方 ...
- 转载: Javah生成JNI头文件出现找不到类的错误
错误: 找不到 'com.chnic.jni.SayHellotoCPP' 的类文件. 上图可以看到错误和解决办法. 不要忘记那个点 javah -classpath . -jni com.chnic ...
- 实体类注解错误:Could not determine type for: java.util.List
今天配置实体类注解时,出现以下错误: Caused by: org.hibernate.MappingException: Could not determine type for: java.uti ...
随机推荐
- hdu 1277 全文检索 (字典树应用)
全文检索 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submis ...
- HDU 5477: A Sweet Journey
A Sweet Journey Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) ...
- c++ opencv显示对话框
IplImage *pl = cvLoadImage("e:\\3.bmp", 1); cvNamedWindow("123", 1); cvShowImage ...
- 微服务中一个项目install打包总是失败
在微服务的一个项目中install打包时总是报错如下: [INFO] Scanning for projects... [INFO] [INFO] -------------------------- ...
- Python开源库的bug
scipy 在misc的pilutil.py中def fromimage(im, flatten=0)函数中, # workaround for crash in PIL, see #1613.im. ...
- COGS 1489玩纸牌
%%%http://blog.csdn.net/clover_hxy/article/details/53171234 #include<bits/stdc++.h> #define LL ...
- Unity 可重复随机数
出处 https://blogs.unity3d.com/cn/2015/01/07/a-primer-on-repeatable-random-numbers/ (英文原版) http://ww ...
- c++的符号表的肤浅认识
符号表是编译期产生的一个hash列表,随着可执行文件在一起 示例程序 int a = 10; int b; void foo(){ static int c=100; } int main(){ in ...
- python单链表的基本操作思路
单链表: 1.定义链表 class ListNode: # 定义节点 def __init__(self, x): self.val = x # 节点当前值 self.next = None # 指向 ...
- Linux|Zookeeper--CentOS7开机启动Zookeeper
参考 https://www.cnblogs.com/zhangmingcheng/p/7455278.html 在 /etc/rc.d/init.d 下创建zookeeper脚本 #!/bin/ba ...
