洛谷 P3811 【模板】乘法逆元（欧拉定理&&线性求逆元）

题目传送门

逆元定义

逆元和我们平时所说的倒数是有一定的区别的，我们平时所说的倒数是指：a*(1/a) = 1，那么逆元和倒数之间的区别就是：假设x是a的逆元，那么 a * x = 1(mod p)，也就是只多了一个取余的操作，这个取余的操作，就会保证a的逆元不一定只是a的倒数。那么我们的逆元有什么作用呢？

并且取余还不满足下面式子：( a/b )%p = (a%p  /  b%p)  %  p ,那么我们如果遇到b过大必须在中间过程进行取余的操作，那么我们会发现在乘法中满足：(a*b) % p = (a%p  *  b%p) %p,那么我们只要将上面式子转换为下面乘法的式子就可以了

我们用inv(b)来表示b的逆元，那么他一定满足：b*inv(b) = 1(mod p)    ==>  b = 1/inv(b) ，那么我们代入上面的除法的式子：(a/b)%p =     (a * inv(b)) %p = (a%p  *  inv(b)%p) % p

这样我们就可以根据逆元来将除法取余的式子转换为乘法取余的式子
原文：https://blog.csdn.net/li1615882553/article/details/80001473

一：欧拉定理求逆元

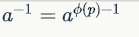
 #include<iostream>
 #include<cstdio>

 using namespace std;

 long long m,k,n,sum,s;

 inline long long phi(long long x) {
     long long res = x,a = x;
     for(int i = ;i * i <= a; i++)
         if(a % i == ) {
             res = res / i * (i - );
             while(a % i == )
                 a = a / i;
         }
     if(a > )
         res = res / a * (a - );
     return res;
 }

 inline void _out(long long pp,long long v) {
     sum = ;
     while(pp > ) {
         if(pp %  != )
             sum = (sum * v) % m;
         pp = pp / ;
         v = (v * v) % m;
     }
     printf("%d\n",sum);
 }

 int main() {
     scanf("%d%d",&n,&m);
     k = phi(m);
     s = k - ;
     for(int i = ;i <= n; i++)
         _out(s,i);
     return ;
 }

欧拉定理

但因为欧拉定理求逆元时间复杂度为O(nlongn)，所以本题会被卡两个点。

二：线性求逆元

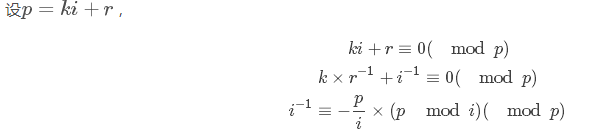
 #include<iostream>
 #include<cstdio>

 using namespace std;

 int n,inv[];
 long long p;

 int main() {
     inv[] = ;
     scanf("%d%lld",&n,&p);
     for(int i = ;i <= n; i++)
         inv[i] = (p - p / i) * inv[p % i] % p;
     for(int i = ;i <= n; i++)
         printf("%d\n",inv[i]);
     return ;
 }

线性

因为是线性，O(n)足够优秀，所以轻松过掉本题