E - Rebuild UVALive - 7187 (二次函数极值问题)

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5531

Problem Description

Archaeologists find ruins of Ancient ACM Civilization, and they want to rebuild it.

The ruins form a closed path on an x-y plane, which has n endpoints. The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively. Endpoint i and endpoint i−1 are adjacent for 1<i≤n, also endpoint 1 and endpoint n are adjacent. Distances between any two adjacent endpoints are positive integers.

To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri. All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.

Note that ri must not be less than 0 since we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.

You are given the coordinates of n endpoints. Your task is to find r1,r2,…,rn which makes sum of base area of all pillars as minimum as possible.

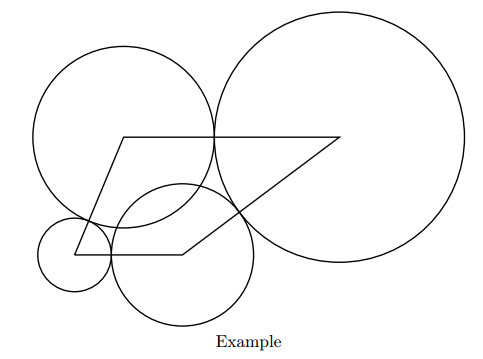
For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12), we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25). The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816…. Note that we count the area of the overlapping parts multiple times.

If there are several possible to produce the minimum sum of base area, you may output any of them.

 

Input

The first line contains an integer t indicating the total number of test cases. The following lines describe a test case.

The first line of each case contains one positive integer n, the size of the closed path. Next n lines, each line consists of two integers (xi,yi) indicate the coordinate of the i-th endpoint.

1≤t≤100
3≤n≤104
|xi|,|yi|≤104
Distances between any two adjacent endpoints are positive integers.

 

Output

If such answer doesn't exist, then print on a single line "IMPOSSIBLE" (without the quotes). Otherwise, in the first line print the minimum sum of base area, and then print n lines, the i-th of them should contain a number ri, rounded to 2 digits after the decimal point.

If there are several possible ways to produce the minimum sum of base area, you may output any of them.

 

Sample Input

3
4
0 0
11 0
27 12
5 12
5
0 0
7 0
7 3
3 6
0 6
5
0 0
1 0
6 12
3 16
0 12

 

Sample Output

988.82
3.75
7.25
12.75
9.25
157.08
6.00
1.00
2.00
3.00
0.00
IMPOSSIBLE

 

Source

2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）

 

Recommend

hujie

题解:对于题目分析可得一些性质:

1:一个圆的半径确定,其他的圆的半径也随之确定.

2:对于n,分奇偶讨论,奇数情况下化简可得:若有解必有唯一解,否则无解.偶数情况下构造二次函数有一变元,从而转换为二次函数的极值问题.

3:限制:半径必须都>=0

#include <bits/stdc++.h>
#define met(a, b) memset(a, b, sizeof(a))
#define ll long long
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
typedef pair<int,int>P;
const int maxn=;
const double eps=1e-;
const double pi=acos(-);
P p[maxn];
double d[maxn],f[maxn];
double dist(P a,P b)
{
  return sqrt((a.first-b.first)*(a.first-b.first)+(a.second-b.second)*(a.second-b.second));
}
int main()
{
  int T;
  cin>>T;
  while(T--){
    int n;
    cin>>n;
    for(int i=;i<=n;i++)cin>>p[i].first>>p[i].second;
    for(int i=;i<=n;i++){
      if(i==n)d[i]=dist(p[i],p[]);
      else d[i]=dist(p[i],p[i+]);
    }
    double maxx=0x3f3f3f3f,minn=;//极值上下限
    f[]=;
    for(int i = ; i <=n ; i++)
    {
      f[i] = d[i-] - f[i-];
      if(i%== && f[i] < maxx)//若为偶数点,则该圆的半径只能减小这么多(即第一个圆的半径只能增大这么多),更新最大值下限
      {
        maxx = f[i];
      }
      if(i%== && (-f[i]) > minn)//若为奇数点,且此时f[i]小与0,则必须第一个圆的半径更新为该值,更新最小值上限
      {
        minn = -f[i];
      }
    }
    if(minn >= maxx + eps )//无解
    {
      printf("IMPOSSIBLE\n");
      continue;
    }
    if(n%==){//奇数个点,有解则必有唯一解,否则无解
      double x=;//第一个圆的半径x=(d1-d2+d3-d4...)/2,唯一解.
      for(int i=;i<=n;i++){
        if(i%==)x+=d[i];
        else x-=d[i];
      }
      x/=;
      if(x<=minn-eps||x>=maxx+eps){
        cout<<"IMPOSSIBLE"<<endl;
        continue;
      }
      double area=;
      for(int i=;i<=n;i++){
        if(i%==)area+=(f[i]+x)*(f[i]+x);
        else area+=(f[i]-x)*(f[i]-x);
      }
      area*=pi;
      printf("%.2f\n",area);
      for(int i=;i<=n;i++){
        if(i%==)printf("%.2f\n",f[i]+x);
        else printf("%.2f\n",f[i]-x);
      }
    }
    else{//偶数情况构造二次函数,y=a*x*x+b*x+c
      double now=;
      for(int i=;i<=n;i++){
        if(i%==)now+=d[i];
        else now-=d[i];
      }
      if(fabs(now)>eps||minn-maxx>eps){
        cout<<"IMPOSSIBLE"<<endl;
        continue;
      }
      double a=n;
      double b=,c=;
      for(int i=;i<=n;i++){
        if(i%==){
          b+=*f[i];
        }
        else{
          b-=*f[i];
        }
        c+=f[i]*f[i];
      }
      double x=-b/(*a);
      if(x<minn+eps)x=minn;
      if(x>maxx-eps)x=maxx;
      double area=a*x*x+b*x+c;
      area*=pi;
      printf("%.2f\n",area);
      for(int i=;i<=n;i++){
        if(i%==)printf("%.2f\n",f[i]+x);
        else printf("%.2f\n",f[i]-x);
      }
    }
  }
  return ;
}