K：剑指offer-56 题解 谁说数字电路的知识不能用到算法中？从次数统计到数字电路公式推导，一文包你全懂

前言：

本题解整理了一位大佬在leetcode中的代码的方法，该博文致力于让所有人都能够能够看懂该方法。为此，本题解将从统计数字出现次数的解题方式开始讲起，再推导出逐位统计的解题方式，期望以循序渐进的方式得出最终代码的思想。

相关知识关键字：

二进制、位运算、真值表、逻辑表达式、状态机

题目：

剑指offer 56 II. 数组中数字出现的次数 II

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

示例 1：

输入：nums = [3,4,3,3]

输出：4

示例 2：

输入：nums = [9,1,7,9,7,9,7]

输出：1

题解：

对于数组nums，其只有一个数字出现了一次，其余数字均出现了三次，一种直观的想法是直接采用一个map统计各个字符出现的次数，最后再遍历map中的各个键值对，直到找到只出现了一次的数字。其代码如下

    public int singleNumber(int[] nums) {
        //统计各个数字出现的次数，键为数字，值为出现的次数
        Map<Integer,Integer> map =new HashMap<Integer,Integer>();
        for(int i:nums){
            if(!map.containsKey(i)){
                map.put(i,1);
                continue;
            }
            map.put(i,map.get(i)+1);
        }
        //遍历map中的键值对，查看值出现次数为1的键，即为答案
        int result = 0;
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){
            if(entry.getValue()==1){
                result = entry.getKey();
                break;
            }
        }
        return result;
    }

对于该解题方法，其空间复杂度为O（n），时间复杂度为O（n），这显然不会是该题的最优解。

在得出逐位运算的解题方式之前，我们需要研究下该数组中的数字用二进制的方式进行表示的特点。

以题干给出的示例1为例，nums=[3,4,3,3]，将数组中各个数字采用二进制的方式写出，

3 = （0011）2

4 = （0100）2

3 = （0011）2

3 = （0011）2

通过对数组中各个数的二进制表示形式逐位进行观察，我们可以发现，当数组中只出现一次的那个数字(用k表示)在二进制的对应位为0时，该对应位为1在数组各个数字中出现的总次数应当为3^n ，当k的对应位为1时，该对应位为1在数组各个数字中出现的总次数应当为 3^n + 1，为此，我们可以统计数字中的各个位中1出现的次数，当为3^n 次时，只出现一次的数字的对应位应当为0，当为3^n + 1次时，只出现一次的数字的对应位应当为1。由此，我们可以得到如下代码：

    public int singleNumber(int[] nums) {
        if(nums==null||nums.length==0) return 0;
        int result = 0;
        for(int i = 0;i<32;i++){
            //统计该位1的出现次数情况
            int count = 0;
            int index = 1<<i;
            for(int j:nums){
                //该位与操作后的结果不为0，则表示该位为1的情况出现了
                if((index&j)!=0){
                    count++;
                }
            }
            //该位上出现1的次数mod3后为1，表示出现一次的数字该位为1
            if(count%3==1){
                result|=index;
            }
        }
        return result;
    }

对于该解题方法，其时间复杂度为O（n），空间复杂度为O（1）。在某种程度上，这是最优解了。但是，该题解仍有改进的空间（其时间复杂度的常系数为32）。

有了对数组中数字的各二进制位进行逐一统计分析出现次数的相关基础后，我们便可以推导出那个击败100%的答案的解法了。回顾上面的解题方法的分析部分，其需要我们对数字的二进制位逐位进行统计，对于int数据类型，我们需要遍历32次数组（int占4字节），以便统计出各个二进制位出现的次数。那我们有没有办法只遍历一次数组便得出答案呢？当然有，我们可以一次分析32bit的int的各个位在数组的各个数字中出现的次数。在分析上面的代码我们可以发现，实际上，我们只需要记录对应位出现的次数为0、1、2次的情况，当对应位出现次数为3的时候，我们便可以将该位出现的次数置为0,重新开始进行计数。由于int型中的各个二进制位出现的次数为3进制的，为此我们需要两个位来记录各个位出现的次数，由此我们需要引入两个变量a，b来统计对应位出现的次数。由ab两个变量组合起来来记录各个二进制位出现为1的情况。变量a表示高位的情况，变量b表示低位的情况，而在遍历数组运算完成之后，遍历b的值便是答案。

变量ab组合的各个二进制位组合的形式有如下三种，考虑进新引入的变量c的各二进制位的情况，我们可以得到如下真值表：

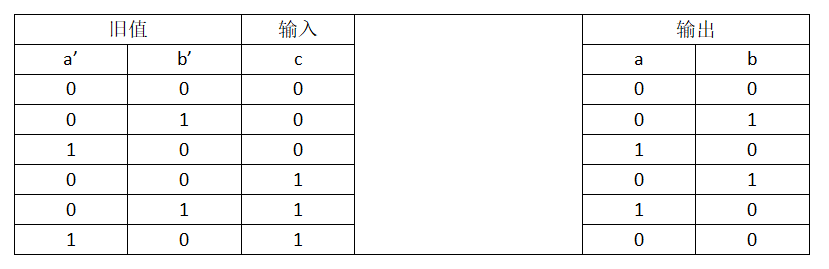
由以上真值表，我们便可得出变量a，b的逻辑表达式，其表示如下

a = a’(!b’)(!c)+(!a’)b’c

b = (!a’)b’(!c)+(!a’)(!b’)c = (!a’)[b’(!c)+(!b’)c] = (!a’)[b’^c]

由此，我们可以得到如下代码

    public int singleNumber(int[] nums) {
        //a对应位为1表示出现2次的记录，b对应位表示出现1次或0次的记录，ab共同组成该位出现的次数
        int a = 0,b =0;
        for(int i:nums){
            int temp = a;
            a = (~a&b&i)|(a&~b&~i);
            b = ~temp&(b^i);
        }
        return b;
    }

实际上，我们还能对a的逻辑表达式进行简化，先得到b的逻辑表达式，之后用b代替b’作为输入，由此可以简化a为

a = (!a’)(!b)c+a’(!b)(!c) = (!b)[(!a’)c+a’(!c)] = (!b)[a’^c]

由此，我们可以得到如下代码

    public int singleNumber(int[] nums) {
        //a为对应位的1出现2次的记录，b为对应位出现1次的记录，ab共同组成该位出现的次数
        int a = 0,b =0;
        for(int i:nums){
            b = ~a&(b^i);
            a = ~b&(a^i);
        }
        return b;
    }

至此，我们得到了最终的代码。

---

这个是本人的公众号，致力于写出绝大部分人都能读懂的技术文章。欢迎相互交流，我们博采众长，共同进步。