吴裕雄--天生自然 R语言开发学习：主成分分析和因子分析（续一）

#--------------------------------------------#
# R in Action (2nd ed): Chapter 14           #
# Principal components and factor analysis   #
# requires package psych                     #
# install.packages("psych")                  #
#--------------------------------------------#
 
par(ask=TRUE)
set.seed(1234) # make results reproducible
 
# Listing 14.1 - Principal components analysis of US Judge Ratings
library(psych)
pc <- principal(USJudgeRatings[,-1], nfactors=1)
pc
 
# Principal components analysis Harman23.cor data
library(psych)
fa.parallel(Harman23.cor$cov, n.obs=302, fa="pc", n.iter=100,
            show.legend=FALSE, main="Scree plot with parallel analysis")
 
# Listing 14.2 - Principal components analysis of body measurements
library(psych)
PC <- principal(Harman23.cor$cov, nfactors=2, rotate="none")
PC
 
# Listing 14.3 - Principal components analysis with varimax rotation
rc <- principal(Harman23.cor$cov, nfactors=2, rotate="varimax")
rc
 
# Listing 14.4 - Obtaining componenet scores from raw data
library(psych)
pc <- principal(USJudgeRatings[,-1], nfactors=1, score=TRUE)
head(pc$scores)
cor(USJudgeRatings$CONT, pc$score)
 
# Listing 14.5 - Obtaining principal component scoring coefficients
library(psych)
rc <- principal(Harman23.cor$cov, nfactors=2, rotate="varimax")
round(unclass(rc$weights), 2)
 
## Exploratory factor analysis of ability.cov data
 
options(digits=2)
library(psych)
covariances <- ability.cov$cov
# convert covariances to correlations
correlations <- cov2cor(covariances)
correlations
 
# determine number of factors to extract
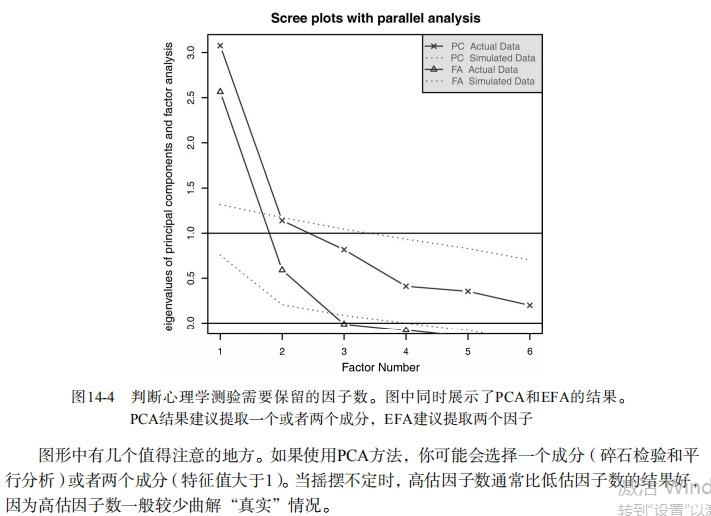
fa.parallel(correlations, n.obs=112, fa="both", n.iter=100,
            main="Scree plots with parallel analysis")
 
# Listing 14.6 - Principal axis factoring without rotation
fa <- fa(correlations, nfactors=2, rotate="none", fm="pa")
fa
 
# Listing 14.7 - Factor extraction with orthogonal rotation
fa.varimax <- fa(correlations, nfactors=2, rotate="varimax", fm="pa")
fa.varimax
 
# Listing 14.8 - Factor extraction with oblique rotation
fa.promax <- fa(correlations, nfactors=2, rotate="promax", fm="pa")
fa.promax
 
# calculate factor loading matrix
fsm <- function(oblique) {
  if (class(oblique)[2]=="fa" & is.null(oblique$Phi)) {
    warning("Object doesn't look like oblique EFA")
  } else {
    P <- unclass(oblique$loading)
    F <- P %*% oblique$Phi
    colnames(F) <- c("PA1", "PA2")
    return(F)
  }
}
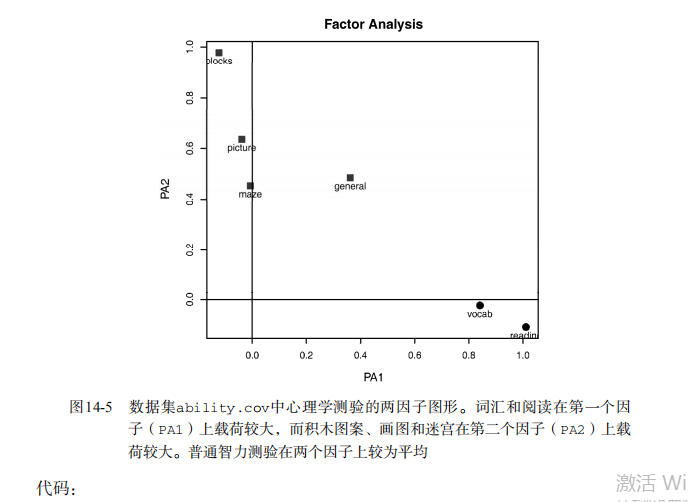
fsm(fa.promax)
 
# plot factor solution
factor.plot(fa.promax, labels=rownames(fa.promax$loadings))
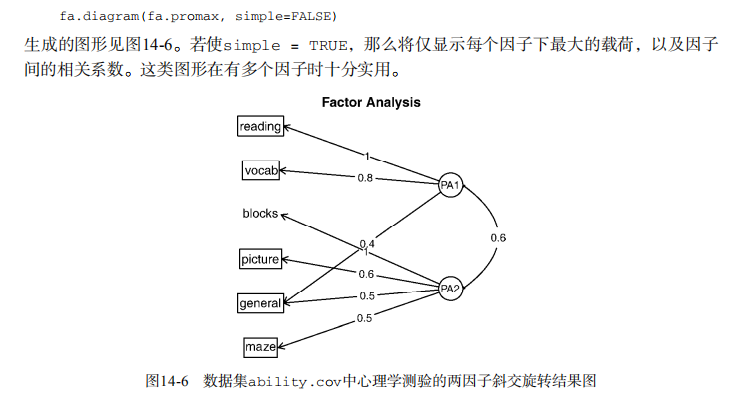
fa.diagram(fa.promax, simple=FALSE)
 
# factor scores
fa.promax$weights