RANSAC随机一致性采样算法学习体会

The RANSAC algorithm is a learning technique to estimate parameters of a model by random sampling of observed data. Given a dataset whose data elements contain both inliers and outliers, RANSAC uses the voting scheme to find the optimal fitting result. Data elements in the dataset are used to vote for one or multiple models. The implementation of this voting scheme is based on two assumptions: that the noisy features will not vote consistently for any single model (few outliers) and there are enough features to agree on a good model (few missing data). The RANSAC algorithm is essentially composed of two steps that are iteratively repeated:

1. In the first step, a sample subset containing minimal data items is randomly selected from the input dataset. A fitting model and the corresponding model parameters are computed using only the elements of this sample subset. The cardinality of the sample subset is the smallest sufficient to determine the model parameters.首先从输入数据中采集最小数据集，根据这个最小数据集计算相应的fitting模型参数。
2. In the second step, the algorithm checks which elements of the entire dataset are consistent with the model instantiated by the estimated model parameters obtained from the first step. A data element will be considered as an outlier if it does not fit the fitting model instantiated by the set of estimated model parameters within some error threshold that defines the maximum deviation attributable to the effect of noise.接着，应用第一步中得到的模型参数，检查整个输入数据集，如果和模型不匹配则视为离群点。通过一定的容错阈值范围限制由于噪声引起的最大误差，

The set of inliers obtained for the fitting model is called consensus set.适用模型的群内点被称为一致集。

The RANSAC algorithm will iteratively repeat the above two steps until the obtained consensus set in certain iteration has enough inliers.算法将重复上面的2个步骤进行迭代，直到通过一定迭代得到的一致集包含足够多的群内点。

The input to the RANSAC algorithm is a set of observed data values, a way of fitting some kind of model to the observations, and some confidence parameters. RANSAC achieves its goal by repeating the following steps:

1. Select a random subset of the original data. Call this subset the hypothetical inliers.
2. A model is fitted to the set of hypothetical inliers.//计算模型参数
3. All other data are then tested against the fitted model. Those points that fit the estimated model well, according to some model-specific loss function, are considered as part of the consensus set.
4. The estimated model is reasonably good if sufficiently many points have been classified as part of the consensus set.
5. Afterwards, the model may be improved by reestimating it using all members of the consensus set.

This procedure is repeated a fixed number of times, each time producing either a model which is rejected because too few points are part of the consensus set, or a refined model together with a corresponding consensus set size. In the latter case, we keep the refined model if its consensus set is larger than the previously saved model.

关于采样次数的推导

The values of parameters t and d have to be determined from specific requirements related to the application and the data set, possibly based on experimental evaluation. The parameter k (the number of iterations), however, can be determined from a theoretical result. Let p be the probability that the RANSAC algorithm in some iteration selects only inliers from the input data set when it chooses the n points from which the model parameters are estimated. When this happens, the resulting model is likely to be useful so p gives the probability that the algorithm produces a useful result. Let w be the probability of choosing an inlier each time a single point is selected, that is,

w = number of inliers in data / number of points in data

A common case is that w is not well known beforehand, but some rough value can be given. Assuming that the n points needed for estimating a model are selected independently, 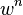 is the probability that all n points are inliers and  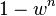is the probability that at least one of the n points is an outlier, a case which implies that a bad model will be estimated from this point set. That probability to the power of k is the probability that the algorithm never selects a set of n points which all are inliers and this must be the same as 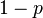. Consequently,

which, after taking the logarithm of both sides, leads to

This result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration. This is often not a reasonable approach and the derived value for k should be taken as an upper limit in the case that the points are selected without replacement. For example, in the case of finding a line which fits the data set illustrated in the above figure, the RANSAC algorithm typically chooses two points in each iteration and computes maybe_model as the line between the points and it is then critical that the two points are distinct.

To gain additional confidence, the standard deviation or multiples thereof can be added to k. The standard deviation of k is defined as