codevs4247奇特的生物 解析报告

4247 奇特的生物

时间限制: 1 s

空间限制: 128000 KB

题目等级 : 钻石 Diamond

题解

题目描述 Description

科学家们最近发现了一种奇怪的生物,它们每天长大一岁,刚出生的宝宝为1岁,且它们的年龄没有上限。已知年龄为1岁,2岁,3岁,……,k岁的个体具有生育能力,当年龄为i的具有生育能力的个体将长大一岁时会生下ai个1岁的幼崽。假设第一天只有一个年龄为1的幼崽,现在科学家们想知道第x天年龄为y的个体有多少,但由于该物种增长速度太快,于是他们将这个任务交给了你。由于这个数可能很大,你需要对p取模。

输入描述 Input Description

输入数据第一行给定四个整数k,x,y,p。

第二行包括k个整数,第i个整数代表ai。

输出描述 Output Description

输出数据包含一行,表示第x天年龄为y的个体的数量对p取模后的结果。

样例输入 Sample Input

【样例输入 1】

3 3 1 1007

1 1 1

【样例输入 2】

3 6 2 1007

1 2 1

样例输出 Sample Output

【样例输出1】

2

【样例输出 2】

13

增加一个新样例。codevs上的第十个点。

莫名其妙的矩阵快速幂解决不了。

样例输入3:

10 10258496531232 52 700000000017

5 89 63 25 48 76 95 23 15 25

样例输出3:

611559827774

分析：

这道题轻轻一想发现。哦。可以用递推来模拟。递推公式大致应该是这个样子的。

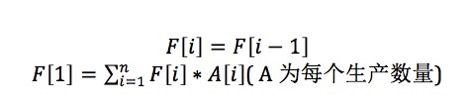
由题意可知。每个年龄的数量都是由上个年龄的人长成这个年龄的。而只有1岁的人是靠1-k有生育能力的人生产出来的。

由于这个范围很大。所以很容易让人想到用矩阵乘法来对这个进行递推优化。

但是仔细一想。发现这道题有个性质。就是没个人数都是由上一个转化过来的，那么。其实当F[1]产生的时候。以后的数量就是确定的。所以我们就没必要把全部的情况都存下来。就存1-k，每次进行状态转移就好。其次我们会发现。在整个序列里。因为只有F[1]在变所以我们求 x天y岁人数的问题就转换成了。我们求 x-y+1天1岁的人数问题。为什么呢？。我们y岁人数起时在底x-y+1天就转化好了。而之后剩下的天数，就是将x-y+1天1岁的人转移转移到x天y岁。

接下来的问题就剩到了，如何建立矩阵之后用矩阵来快速幂一些奇怪的事情。

这个矩阵很显然易见的解决这个问题。因为矩阵乘法是第一个举证的行乘第二个的列。所以我们在这里矩阵A第一行就是将F[1～k]里的所有结果相加。之后的行就完成了一个转移的工作。将上一天转换到当前天数。

于是就是将整个矩阵乘上 x-y 次。求A[1][1]－－代表第x－y＋1天的一岁的人数。

还有既然都是乘x－y次那么我们就要对（y>x）的情况进行特判。还有就是要加上快速乘法。不然第10个点过不去。这个数据就专门来卡你。

贴上代码。

#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
long long int mod,k,x,y;
struct node{
    long long l[100][100];
    node()
    {
	memset(l,0,sizeof(l));
    }
}a,ans;
long long  mul(long long x, long long y) {
    	long long  ret = 0;
	for(; y; y >>= 1) {
	    if((y & 1) && (ret += x) >= mod) ret -= mod;
	    if((x <<= 1) >= mod) x -= mod;
	}
	return ret;
}
node operator*(node a,node b)
{
        node res;
	for(int i=1;i<=k;++i)
	    for(int j=1;j<=k;++j)
	    {
	         for(int q=1;q<=k;++q)
		 {
		     res.l[i][j] += mul(a.l[i][q], b.l[q][j]);
		     if(res.l[i][j] >= mod) res.l[i][j] -= mod;
		 }
	    }
	    return res;
}
int main()
{
        scanf("%lld%lld%lld%lld",&k,&x,&y,&mod);
	for(long long int i=1;i<=k;++i)
	{
	     scanf("%lld",&a.l[1][i]);
	     a.l[i+1][i]=1;
	     ans.l[i][i]=1;
        }
	if(x<y){
		 printf("0");
	         return 0;
        }
        for(long long int i=x-y;i!=0;i>>=1 ,a=a*a)
	{
	     if(i&1)ans=a*ans;
	}
        printf("%lld",ans.l[1][1]);
	return 0;
}