EM算法——有隐含变量时，极大似然用梯度法搞不定只好来猜隐含变量期望值求max值了

摘自：https://www.zhihu.com/question/27976634

简单说一下为什么要用EM算法

现在一个班里有50个男生，50个女生，且男生站左，女生站右。我们假定男生的身高服从正态分布 ，女生的身高则服从另一个正态分布： 。这时候我们可以用极大似然法（MLE），分别通过这50个男生和50个女生的样本来估计这两个正态分布的参数。

但现在我们让情况复杂一点，就是这50个男生和50个女生混在一起了。我们拥有100个人的身高数据，却不知道这100个人每一个是男生还是女生。

这时候情况就有点尴尬，因为通常来说，我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。但从另一方面去考量，我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。

这个时候有人就想到我们必须从某一点开始，并用迭代的办法去解决这个问题：我们先设定男生身高和女生身高分布的几个参数（初始值），然后根据这些参数去判断每一个样本（人）是男生还是女生，之后根据标注后的样本再反过来重新估计参数。之后再多次重复这个过程，直至稳定。这个算法也就是EM算法。

为什么要用EM算法？

一般我们要利用一个最大似然法求（MLE）一个最大似然概率，那么问题来了，对原函数的MLE很可能求不出（函数太复杂，数据缺失等）。因为数据缺失而不能直接使用MLE方法的时候，我们可以用这个缺失数据的期望值来代替缺失的数据，而这个缺失的数据期望值和它的概率分布有关。那么我们可以通过对似然函数关于缺失数据期望的最大化，来逼近原函数的极大值（数学证明复杂），所以EM的两个步骤也是很明显了。

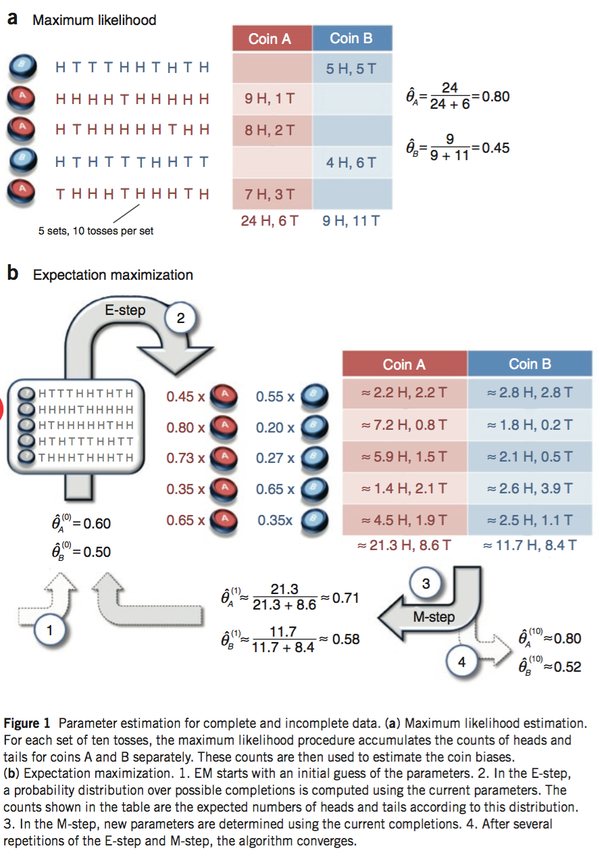
推一篇Nature Biotech的EM tutorial文章，用了一个投硬币的例子来讲EM算法的思想。

Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm?. Nature biotechnology, 26(8), 897.

现在有两个硬币A和B，要估计的参数是它们各自翻正面（head）的概率。观察的过程是先随机选A或者B，然后扔10次。以上步骤重复5次。

如果知道每次选的是A还是B，那可以直接估计（见下图a）。如果不知道选的是A还是B（隐变量），只观测到5次循环共50次投币的结果，这时就没法直接估计A和B的正面概率。EM算法此时可起作用（见下图b）。

推荐读原文，没有复杂的数学公式，通俗易懂。

摘自：http://blog.csdn.net/zouxy09/article/details/8537620

EM算法另一种理解

坐标上升法（Coordinate ascent）：

图中的直线式迭代优化的路径，可以看到每一步都会向最优值前进一步，而且前进路线是平行于坐标轴的，因为每一步只优化一个变量。

这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步：固定θ，优化Q；M步：固定Q，优化θ；交替将极值推向最大。