Python求阴影部分面积
一、前言说明
今天看到微信群里一道六年级数学题,如下图,求阴影部分面积
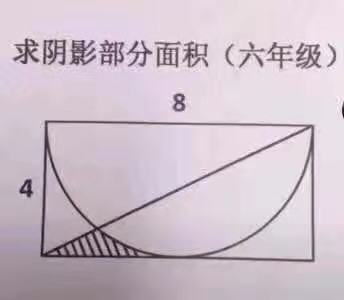
看起来似乎并不是很难,可是博主添加各种辅助线,写各种方法都没出来,不得已而改用写Python代码来求面积了
二、思路介绍
1.用Python将上图画在坐标轴上,主要是斜线函数和半圆函数
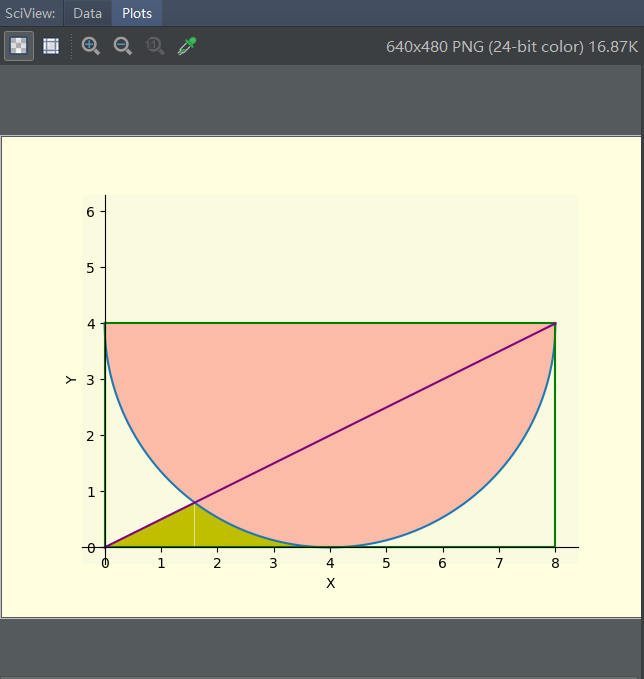
2.均匀的在长方形上面洒满豆子(假设是豆子),求阴影部分豆子占比*总面积
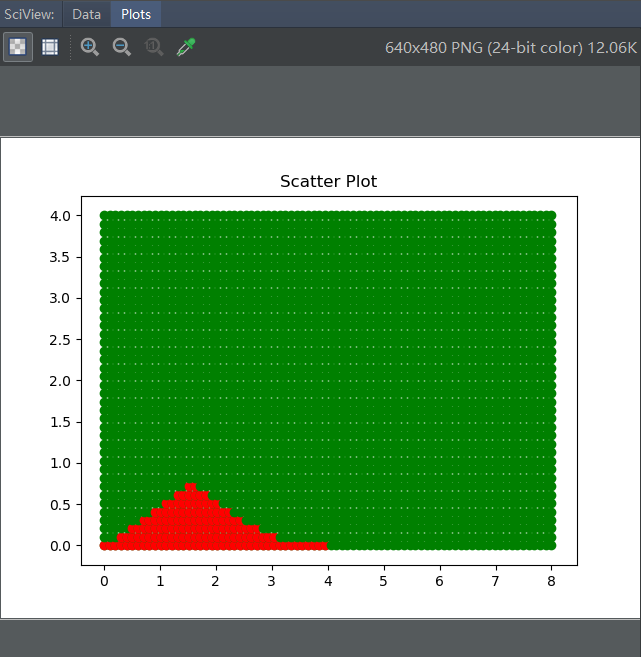
三、源码设计
1.做图源码
import matplotlib.pyplot as plt
import numpy as np def init():
plt.xlabel('X')
plt.ylabel('Y') fig = plt.gcf()
fig.set_facecolor('lightyellow')
fig.set_edgecolor("black") ax = plt.gca()
ax.patch.set_facecolor("lightgray") # 设置ax区域背景颜色
ax.patch.set_alpha(0.1) # 设置ax区域背景颜色透明度
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0)) # 原下半函数
def f1(px, r, a, b):
return b - np.sqrt(r**2 - (px - a)**2) # 斜线函数
def f2(px, m, n):
return px*n/m # 斜线函数2
def f3(px, m, n):
return n-1*px*n/m if __name__ == '__main__':
r = 4 # 圆半径
m = 8 # 宽
n = 4 # 高
a, b = (4, 4) # 圆心坐标
init() x = np.linspace(0, m, 100*m)
y = np.linspace(0, n, 100*n) # 半圆形
y1 = f1(x, r, a, b)
plt.plot(x, y1)
# 矩形横线
plt.plot((x.min(), x.max()), (y.min(), y.min()), 'g')
plt.plot((x.min(), x.max()), (y.max(), y.max()), 'g')
plt.plot((x.max(), x.max()), (y.max()+2, y.max()+2), 'g') # 画点(8,6)避免图形变形
# 矩形纵向
plt.plot((x.min(), x.min()), (y.min(), y.max()), 'g')
plt.plot((x.max(), x.max()), (y.min(), y.max()), 'g')
# 斜线方法
y2 = f2(x, m, n)
plt.plot(x, y2, 'purple') # 阴影部分填充
xf = x[np.where(x <= 0.5*x.max())]
plt.fill_between(xf, y.min(), f1(xf, r, a, b), where=f1(xf, r, a, b) <= f2(xf, m, n),
facecolor='y', interpolate=True)
plt.fill_between(xf, y.min(), f2(xf, m, n), where=f1(xf, r, a, b) > f2(xf, m, n),
facecolor='y', interpolate=True)
# 半圆填充
plt.fill_between(x, y1, y.max(), facecolor='r', alpha=0.25)
plt.show()
Draw.py
2.计算源码,其中side是要不要计算图形边框上的点,理论上side只能为True;t设置越大运行时间越长也越精准
import numpy as np def f1(px, r, a, b):
return b - np.sqrt(r**2 - (px - a)**2) def f2(px, m, n):
return px*n/m if __name__ == '__main__':
r = 4 # 圆半径
m = 8 # 宽
n = 4 # 高
a, b = (4, 4) # 圆心坐标
t = 100 # 精度 xs = np.linspace(0, m, 2*t*m)
ys = np.linspace(0, n, t*n) # 半圆形
y1 = f1(xs, r, a, b)
# 斜线
y2 = f2(xs, m, n) numin = 0
numtotel = 0
side = True # 是否计算边框
for x in xs:
for y in ys:
if not side:
if (x <= 0) | (x >= 8) | (y <= 0) | (y >= 4):
continue
numtotel += 1
if x >= 4:
continue
y1 = f1(x, r, a, b)
y2 = f2(x, m, n)
if y1 - y2 >= 0:
if y2 - y > 0:
numin += 1
if (y2 - y == 0) and side:
numin += 1
elif y2 - y1 > 0:
if y1 - y > 0:
numin += 1
if (y2 - y == 0) and side:
numin += 1 print(32*numin/numtotel)
calc.py
四、最后小结
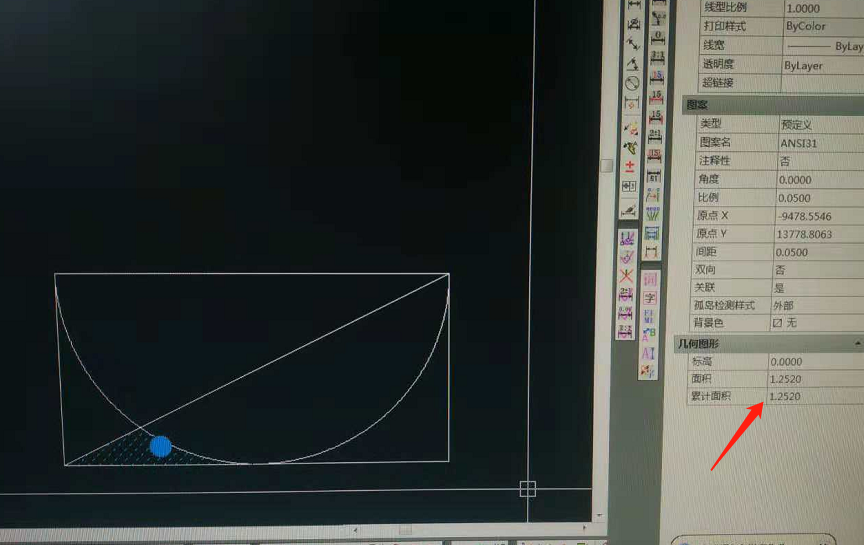
1.此种算法t为100时,阴影面积为1.268;t为1000时,阴影面积为1.253,已经非常接近正确答案(正确答案1.252)
2.举一反三,类似于这种不规则的面积,只要可以写出来函数,就可以求解面积.
2.下面有三种求解方法,第三种表示比大学高数还难看懂,你们呢?
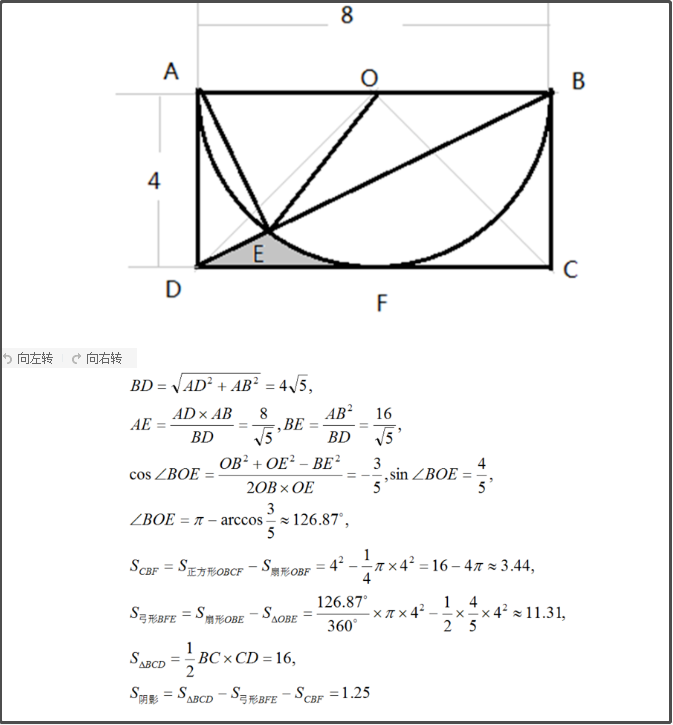
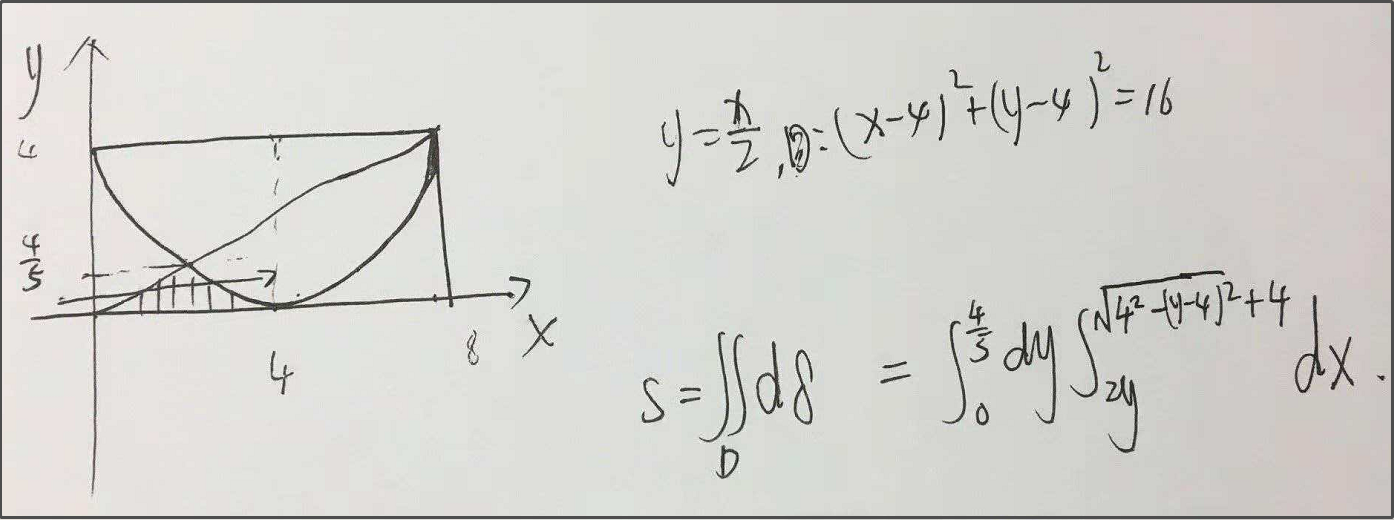
Python求阴影部分面积的更多相关文章
- TOJ 4701 求阴影部分面积
4701: 求阴影部分面积 本文版权归BobHuang和博客园共有,不得转载.如想转载,请联系作者,并注明出处. Time Limit(Common/Java):1000MS/3000MS ...
- 微信群里一道六年级数学题,求阴影面积,那我只能用python代码了
前言 文的文字及图片来源于网络,仅供学习.交流使用,不具有任何商业用途,版权归原作者所有,如有问题请及时联系我们以作处理. PS:如有需要Python学习资料的小伙伴可以加点击下方链接自行获取http ...
- 25.按要求编写一个Java应用程序: (1)编写一个矩形类Rect,包含: 两个属性:矩形的宽width;矩形的高height。 两个构造方法: 1.一个带有两个参数的构造方法,用于将width和height属性初化; 2.一个不带参数的构造方法,将矩形初始化为宽和高都为10。 两个方法: 求矩形面积的方法area() 求矩形周长的方法perimeter() (2)通过继承Rect类编写一个具有
package zhongqiuzuoye; //自己写的方法 public class Rect { public double width; public double height; Rect( ...
- POJ 1151 / HDU 1542 Atlantis 线段树求矩形面积并
题意:给出矩形两对角点坐标,求矩形面积并. 解法:线段树+离散化. 每加入一个矩形,将两个y值加入yy数组以待离散化,将左边界cover值置为1,右边界置为2,离散后建立的线段树其实是以y值建的树,线 ...
- UVa 11437:Triangle Fun(计算几何综合应用,求直线交点,向量运算,求三角形面积)
Problem ATriangle Fun Input: Standard Input Output: Standard Output In the picture below you can see ...
- hdu 1542 扫描线求矩形面积的并
很久没做线段树了 求矩形面积的并分析:1.矩形比较多,坐标也很大,所以横坐标需要离散化(纵坐标不需要),熟悉离散化后这个步骤不难,所以这里不详细讲解了,不明白的还请百度2.重点:扫描线法:假想有一条扫 ...
- 三角剖分求多边形面积的交 HDU3060
//三角剖分求多边形面积的交 HDU3060 #include <iostream> #include <cstdio> #include <cstring> #i ...
- Art Gallery - POJ 1279(求内核面积)
同上面几道题差不多,需要先求出来内核,然后直接用叉积求出来面积即可. 代码如下: #include<iostream> #include<string.h> #include& ...
- Area - POJ 1654(求多边形面积)
题目大意:从原点开始,1-4分别代表,向右下走,向右走,向右上走,向下走,5代表回到原点,6-9代表,向上走,向左下走,向左走,向左上走.求出最后的多边形面积. 分析:这个多边形面积很明显是不规则的, ...
随机推荐
- IOS - 退出程序
- (void)exitApplication { OAAppDelegate *app = [UIApplication sharedApplication].delegate; UIWindow ...
- windows下Word使用-快捷键
1.word全屏显示——Alt+U+V 2.上标——Ctrl+Shift+= 3.下标——Ctrl+=
- CRM系统 - 总结 (一) 权限
1. 问:为什么程序需要权限控制? 答:生活中的权限限制,① 看灾难片电影<2012>中富人和权贵有权登上诺亚方舟,穷苦老百姓只有等着灾难的来临:② 屌丝们,有没有想过为什么那些长得漂亮身 ...
- 监控myserver计数器
- Springboot 应用启动分析
https://blog.csdn.net/hengyunabc/article/details/50120001#comments 一,spring boot quick start 在spring ...
- mysql5.7官网直译SQL语句优化--select语句优化
8.2 sql语句优化 大致内容如下: 8.2.1:SELECT语句的优化 8.2.2:优化子查询,派生表和试图引用 8.2.3:优化INFORMATION_SCHEMA查询 8.2.4:优化数据改变 ...
- Ruby print
Ruby print
- Excel数据导入___你hold住么(一)
近期小编跟着团队一起开发ITOO3.0高校云平台项目,当中的收获是不言而喻滴,在项目中有个导入功能:导入学生信息:导入班级信息:导入教学楼信息等,在不知多少次的尝试之下,成功实现功能. 框架分析 详解 ...
- UVA 1329 Corporative Network【并查集】
题目链接: https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_proble ...
- nyist oj 138 找球号(二)(hash 表+位运算)
找球号(二) 时间限制:1000 ms | 内存限制:65535 KB 难度:5 描写叙述 在某一国度里流行着一种游戏.游戏规则为:现有一堆球中.每一个球上都有一个整数编号i(0<=i< ...
