AVL树的实现例程

/* AVL树的节点声明 */

#ifndef _AVLTREE_H
#define _AVLTREE_H

struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;

AvlTree MakeEmpty(AvlTree T);
Position Find(ElementType X, AvlTree T);
Position FindMin(AvlTree T);
Position FindMax(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
AvlTree Delete(ElementType X, AvlTree T);
ElementType Retrieve(Position P);

#endif    /* _AVLTREE_H */

/* Place in the implementation file */
struct AvlNode
{
    ElementType Element;
    AvlTree Left;
    AvlTree Right;
    int Height;
};

/* 计算AVL节点的高度 */

static int
Height(Position P)
{
    if(P == NULL)
        return -1;
    else
        return P->Height;
}

/* 向AVL树插入节点的例程 */

AvlTree
Insert(ElementType X, AvlTree T)
{
    if(T == NULL)
    {
        /* Create and return a one-node tree */
        T = malloc(sizeof(struct AvlNode));
        if(T == NULL)
            FatalError("Out of space!!!");
        else
        {
            T->Element = X;
            T->Height = 0;
            T->Left = NULL;
            T->Right = NULL;
        }
    }
    else if(X < T->Element)
    {
        T->Left = Insert(X, T->Left);
        if(Height(T->Left) - Height(T->Right) == 2)
        {
            if(X < T->Left->Element)
                T = SingleRotateWithLeft(T);
            else
                T = DoubleRotateWithLeft(T);
        }
    }
    else if(X > T->Element)
    {
        T->Right = Insert(X, T->Right);
        if(Height(T->Right) - Height(T->Left) == 2)
        {
            if(X > T->Right->Element)
                T = SingleRotateWithRight(T);
            else
                T = DoubleRotateWithRight(T);
        }
    }
    /* Else X is in the tree already; we'll do nothing */

    T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
    return T;
}

/* 执行单旋转的例程 */

static Postition
SingleRotateWithLeft(Position K2)
{
    Position K1;
    K1 = K2->left;
    K2->Left = K1->Right;
    K1->Right = K2;

    K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
    K1->Height = Max(Height(K1->Left), Height(K1->Left)) + 1;

    return K1;        /* New root */
}

/* 执行双旋转的例程 */

static Position
DoubleRotateWithLeft(Position K3)
{
    /* Rotate between K1 and K2 */
    K3->Left = SingleRotateWithLeft(K3->Left);

    /* Rotate between K3 and K2 */
    return SingleRotateWithLeft(K3);
}

附图：

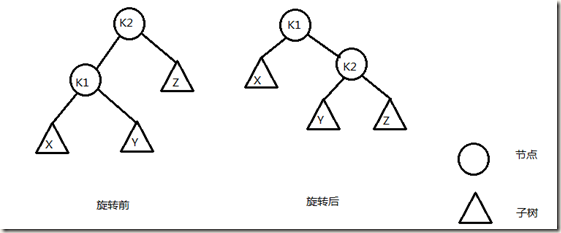
                                                     单旋转

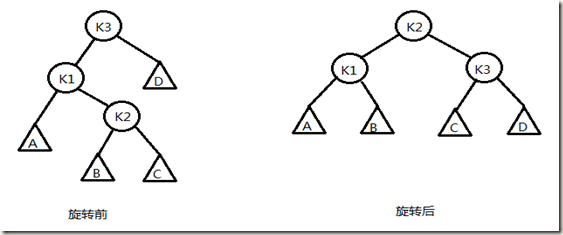
                                                     双旋转