伸展树的实现——c++

 一、介绍

伸展树(Splay Tree)是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。
(01) 伸展树属于二叉查找树，即它具有和二叉查找树一样的性质：假设x为树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。
(02) 除了拥有二叉查找树的性质之外，伸展树还具有的一个特点是：当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。

假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法，在每次查找之后对树进行重构，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生，它是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

相比于"二叉查找树"和"AVL树"，学习伸展树时需要重点关注是"伸展树的旋转算法"。

二、伸展树的c++实现

1. 基本定义

1.1 节点

template <class T>
class SplayTreeNode{
    public:
        T key;                // 关键字(键值)
        SplayTreeNode *left;    // 左孩子
        SplayTreeNode *right;    // 右孩子

        SplayTreeNode():left(NULL),right(NULL) {}

        SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r):
            key(value), left(l),right(r) {}
};

SplayTreeNode是伸展树节点对应的类。它包括的几个组成元素:
(01) key -- 是关键字，是用来对伸展树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。

1.2 伸展树

template <class T>
class SplayTree {
    private:
        SplayTreeNode<T> *mRoot;    // 根结点

    public:
        SplayTree();
        ~SplayTree();

        // 前序遍历"伸展树"
        void preOrder();
        // 中序遍历"伸展树"
        void inOrder();
        // 后序遍历"伸展树"
        void postOrder();

        // (递归实现)查找"伸展树"中键值为key的节点
        SplayTreeNode<T>* search(T key);
        // (非递归实现)查找"伸展树"中键值为key的节点
        SplayTreeNode<T>* iterativeSearch(T key);

        // 查找最小结点：返回最小结点的键值。
        T minimum();
        // 查找最大结点：返回最大结点的键值。
        T maximum();

        // 旋转key对应的节点为根节点，并返回值为根节点。
        void splay(T key);

        // 将结点(key为节点键值)插入到伸展树中
        void insert(T key);

        // 删除结点(key为节点键值)
        void remove(T key);

        // 销毁伸展树
        void destroy();

        // 打印伸展树
        void print();
    private:

        // 前序遍历"伸展树"
        void preOrder(SplayTreeNode<T>* tree) const;
        // 中序遍历"伸展树"
        void inOrder(SplayTreeNode<T>* tree) const;
        // 后序遍历"伸展树"
        void postOrder(SplayTreeNode<T>* tree) const;

        // (递归实现)查找"伸展树x"中键值为key的节点
        SplayTreeNode<T>* search(SplayTreeNode<T>* x, T key) const;
        // (非递归实现)查找"伸展树x"中键值为key的节点
        SplayTreeNode<T>* iterativeSearch(SplayTreeNode<T>* x, T key) const;

        // 查找最小结点：返回tree为根结点的伸展树的最小结点。
        SplayTreeNode<T>* minimum(SplayTreeNode<T>* tree);
        // 查找最大结点：返回tree为根结点的伸展树的最大结点。
        SplayTreeNode<T>* maximum(SplayTreeNode<T>* tree);

        // 旋转key对应的节点为根节点，并返回值为根节点。
        SplayTreeNode<T>* splay(SplayTreeNode<T>* tree, T key);

        // 将结点(z)插入到伸展树(tree)中
        SplayTreeNode<T>* insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z);

        // 删除伸展树(tree)中的结点(键值为key)，并返回被删除的结点
        SplayTreeNode<T>* remove(SplayTreeNode<T>* &tree, T key);

        // 销毁伸展树
        void destroy(SplayTreeNode<T>* &tree);

        // 打印伸展树
        void print(SplayTreeNode<T>* tree, T key, int direction);
};

playTree是伸展树对应的类。它包括根节点mRoot和伸展树的函数接口。

2. 旋转（重点）

/*
 * 旋转key对应的节点为根节点，并返回值为根节点。
 *
 * 注意：
 *   (a)：伸展树中存在"键值为key的节点"。
 *          将"键值为key的节点"旋转为根节点。
 *   (b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
 *      b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
 *      b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
 *   (c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
 *      c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
 *      c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
 */
template <class T>
SplayTreeNode<T>* SplayTree<T>::splay(SplayTreeNode<T>* tree, T key)
{
    SplayTreeNode<T> N, *l, *r, *c;

    if (tree == NULL)
        return tree;

    N.left = N.right = NULL;
    l = r = &N;

    for (;;)
    {
        if (key < tree->key)
        {
            if (tree->left == NULL)
                break;
            if (key < tree->left->key)
            {
                c = tree->left;                           /* rotate right */
                tree->left = c->right;
                c->right = tree;
                tree = c;
                if (tree->left == NULL)
                    break;
            }
            r->left = tree;                               /* link right */
            r = tree;
            tree = tree->left;
        }
        else if (key > tree->key)
        {
            if (tree->right == NULL)
                break;
            if (key > tree->right->key)
            {
                c = tree->right;                          /* rotate left */
                tree->right = c->left;
                c->left = tree;
                tree = c;
                if (tree->right == NULL)
                    break;
            }
            l->right = tree;                              /* link left */
            l = tree;
            tree = tree->right;
        }
        else
        {
            break;
        }
    }

    l->right = tree->left;                                /* assemble */
    r->left = tree->right;
    tree->left = N.right;
    tree->right = N.left;

    return tree;
}

template <class T>
void SplayTree<T>::splay(T key)
{
    mRoot = splay(mRoot, key);
}

上面的代码的作用：将"键值为key的节点"旋转为根节点，并返回根节点。它的处理情况共包括：
(a)：伸展树中存在"键值为key的节点"。
        将"键值为key的节点"旋转为根节点。
(b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
        b-1) "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
        b-2) "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
(c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
        c-1) "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
        c-2) "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。

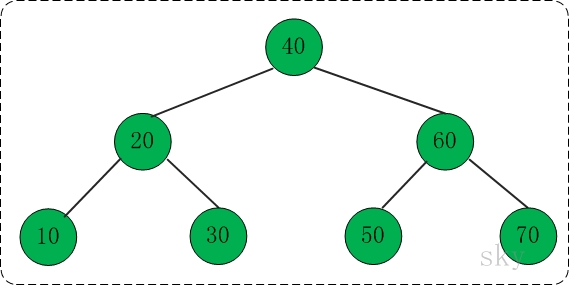
下面列举个例子分别对a进行说明。

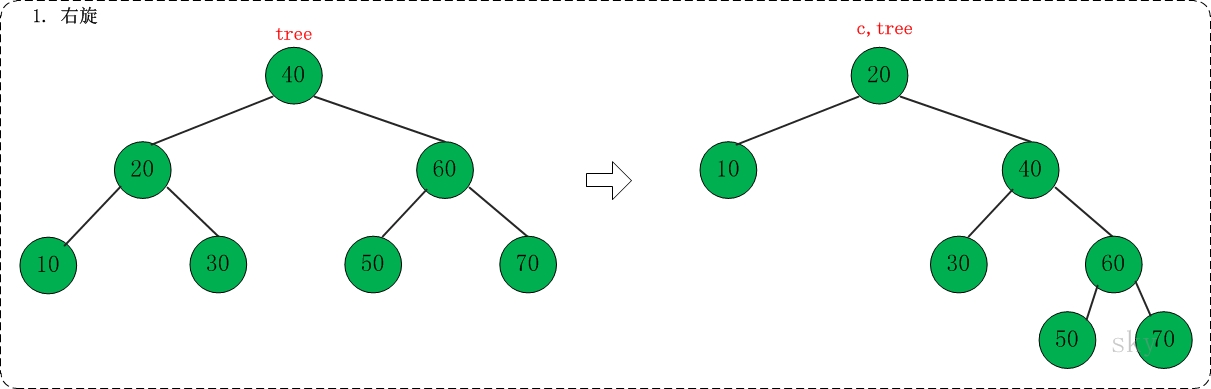
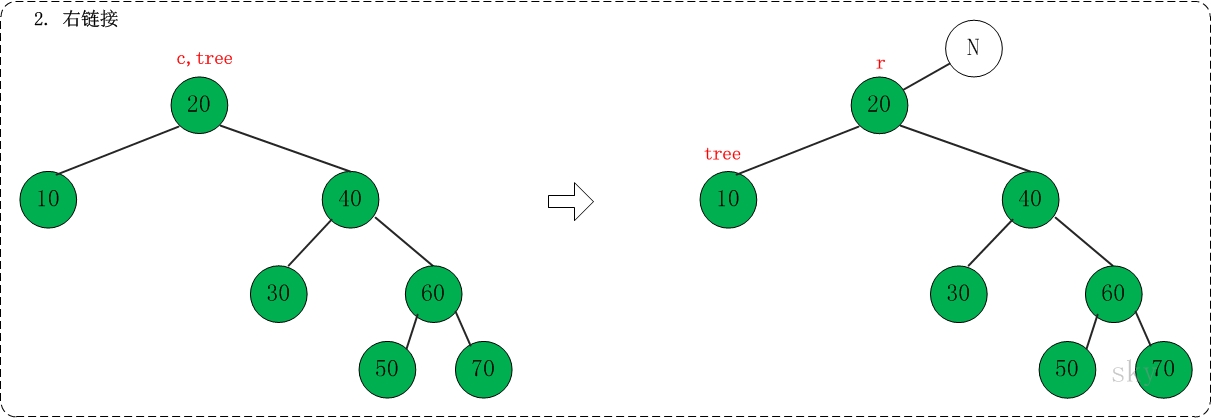
在下面的伸展树中查找10，共包括"右旋" --> "右链接" --> "组合"这3步。

(01) 右旋
对应代码中的"rotate right"部分

(02) 右链接
对应代码中的"link right"部分

(03) 组合
对应代码中的"assemble"部分

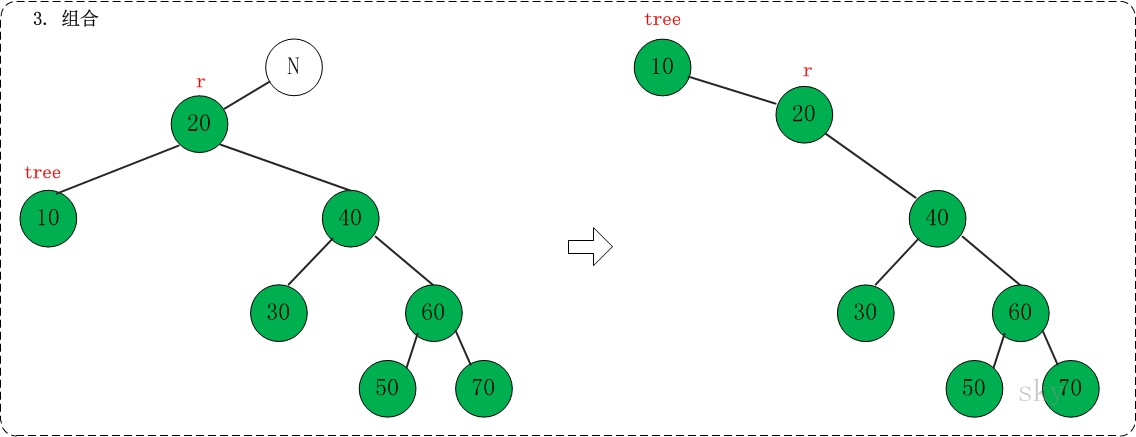
提示：如果在上面的伸展树中查找"70"，则正好与"示例1"对称，而对应的操作则分别是"rotate left", "link left"和"assemble"。
其它的情况，例如"查找15是b-1的情况，查找5是b-2的情况"等等，这些都比较简单，大家可以自己分析。

3. 插入节点

/*
 * 将结点插入到伸展树中，并返回根节点
 *
 * 参数说明：
 *     tree 伸展树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
template <class T>
SplayTreeNode<T>* SplayTree<T>::insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z)
{
    SplayTreeNode<T> *y = NULL;
    SplayTreeNode<T> *x = tree;

    // 查找z的插入位置
    while (x != NULL)
    {
        y = x;
        if (z->key < x->key)
            x = x->left;
        else if (z->key > x->key)
            x = x->right;
        else
        {
            cout << "不允许插入相同节点(" << z->key << ")!" << endl;
            delete z;
            return tree;
        }
    }

    if (y==NULL)
        tree = z;
    else if (z->key < y->key)
        y->left = z;
    else
        y->right = z;

    return tree;
}

template <class T>
void SplayTree<T>::insert(T key)
{
    SplayTreeNode<T> *z=NULL;

    // 如果新建结点失败，则返回。
    if ((z=new SplayTreeNode<T>(key,NULL,NULL)) == NULL)
        return ;

    // 插入节点
    mRoot = insert(mRoot, z);
    // 将节点(key)旋转为根节点
    mRoot = splay(mRoot, key);
}

4. 删除节点

/*
 * 删除结点(节点的键值为key)，返回根节点
 *
 * 参数说明：
 *     tree 伸展树的根结点
 *     key 待删除结点的键值
 * 返回值：
 *     根节点
 */
template <class T>
SplayTreeNode<T>* SplayTree<T>::remove(SplayTreeNode<T>* &tree, T key)
{
    SplayTreeNode<T> *x;

    if (tree == NULL)
        return NULL;

    // 查找键值为key的节点，找不到的话直接返回。
    if (search(tree, key) == NULL)
        return tree;

    // 将key对应的节点旋转为根节点。
    tree = splay(tree, key);

    if (tree->left != NULL)
    {
        // 将"tree的前驱节点"旋转为根节点
        x = splay(tree->left, key);
        // 移除tree节点
        x->right = tree->right;
    }
    else
        x = tree->right;

    delete tree;

    return x;

}

template <class T>
void SplayTree<T>::remove(T key)
{
    mRoot = remove(mRoot, key);
}

remove(key)是外部接口，remove(tree, key)是内部接口。
remove(tree, key)的作用是：删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话，则直接返回。若找到的话，则将该节点旋转为根节点，然后再删除该节点。

本文来自http://www.cnblogs.com/skywang12345/p/3604238.html