线性分类中的是非题------>概率题，
设置概率阈值后，大于等于该值的为O，小于改值的为X。------>逻辑回归。
O为1，X为0：
逻辑回归假设：
逻辑函数/S型函数：光滑，单调，
自变量趋于负无穷时，因变量趋于0；
自变量趋于正无穷时，因变量趋于1；
自变量取0时，因变量值为0.5。
－－－模拟概率特性。
三种线性模型：
逻辑回归使用交叉熵代价函数。
最小化代价函数时，
发现无法求出使其值最小的解析解，
类比PLA的迭代法，使用梯度下降法求最小值。
 
eta------学习速率，与梯度大小有关，正比。
v------方向，单位长度，方向与梯度相反。

逻辑回归算法流程：

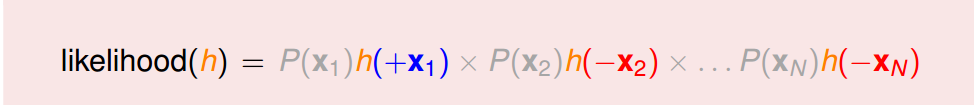
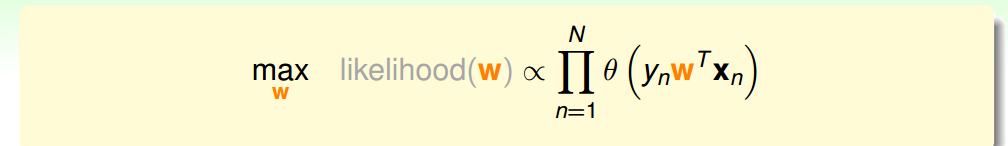
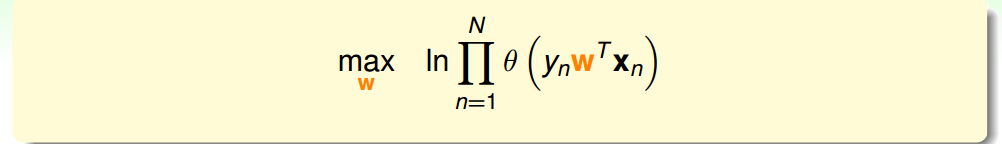
机器学习基石笔记：10 Logistic Regression的更多相关文章

  1. 机器学习基石：10 Logistic Regression

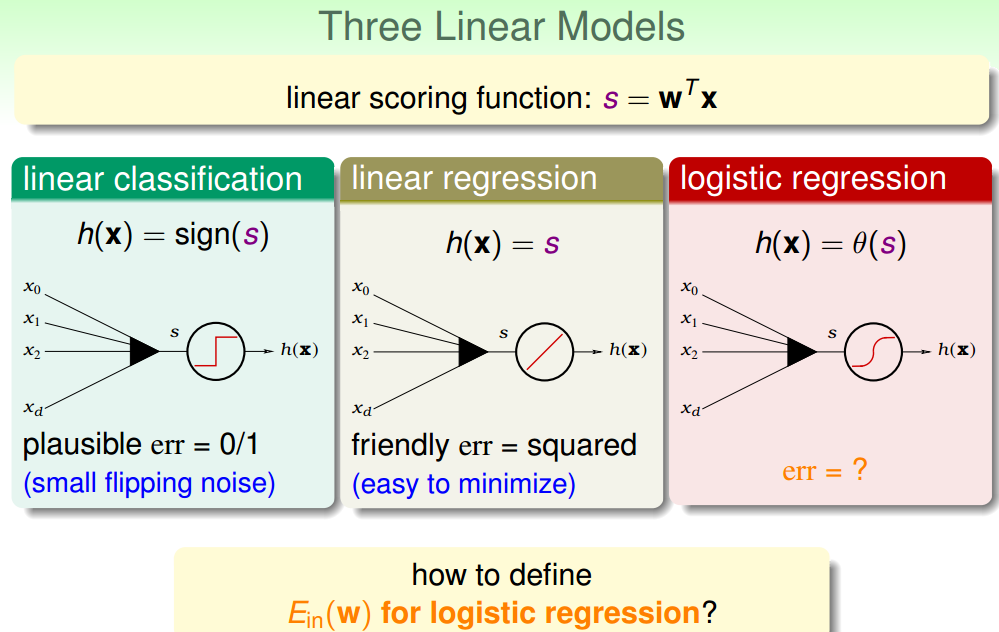
    线性分类中的是非题------>概率题, 设置概率阈值后,大于等于该值的为O,小于改值的为X.------>逻辑回归. O为1,X为0: 逻辑回归假设: 逻辑函数/S型函数:光滑,单调, ...

  2. Coursera台大机器学习课程笔记9 -- Logistic Regression

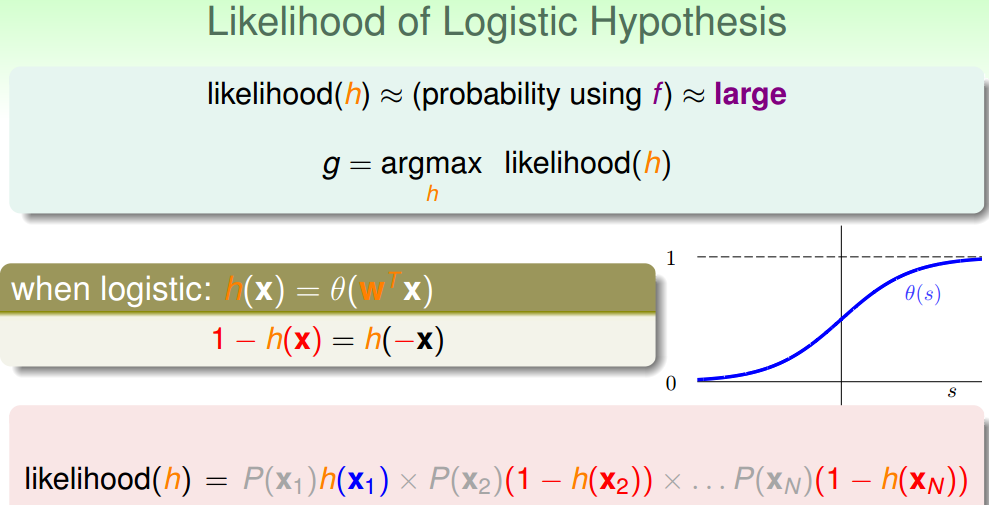
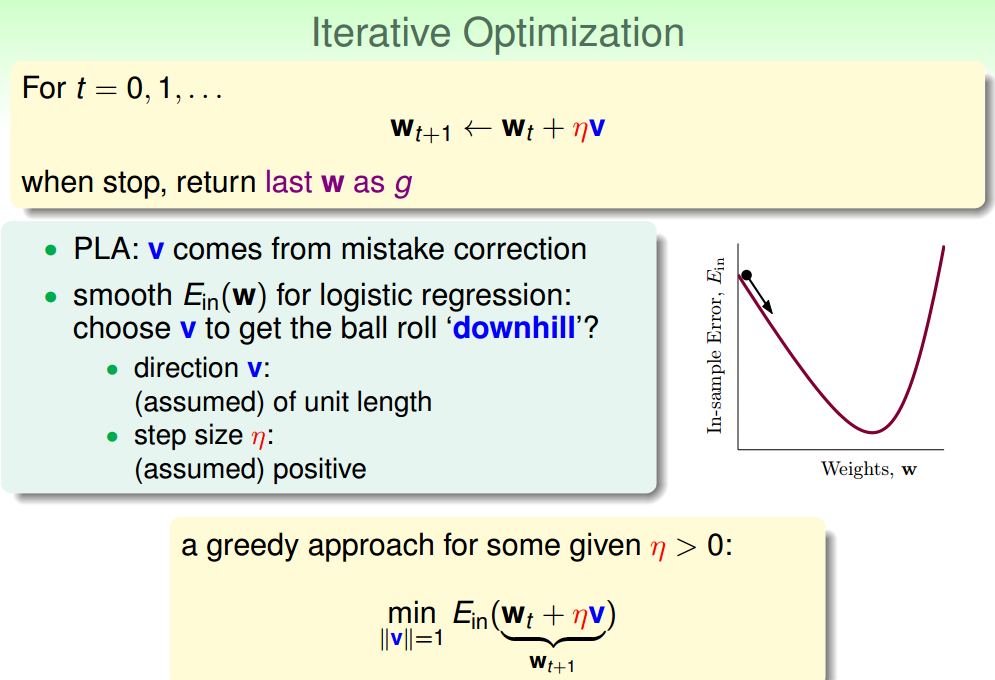
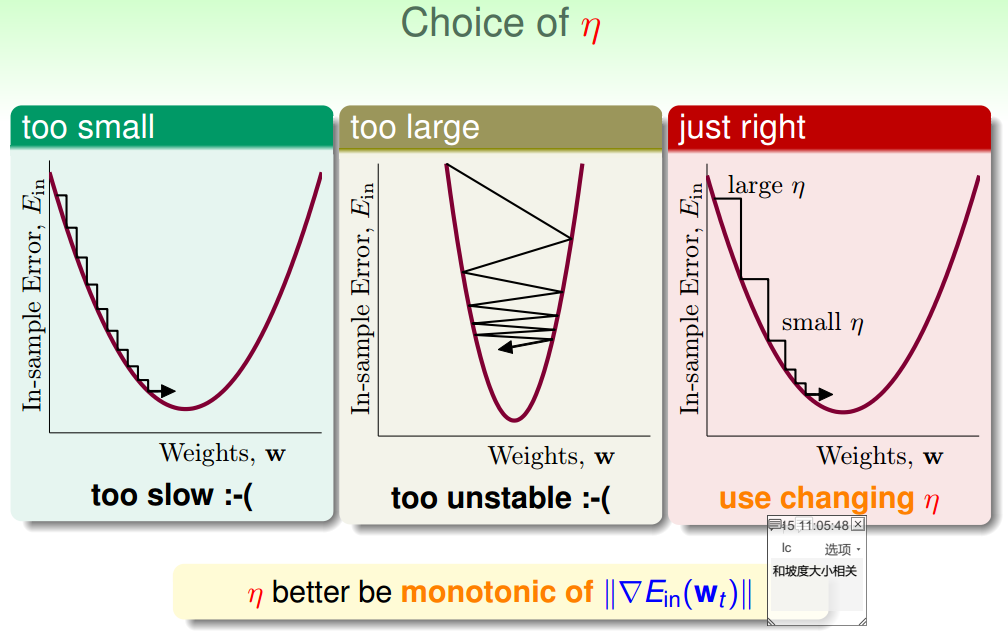
    如果只想得到某种概率,而不是简单的分类,那么该如何做呢?在误差衡量问题上,如何选取误差函数这段很有意思. 接下来是如何最小化Ein,由于Ein是可凸优化的,所以采用的是梯度下降法:只要达到谷底,就找到 ...

  3. Stanford机器学习笔记-2.Logistic Regression

    Content: 2 Logistic Regression. 2.1 Classification. 2.2 Hypothesis representation. 2.2.1 Interpretin ...

  4. Coursera台大机器学习技法课程笔记05-Kernel Logistic Regression

    这一节主要讲的是如何将Kernel trick 用到 logistic regression上. 从另一个角度来看soft-margin SVM,将其与 logistic regression进行对比 ...

  5. 机器学习/逻辑回归（logistic regression）/--附python代码

    个人分类: 机器学习 本文为吴恩达<机器学习>课程的读书笔记,并用python实现. 前一篇讲了线性回归,这一篇讲逻辑回归,有了上一篇的基础,这一篇的内容会显得比较简单. 逻辑回归(log ...

  6. 机器学习 (三) 逻辑回归 Logistic Regression

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...

  7. 机器学习之LinearRegression与Logistic Regression逻辑斯蒂回归(三)

    一 评价尺度 sklearn包含四种评价尺度 1 均方差(mean-squared-error) 2 平均绝对值误差(mean_absolute_error) 3 可释方差得分(explained_v ...

  8. 机器学习——逻辑回归（Logistic Regression）

    1 前言 虽然该机器学习算法名字里面有"回归",但是它其实是个分类算法.取名逻辑回归主要是因为是从线性回归转变而来的. logistic回归,又叫对数几率回归. 2 回归模型 2. ...

  9. Coursera台大机器学习课程笔记10 -- Linear Models for Classification

    这一节讲线性模型,先将几种线性模型进行了对比,通过转换误差函数来将linear regression 和logistic regression 用于分类. 比较重要的是这种图,它解释了为何可以用Lin ...

  10. 机器学习基石笔记：11 Linear Models for Classification

    一.二元分类的线性模型 线性分类.线性回归.逻辑回归: 可视化这三个线性模型的代价函数, SQR.SCE的值都是大于等于0/1的. 理论分析上界: 将回归应用于分类: 线性回归后的参数值常用于pla/ ...

随机推荐

  1. Linux命令行报错 bash: cannot create temp file for here-document: No space left on device

    今天Linux服务器出问题了,使用"tab"补全命令时,提示 bash: cannot create temp file for here-document: No space l ...

  2. Linux Oracle安装

    lsnrctl status  // 查看linux系统oracle的监听状态lsnrctl start   // 启动linux系统oracle的监听状态 sqlplus /nolog  // 连接 ...

  3. sessionStorage实现note的功能

    功能图如图所示: 文本域中输入点击保存后的结果如图所示: 点击读取后的结果图: 选择山羊对应的按钮进行修改并点击保存后的结果: 选择山羊养对应的单选按钮进行删除操作后的结果图: 点击清空后的结果: 源 ...

  4. vue 关键词模糊查询

    页面html,绑定的列表数据为datas,关键词为 select_words,如下图 其中d.accounts和d.roleName是需要进行搜索的字段,也可以进行大小写都可以

  5. 508. Most Frequent Subtree Sum 最频繁的子树和

    ［抄题］: Given the root of a tree, you are asked to find the most frequent subtree sum. The subtree sum ...

  6. [leetcode]94. Binary Tree Inorder Traversal二叉树中序遍历

    Given a binary tree, return the inorder traversal of its nodes' values. Example: Input: [1,null,2,3] ...

  7. ES6 proxy(代理拦截) &&Reflect

  8. Sonar+maven+jenkins集成，Java代码走查

    Sonar服务在Sonar安装与使用篇已经介绍过,此文章不再说了 Jenkins的安装与配置方法参考http://www.cnblogs.com/chenchen-tester/p/6408815.h ...

  9. 锻造(forging)

    --九校联考24OI__D1T1 题目背景 勇者虽然武力值很高,但在经历了多次战斗后,发现怪物越来越难打,于是开始思考是不是自己平时锻炼没到位,于是苦练一个月后发现--自己连一个史莱姆都打不过了. 勇 ...

  10. zeromq学习记录(四)使用ZMQ_ROUTER ZMQ_DEALER

    /************************************************************** 技术博客 http://www.cnblogs.com/itdef/   ...