光流法详解之二（HS光流）

Horn–Schunck光流算法[1]是一种全局方法估算光流场。

参考博文：https://blog.csdn.net/hhyh612/article/details/79216021

假设条件：

HS算法除了需要满足LK光流前两个假设之外，增加了一个假设条件：

　　场景中属于同一物体的像素形成光流场向量应当十分平滑，只有在物体边界的地方才会出现光流的突变，但这只占图像的一小部分，总体上来看图像的光流场应当是平滑的。

数学原理推导：

　 仍然是两帧图像I(x, y, t), 和I(x+δx, y+δy, z+δz, t+δt )。要求他们之间的光流场V(u, v):

　首先定义一个能量函数， 如下：

　　

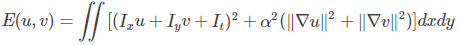
　　这个能量函数的前半部分是灰度变化因子，如下：

　　

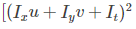
　　后半部分是平滑因子，如下：

　　

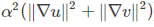
　　理想的光流场，应该使这两项的值最小：即灰度变化小（亮度恒定）并且速度变化小（小运动）。

　　这是一个泛函的极值问题，可以用欧拉-拉格朗日方程求解。对应上式的是双变量双函数一阶导数的欧拉-拉格朗日方程组

　　　　　　　　　　

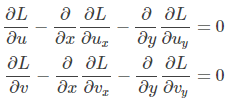
　　其中上式中：

　　　　

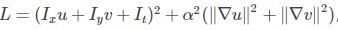
　　求导， 得到下式：

　　　　

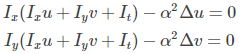
　　上式中Δ是拉普拉斯算子操作：

　　　　　　

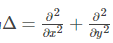
　　实际计算中可以用下面的式子代替拉普拉斯操作：

　　　　　　

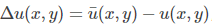
　　拉普拉斯操作替换后化简为下式：

　　　　　　

　　这是一个线性方程组，但是首先要求取u，v的均值，然而u, v的均值也是未知的，因此可以继续化简上式，分别消去u和v，得到下面的迭代公式：

　　　　　　　　 

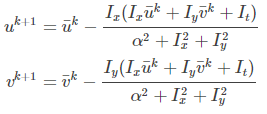
　　有了迭代公式后，u, v均值的初始值为0，计算出u, v值，然后依次迭代。直到满足如下条件，退出迭代，得到光流u, v值：

　　　　

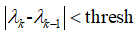
　　其中：

　　　　

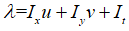
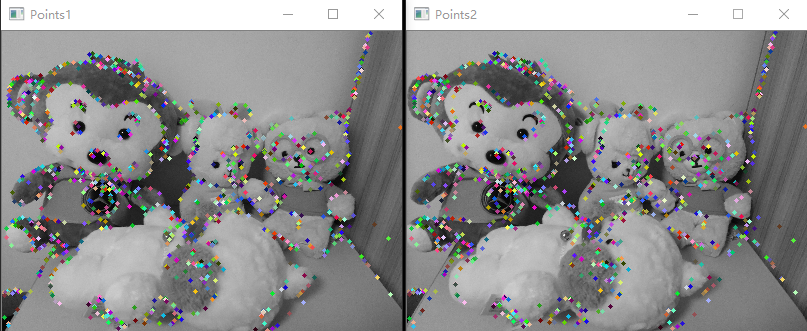
源码及效果：

　　源码链接：https://blog.csdn.net/xiaoyufei117122/article/details/53693627

　　效果如下：

　　

[1]  B.K.P. Horn and B.G. Schunck, “Determining optical flow.” 1981