转自：http://www.cnblogs.com/rocketfan/archive/2011/07/03/2096953.html

主要记录下几个文章博客内容

A Note on EM Algorithm for Probabilistic Latent SemanticAnalysis（翟成祥的NOTE）

A Note on EM Algorithm and PLSA（一个中文比较好的总结 by Xinyan Lu）

注意这两个是一个思路

Probabilistic Latent Semantic Analysis （原论文）

原论文是另一个思路

Notes on Probabilistic Latent Semantic Analysis (PLSA)（这个里面对比了两种不同思路，原论文与翟成祥NOTE，Xinyan Lu中文总结 分布对应这两种思路）

先看第一种思路，这个更好理解一点

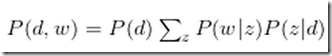
典型的EM算法 hidden/latent variable 是主题Z，p(d)对于我们的计算可忽略,最后面那个博客的总结证明更完整。

类似前面的混合高斯模型，这里实际Estep要估算的就是对应d,w 情况下Z的概率

Estep 对比前面高斯模型 具体一个观察点情况下对应到隐藏分类的概率

解释下 sum_z(p(z|d)p(w|z))= p(w|d)     p(d)p(w|d)p(z|d,w) = p(d,w,z)  => p(w|d)p(z|d,w) = p(d,w,z)/p(d) = p(w,z|d)=p(z|d)p(w|z)

=> p(z|w,d) = p(z|d)(pw|z) / p(w|d)

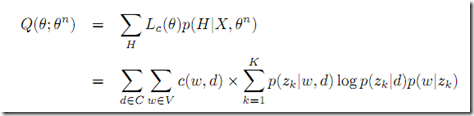
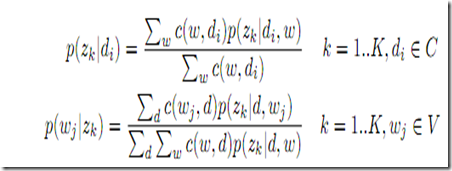Mstep

对比NG的课件

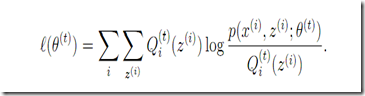
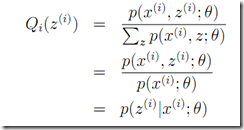x对应这里的w

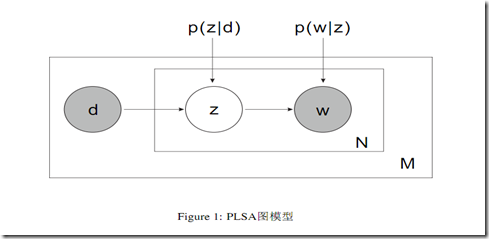
如果我们考虑背景噪音,翟成祥的NOTE更进一步给出了在这个基础上稍微复杂一点的MODLE和结果

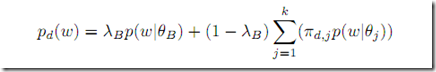考虑下翟成祥那篇EM中的简单混合模型

  topic Z

其实和上面公式一样  p(z|d)

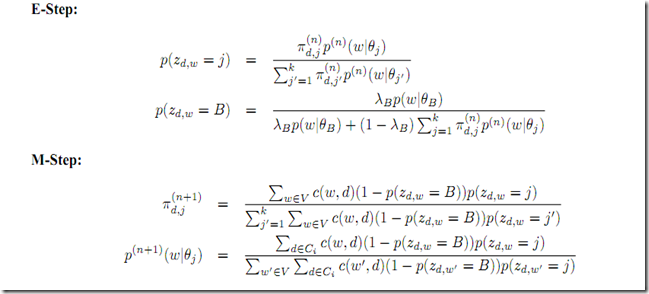
第二种思路

TODO

PLSA中的EM算法的更多相关文章

  1. 机器学习中的EM算法具体解释及R语言实例（1）

    最大期望算法(EM) K均值算法很easy(可參见之前公布的博文),相信读者都能够轻松地理解它. 但以下将要介绍的EM算法就要困难很多了.它与极大似然预计密切相关. 1 算法原理 最好还是从一个样例開 ...

  2. opencv3中的机器学习算法之：EM算法

    不同于其它的机器学习模型,EM算法是一种非监督的学习算法,它的输入数据事先不需要进行标注.相反,该算法从给定的样本集中,能计算出高斯混和参数的最大似然估计.也能得到每个样本对应的标注值,类似于kmea ...

  3. 机器学习-EM算法笔记

    EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域算法的基础,比如隐式马尔科夫算法(HMM), LDA主题模型的变分推断,混合高斯模型 ...

  4. 高斯混合和EM算法

    首先介绍高斯混合模型: 高斯混合模型是指具有以下形式的概率分布模型: 一般其他分布的混合模型用相应的概率密度代替(1)式中的高斯分布密度即可. 给定训练集,我们希望构建该数据联合分布 这里,其中是概率 ...

  5. EM算法及其推广的要点

    1.EM算法是含有隐变量的变量的概率模型极大似然估计或极大后验概率估计的迭代算法,含有隐变量的概率模型的数据表示为$P(Y,Z|\theta)$.这里,$Y$是观测变量的数据,$Z$是隐变量的数据,$ ...

  6. EM算法学习资料备忘

    将学习EM算法过程中看到的好的资料汇总在这里,供以后查询.也供大家參考. 1. 这是我学习EM算法最先看的优秀的入门文章,讲的比較通俗易懂,并且举了样例来说明当中的原理.不错! http://blog ...

  7. EM算法(Expectation Maximization Algorithm)

    EM算法(Expectation Maximization Algorithm) 1. 前言   这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...

  8. EM算法（expectation maximization）

    EM算法简述 EM算法是一种迭代算法,主要用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计.EM算法的每次迭代由两步完成: E步,求期望 M步,求极大. EM算法的引入 如果概率模型的变 ...

  9. PLSA及EM算法

    前言:本文主要介绍PLSA及EM算法,首先给出LSA(隐性语义分析)的早期方法SVD,然后引入基于概率的PLSA模型,其参数学习采用EM算法.接着我们分析如何运用EM算法估计一个简单的mixture ...

随机推荐

  1. php 获取301 302的真实地址

    function getRealURL($url){ $header = get_headers($url,1); if (strpos($header[0],'301') || strpos($he ...

  2. ecshop 文章列表页调用描述信息啊

    1.打开 includes/lib_article.php文件 将 $sql = 'SELECT article_id, title, author, add_time, file_url, open ...

  3. （六）6.18 cnn 的反向传导算法

    本文主要内容是 CNN 的 BP 算法,看此文章前请保证对CNN有初步认识,可参考Neurons Networks convolutional neural network(cnn). 网络表示 CN ...

  4. Eclipse 打开编辑文件所在文件夹方法

    一个便捷的方法在eclipse的菜单中,依次点击Run->External Tools-> External Tools configurations添加一个新的工具 OpenContai ...

  5. String定义与方法

    //5种构造方法 public void Con(){ String str = "sfaj"; String str1 = new String("sfajdf&quo ...

  6. Linux makefile教程之书写命令四[转]

    书写命令———— 每 条规则中的命令和操作系统Shell的命令行是一致的.make会一按顺序一条一条的执行命令,每条命令的开头必须以[Tab]键开头,除非,命令是紧跟 在依赖规则后面的分号后的.在命令 ...

  7. 【c++】输出 0000,0001,0002,0003,0004...这样的字符串

    #include <iostream> #include <iomanip> ; ){ stringstream buf; buf <<setfill()<& ...

  8. SlidingPaneLayout的基本使用

      SlidingPaneLayout是V4包中新添加的组件,可以实现两列面板的切换.说先来看看API文档的说明: ? 1 SlidingPaneLayout provides a horizonta ...

  9. 机器学习(1)_R与神经网络之Neuralnet包

    本篇博客将会介绍R中的一个神经网络算法包:Neuralnet,通过模拟一组数据,展现其在R中是如何使用,以及如何训练和预测.在介绍Neuranet之前,我们先简单介绍一下神经网络算法. 人工神经网络( ...

  10. Hadoop2的简单安装

    前面花了很多时间来介绍hadoop1的安装,随着hadoop的发展,hadoop2的应用也越来越普及,hadoop2解决了hadoop1中的很多问题,比如单点故障,namenode容量小的问题. 我们 ...