[主席树]HDOJ2665 && POJ2104 && POJ2761

主席树真是神奇的物种！

Orz一篇资料

题意：给n、m

　　   下面有n个数 (编号1到n)

　　　有m个询问，询问的是上面的数的编号在[l,r]之间第k小的数

n、m的范围都是$10^5$

是主席树的入门题

借此来学习一下主席树

主席数利用函数式线段树来维护数列，一般用来解决区间第k大问题

空间时间的复杂度小于树套树(常数小)

划分树也可以解决区间第k大问题，但划分树不支持修改，主席树可以(用树状数组维护)

(这三道入门题都是无修改的)

我们先来YY一下这种求区间第k(大)小的题目···

最容易想到的做法就是对于每个询问，对[l, r]区间排个序，输出第k小

　　　　　这样的复杂度是O($m\times nlogn$)

大家都很容易想到排序，但是对于每个询问每个区间排序的代价太大了...

再想想，让我们加入一些线段树的思想，

要求第k小，也就是与个数相关，那么我们可以 以[l,r]区间内的数的个数来建立一棵线段树

结点的值是数的个数，当我们要找第k小的数时，若左子树大于k，那么很显然第k小的数在左子树中；若左子树小于k，那么第k小的数在右子树中

建树的复杂度是O(nlogN)，查询的复杂度是O(logN)      (这里的N是不相同数的数量)

若我们仍对每个查询建树，那么复杂度丝毫没有降低(反而提高了)，那有没有什么办法可以不要每次查询都建树呢？

(让我们联想一下前缀和) 假设我们知道[1, l-1]之间有多少个数比第k小的数小，那么我们只要减去这些数之后在[1, r]区间内第k小的数即是[l, r]区间内的第k小数

更确切的说，我们要求[l, r]区间内的第k小数  可以 用以[1, r]建立的线段树去减去以[1, l-1] 建立的线段树

这样能够减的条件是这两棵树必须是同构的。

若是不太明白， 我们来举个例子：

如有序列  1 2 5 1 3 2 2 5 1 2

我们要求 [5,10]第5小的数

(数列中不存在4、6、7、8 但根据原理就都写出来了，为方便理解，去掉了hash的步骤，实际的代码中其实只要一棵4个叶子节点的树即可)

(红色的为个数)

我们建立的[1, l-1] (也就是[1, 4])之间的树为

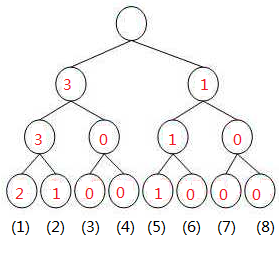
[1, r]也就是[1, 10]的树为

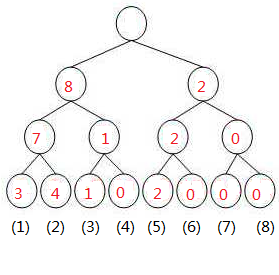
两树相减得到

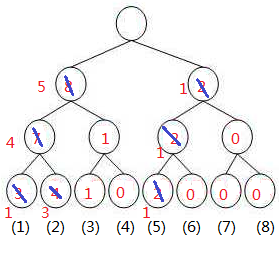
我们来找第5小的数：

发现左子树为5  所以第5小的数在左边， 再往下(左4右1) 发现左边小于5了 ，所以第5小的数在右边 所以第5小的数就是3了

同样的，我们只要建立[1, i] (i是1到n之间的所有值)的所有树，每当询问[l, r]的时候，只要用[1, r]的树减去[1, l-1]的树，再找第k小就好啦

我们将这n个树看成是建立在一个大的线段树里的，也就是这个线段树的每个节点都是一个线段树( ——这就是主席树)

最初所有的树都是空树，我们并不需要建立n个空树，只要建立一个空树，也就是不必每个节点都建立一个空树

插入元素时，我们不去修改任何的结点，而是返回一个新的树( ——这就是函数式线段树)

因为每个节点都不会被修改，所以可以不断的重复用，因此插入操作的复杂度为O(logn)

总的复杂度为O((n+m)lognlogN)   (听说 主席树的芭比说 加上垃圾回收， 可以减少一个log~~~ 然而这只是听说)

你以为这样就结束了吗！！

你没有发现这样空间大到爆炸吗！！！

你在每个节点都建了一个线！段！树！这不MLE才有鬼呢！！！

那怎么办呢？

$T_i$表示一棵[1, i]区间的线段树

那么$T_i$与$T_{i-1}$的区别就只有当前插入的这个元素$a_i$以及它的父亲以及他父亲的父亲以及他父亲的父亲的父亲...

也就是改变的就只有他和他上面logn个数

所以，我们并不需要建一整棵树，我们只需要 单独建立logn个结点，跟$T_{i-1}$连起来就好了

这样树的空间复杂度(NlogN)

以下是代码：

 #define lson l, m
 #define rson m+1, r
 const int N=1e5+;
 int L[N<<], R[N<<], sum[N<<];
 int tot;
 int a[N], T[N], Hash[N];
 int build(int l, int r)
 {
     int rt=(++tot);
     sum[rt]=;
     if(l<r)
     {
         int m=(l+r)>>;
         L[rt]=build(lson);
         R[rt]=build(rson);
     }
     return rt;
 }

 int update(int pre, int l, int r, int x)
 {
     int rt=(++tot);
     L[rt]=L[pre], R[rt]=R[pre], sum[rt]=sum[pre]+;
     if(l<r)
     {
         int m=(l+r)>>;
         if(x<=m)
             L[rt]=update(L[pre], lson, x);
         else
             R[rt]=update(R[pre], rson, x);
     }
     return rt;
 }

 int query(int u, int v, int l, int r, int k)
 {
     if(l>=r)
         return l;
     int m=(l+r)>>;
     int num=sum[L[v]]-sum[L[u]];
     if(num>=k)
         return query(L[u], L[v], lson, k);
     else
         return query(R[u], R[v], rson, k-num);
 }

 int main()
 {
 //    int t;
 //    scanf("%d", &t);
 //    while(t--)
 //    {
         tot=;
         int n, m;
         scanf("%d%d", &n, &m);
         for(int i=; i<=n; i++)
         {
             scanf("%d", &a[i]);
             Hash[i]=a[i];
         }
         sort(Hash+, Hash+n+);
         int d=unique(Hash+, Hash+n+)-Hash-;
         T[]=build(, d);
         for(int i=; i<=n; i++)
         {
             int x=lower_bound(Hash+, Hash+d+, a[i])-Hash;
             T[i]=update(T[i-], , d, x);
         }
         while(m--)
         {
             int l, r, k;
             scanf("%d%d%d", &l, &r, &k);
             int x=query(T[l-], T[r], , d, k);
             printf("%d\n", Hash[x]);
         }
 //    }
 }

POJ 2104 && HDOJ 2665 && POJ 2761

能修改的戳这里~~~~~