TYVJ P1075 硬币游戏 Label：dp

背景

农民John的牛喜欢玩硬币，所以John就为它们发明了一个新的两人硬币游戏，叫做Xoinc。

描述

最初地面上有一堆n个硬币(5<=n<=2000)，从上面数第i个硬币的价值为C_i(1<=C_i<=100000);

游戏开始后，A先取一枚或两枚硬币。如果A取了一枚，那么B可以继续取一枚或两枚；如果A取了两枚，那么B可以取一到四枚硬币。每次都只能从最上面取。每一次，当前取硬币的人都至少取一枚硬币，最多可以取他的对手上一次取硬币数目的两倍。当没有硬币可取的时候，游戏就结束了。

然后，他们就可以用得到的硬币向John买东西，当然，他们游戏的目的就是要尽可能使自己得到的硬币价值更大。现在你的任务是，求出在两个人都想得到更大价值的情况下，游戏结束后，第一个人最多能得到的硬币价值。

输入格式

第1行：一个整数，N（5<=N<=2000）。

第2到n+1行：第 i+1 行代表从上数第i枚硬币的价值。

输出格式

一行：一个数字，第一个人能得到的最大价值

测试样例1

输入

5
1
3
1
7
2

输出

9

备注

usaco nov09 Ag
translated by pricez

思路集合

解题思路

首先明确这是一题DP题目
那么不难发现几个必须枚举的状态
1、对方在上一轮取了几个（这个直接影响我方这回合取的数目）
2、当前还剩多少个可以取
3、我方这回合取了多少个
接着
假设上回合对方拿走了J个后还剩I个可供我们这回合拿取，那么可以推出我们能拿的硬币数的范围在1~2*J之间则可以列出
F[I,J]:=MAX（SUM[I]-F[I-K,K]）；（1<=K<=2*J）
其中SUM[I]表示剩下的I个硬币的总面值
K表示我当前这回合拿了多少个
因为双方都是最优的取法来取
所以F[I-K,K]表示的就是对手在我拿走K个硬币还剩下I-K个硬币的情况他最多能取的面值大小
因而SUM[I]-F[I-K,K]表示的意义就是我在剩下的硬币中能取得的最多的面值大小
初始状态是F[0,1~N]=0;
末状态是F[N,1]

理解了上面的方程后
可以看出方程的时间复杂度就是O(N^3)显然会超时
这时候就需要优化
我们观察
F[I,J]的方程与F[I,J-1]的方程
可以发现
F[I,J-1]所枚举的所有状态在F[I,J]时又枚举了一遍，明显这是多余的
可以看出F[I,J]比F[I,J-1]多枚举的只有SUM[I]-F[I-(2*J-1),2*J-1]和SUM[I]-F[I-2*J,2*J]两项
所以方程可以改写成
F[I,J]:=MAX(F[I,J-1],MAX(SUM[I]-F[I-(2*J-1),2*J-1],SUM[I]-F[I-2*J,2*J]));
这样就优化到O(N^2)了
基本调试清楚下就可以AC了
---------------------
其实不需如上优化
第一个方程+单调队列足以AC

转载：

http://www.cnblogs.com/iwtwiioi/p/3973258.html

我们发现，每一个阶段都由上一个玩家决定的，即别人怎么拿限制了我怎么拿，那么

设状态为f(i, j)表示剩余i个硬币，上次拿了j个硬币，注意，是上一次！

则

f(i, j)=max{sum(1, i)-f(i-k, k)} 1<=k<=2*j

这点可以参照前边一题的dp博弈

sum(1, i)包含了2重意思，即sum(1, i-k), sum(i-k+1, i)，前者是之前局面的和，后者是玩家所得的价值

而f(i-k, k)的意思就是根据上一次所拿硬币j限制了我这次拿硬币k，而这个状态就表示我这次拿了k个之后还剩与i-k个，而且是从我这个状态k个限制了它所拿硬币。

然后注意读入是倒序即可

但是这样做状态是n^2，转移n，显然2000的数据tle。

那么我们要优化

我们来看看f(10,1)的情况。

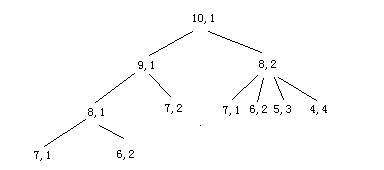
在这里，我们发现f(8,2)和f(8,1)的区别就是比其多了2条路，所以我们完全能想到以下方法。

将除了自己特有的两条路保留后，另两条路舍去，直接连到f(8,1)的最优解上，这样就能将时间复杂度优化为O(n^2)，这样的话，我们的状态转移方程可以写为f(x,y)=Max{ f(x,y-1),sum[x]-Min{f(x-(2*y-1),2*y-1),f(x-2*y,2*y)} }

附不懂的代码

#include<iostream>

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

int N,a[],f[][],sum[];

int main(){

//    freopen("01.txt","r",stdin);

    scanf("%d",&N);

    for(int i=N;i>;i--)

        scanf("%d",&a[i]);

    for(int i=;i<=N;i++)

        sum[i]=sum[i-]+a[i];

    for(int i=;i<=N;i++)

        for(int j=;j<=N;j++){

            f[i][j]=f[i][j-];//自己特有的两条路保留，直接连到f(i,j-1)的最优解上

            if(i-(j<<)>=)

                f[i][j]=max(f[i][j],sum[i]-f[i-(j<<)][j<<]);

            if(i-((j<<)-)>=)

                f[i][j]=max(f[i][j],sum[i]-f[i-((j<<)-)][(j<<)-]);

        }

    printf("%d\n",f[N][]);

    return ;

}