HDU 4576 DP

Robot

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 5363    Accepted Submission(s): 1584

Problem Description

Michael has a telecontrol robot. One day he put the robot on a loop with n cells. The cells are numbered from 1 to n clockwise.

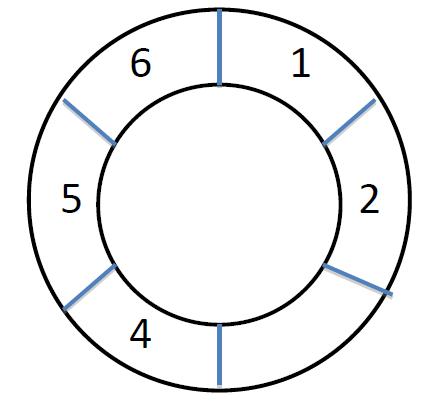
At first the robot is in cell 1. Then Michael uses a remote control to send m commands to the robot. A command will make the robot walk some distance. Unfortunately the direction part on the remote control is broken, so for every command the robot will chose a direction(clockwise or anticlockwise) randomly with equal possibility, and then walk w cells forward.
Michael wants to know the possibility of the robot stopping in the cell that cell number >= l and <= r after m commands.

 

Input

There are multiple test cases. 
Each test case contains several lines.
The first line contains four integers: above mentioned n(1≤n≤200) ,m(0≤m≤1,000,000),l,r(1≤l≤r≤n).
Then m lines follow, each representing a command. A command is a integer w(1≤w≤100) representing the cell length the robot will walk for this command.  
The input end with n=0,m=0,l=0,r=0. You should not process this test case.

 

Output

For each test case in the input, you should output a line with the expected possibility. Output should be round to 4 digits after decimal points.

 

Sample Input

3 1 1 2

1

5 2 4 4

1
2

0 0 0 0

 

Sample Output

0.5000

0.2500

 

Source

2013ACM-ICPC杭州赛区全国邀请赛

 

题意：

有长度为n的环，有m次操作，每次输入一个数w，可以选择顺时针或者逆时针走w步，问最后停在l区间[l,r]的概率。最初在1点。

输入n，m，l，r；

代码：

//这一步的状态只有上一步的状态决定，可列转移方程，但显然要用滚动数组优化。
//注意的是中间过程中有太多的取模运算，直接算会超时所以先预处理出来取模的值再算
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,l,r,mp[];
double dp[][];
int main()
{
    while(scanf("%d%d%d%d",&n,&m,&l,&r)==){
        if(n==&&m==&&l==&&r==) break;
        for(int i=;i<=;i++) mp[i]=i%n;
        int x;
        l--;r--;
        memset(dp,,sizeof(dp));
        dp[][]=;
        for(int i=;i<=m;i++){
            int I=i&;
            scanf("%d",&x);
            x%=n;
            for(int j=;j<n;j++){
                int tmp=mp[j+x];
                dp[I][tmp]+=dp[!I][j]*0.5;
                tmp=mp[j+(n-x)];
                dp[I][tmp]+=dp[!I][j]*0.5;
            }
            memset(dp[!I],,sizeof(dp[!I]));
        }
        double sum=;
        int I=m&;
        for(int i=l;i<=r;i++)
            sum+=dp[I][i];
        printf("%.4lf\n",sum);
    }
    return ;
}