《剑指offer》---跳台阶问题

本文算法使用python3实现

---

1. 问题1

1.1 题目描述：

  一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

  时间限制：1s；空间限制：32768K

---

1.2 思路描述：

  （1）当 $ n=0 $ 时，返回0

  （2）当 $ n=1 $ 时，只有一种跳法：跳1级台阶。

  （3）当 $ n=2 $ 时，有两种跳法：(a) 跳1级再跳1级；(b) 直接跳2级。

  （4）当 $ n=3 $ 时，我们只考虑最后一步的情况：(a)当最后一步只跳1级时， $ f(3)=f(3-1) $ ；(b)当最后一步直接跳2级时， $ f(3)=f(3-2) $ 。因此 $ f(3)=f(3-1) + f(3-2) $

  （5）以此类推，当 $ n=N $ 时，只需考虑最后一步的情况即可：(a)当最后一步只跳1级时， $ f(N)=f(N-1) $ ；(b)当最后一步直接跳2级时， $ f(N)=f(N-2) $ 。因此 $ f(N)=f(N-1) + f(N-2) $

---

1.3 程序代码：

class Solution:
    # def jumpFloor(self, number):
    #     '''递归:提交代码超时了'''
    #     if number in [0, 1, 2]:
    #     	return number
    #     return self.jumpFloor(number-1)+self.jumpFloor(number-2)

    def jumpFloor(self, number):
        '''迭代'''
        floor = []
        for i in range(number+1):
        	if i in [0,1,2]:
        		floor.append(i)
        		continue
        	floor.append(floor[i-1]+floor[i-2])
        return floor[-1]

---

2. 问题2

2.1 题目描述：

  一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法

  时间限制：1s；空间限制：32768K

---

2.2 思路描述：

  （1）当 $ n=0 $ 时，返回0

  （2）当 $ n=1 $ 时，只有一种跳法：跳1级台阶。

  （3）当 $ n=2 $ 时，有两种跳法：(a) 跳1级再跳1级；(b) 直接跳2级。

  （4）当 $ n=3 $ 时，我们只考虑最后一步的情况：(a)当最后一步只跳1级时， $ f(3)=f(3-1) $ ；(b)当最后一步直接跳2级时， $ f(3)=f(3-2) $ ；(c) 当最后一步直接跳3级时， $ f(3) = 1 $ 。因此 $ f(3)=f(3-1) + f(3-2) +1 $

  （5）以此类推，当 $ n=N $ 时，只需考虑最后一步的情况即可：(a)当最后一步只跳1级时， $ f(N)=f(N-1) $ ；(b)当最后一步直接跳2级时， $ f(N)=f(N-2) $ ；(c) 当最后一步直接跳3级时， $ f(N) = f(N-3) $；...；(n)当最后一步直接跳N级时， $ f(N) = 1 $ 。因此 $ f(N) = f(N-1)+f(N-2)+f(N-3)+...+f(1)+1 $

---

2.3 程序代码：

class Solution:
    def jumpFloorII(self, number):
        '''迭代法，保存n次结果'''
        floor = []
        for i in range(number+1):
        	if i in [0,1,2]:
        		floor.append(i)
        		continue
        	step = 0
        	for k in range(i):
        		step += floor[k]
        	floor.append(step+1)
        return floor[-1]

    # def jumpFloorII(self, number):
    #     '''递归法：当number很大时，递归很深，会超时'''
    #     if number in [0,1,2]:
    #     	return number
    #     res = 0
    #     for k in range(number):
    #     	res += self.jumpFloorII(k)
    #     return res+1

---

3. 问题3

3.1 题目描述：

  我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

  时间限制：1s；空间限制：32768K

---

3.2 思路描述：

  （1）当 $ n=0 $ 时，返回0

  （2）当 $ n=1 $ 时，只有一种覆盖方法，即竖着覆盖。

    

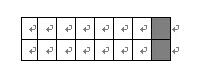
  （3）当 $ n=2 $ 时，有两种覆盖方法：使用两个 $ 2\times1 $ 的小矩形，横着覆盖与竖着覆盖。

    

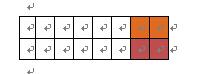
  （4）当 $ n=3 $ 时，我们只考虑最后一步的情况：(a)当最后一步只需覆盖一个 $ 2\times1 $ 的矩形时时， $ f(3)=f(3-1) $ ；(b)当最后一步需覆盖一个 $ 2\times2 $ 的矩形时， $ f(3)=f(3-2) $

  （5）以此类推，当 $ n=N $ 时，只需考虑最后一步的情况即可：(a)当最后一步只需覆盖一个 $ 2\times1 $ 的矩形时， $ f(N)=f(N-1) $ ；(b)当最后一步需覆盖一个 $ 2\times2 $ 的矩形时， $ f(N)=f(N-2) $ ；

---

3.3 程序代码：

class Solution:
	def rectCover(self, number):
		# 使用迭代法进行
		if number == 0:
			return 0
		methods = []
		for i in range(1,number+1):
			if i in [1,2]:
				methods.append(i)
			else:
				methods.append(methods[-1]+methods[-2])
		return methods[-1]