最近公共祖先LCA（前置知识）

1.前言

　　最近公共祖先（Least Common Ancestors），简称LCA，是由Tarjan教授（对，又是他）提出的一种在有根树中，找出某两个结点u和v最近的公共祖先问题。

2.什么是最近公共祖先？

　　在一棵树中，每个结点都有他的父亲和祖先，而最近公共祖先就是两个节点在这棵树上深度最大的公共的祖先节点。

　　换句话说，就是两个点在这棵树上距离最近的公共祖先节点。结合下图和文字应该很好的诠释了最近公共祖先：

　　PS:在LCA中，也可以将结点本身视为自己的祖先

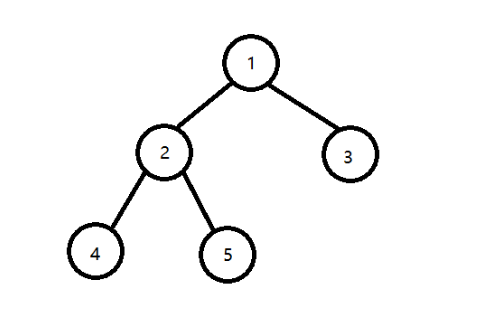
　　在这颗以结点1为根的树中，4与5的最近公共祖先是2，4和3的最近公共祖先是1，4和2的最近公共祖先是1，4和1的最近公共祖先是1。

3.什么是离线/在线算法

　　对于LCA问题，常见的方法有Tarjan（DFS+并查集），倍增，树链剖分，ST（DFS+ST表），后三个都是在线算法，而前一个则是离线算法（后续的LCA算法会按现在给出的顺序更新）。

　　那么什么是在/离线算法？这里引用一段百度百科的说法：

　　在线算法：“在线算法是指它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入。”

　　离线算法：“是指基于在执行算法前输入数据已知的基本假设，也就是说，对于一个离线算法，在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。”

　　这里举个例子，在线算法就是我们常说的“输入一组数据，输出一组数据”，而离线算法就是“输入完所有数据在输出答案”。　　

4.LCA问题的方法介绍：

1.Tarjan：戳我

2.倍增：戳我

3.树链剖分：没什么好讲的，把重链剖分看懂就差不多会了

4.ST表+DFS：