loj #6138. 「2017 山东三轮集训 Day4」Right

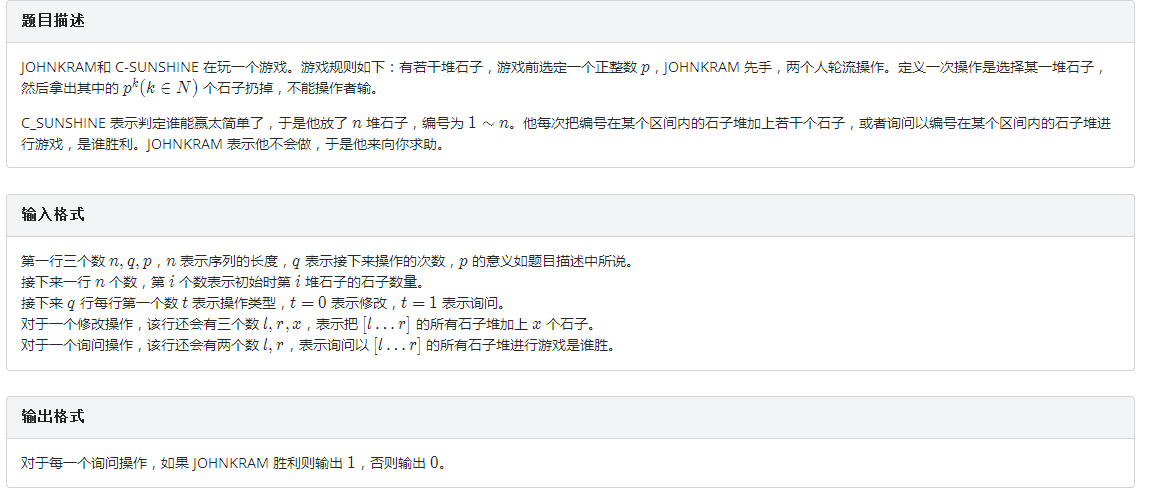
题目:

题解:

暴力一波 \(SG\) 函数可以发现这么一个规律:

• \(p\) 为奇数的时候 : \(SG(n) = n \% 2\)
• \(p\) 为偶数的时候 : \(SG(n) = n \% (p+1) == p ? 2 : n \% (p+1) \% 2\)

对于奇数的情况我们就可以直接用一棵支持区间取反和区间查询 \(1\) 的个数的线段树搞定。

那么难点在于偶数的情况。

我们可以采用分块算法.

每个块分别中保存 \(\bmod (p+1)\) 为奇数的数和为偶数的数。

然后每次查询的时候我们可以通过几次 \(lower_bound\) 来解决。

复杂度 \(O(m\log n)\space or\space O(m\sqrt{n}\log n)\)

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int*,int*> pa;
inline void read(int &x){
	x=0;static char ch;static bool flag;flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
const int maxn = 100010;
int n,q,p;
namespace work1{
	int T[maxn<<2],tag[maxn<<2],a[maxn];
	inline void push_down(int rt,int l,int r){
		if(l == r || tag[rt] == 0) return ;
		int mid = l+r >> 1;
		tag[rt<<1] ^= 1;
		if((mid-l+1)&1) T[rt<<1] ^= 1;
		tag[rt<<1|1] ^= 1;
		if((r-mid)&1) T[rt<<1|1] ^= 1;
		tag[rt] = 0;
	}
	void build(int rt,int l,int r){
		if(l == r){
			T[rt] = a[l]&1;
			return ;
		}int mid = l+r >> 1;
		build(rt<<1,l,mid);build(rt<<1|1,mid+1,r);
		T[rt] = T[rt<<1]+T[rt<<1|1] & 1;
	}
	int L,R;
	void modify(int rt,int l,int r){
		if(L <= l && r <= R){
		    tag[rt] ^= 1;
			if((r-l+1)&1) T[rt] ^= 1;
			return ;
		}int mid = l+r >> 1;push_down(rt,l,r);
		if(L <= mid) modify(rt<<1,l,mid);
		if(R >  mid) modify(rt<<1|1,mid+1,r);
		T[rt] = T[rt<<1]+T[rt<<1|1] & 1;
	}
	int query(int rt,int l,int r){
		if(L <= l && r <= R) return T[rt];
		int mid = l+r >> 1;push_down(rt,l,r);
		if(R <= mid) return query(rt<<1,l,mid);
		if(L >  mid) return query(rt<<1|1,mid+1,r);
		return query(rt<<1,l,mid) + query(rt<<1|1,mid+1,r) & 1;
	}
	int main(){
		rep(i,1,n) read(a[i]);
		build(1,1,n);
		int op,x;
		while(q--){
			read(op);
			if(op == 0){
				read(L);read(R);read(x);
				if(x & 1) modify(1,1,n);
			}else{
				read(L);read(R);
				printf("%d\n",query(1,1,n));
			}
		}
		return 0;
	}
}
namespace work2{
	const int maxm = 322;
	int tmp[maxn],c[maxn];
	struct Node{
		int a[maxm],b[maxm],tag;
		int cnta,cntb,l,r;
		// a[i] % (p+1) = 1;
		// b[i] % (p+1) = 0;
		void build(int n){
			sort(tmp+1,tmp+n+1);
			cnta = cntb = 0;
			rep(i,1,n){
				if(tmp[i] % (p+1) & 1) a[++cnta] = tmp[i];
				else b[++cntb] = tmp[i];
			}return ;
		}
		int query_all(int &one,int &two){
			int x = (p - tag + (p+1)) % (p+1);pa pos;
			if(x & 1) pos = equal_range(a+1,a+cnta+1,x);
			else pos = equal_range(b+1,b+cntb+1,x);
			two += (pos.second - pos.first);
			if(tag <= (p-1)){
				x = p - 1 - tag;int ps = 0;
				if(x & 1) ps = upper_bound(a+1,a+cnta+1,x) - a - 1;
				else ps = upper_bound(b+1,b+cntb+1,x) - b - 1;
				one += ps;
			}
			if(tag >= 2){
				x = p - tag;int ps = 0;
				if(x & 1) ps = cnta - (upper_bound(a+1,a+cnta+1,x)-a-1);
				else ps = cntb - (upper_bound(b+1,b+cntb+1,x)-b-1);
				one += ps;
			}
		}
		void query(int l,int r,int &one,int &two){
			int cnt = 0;
			rep(i,this->l,this->r){
				c[i] += tag;
				if(c[i] >= p+1) c[i] -= p+1;
				tmp[++cnt] = c[i];
			}sort(tmp+1,tmp+cnt+1);
			cnta = cntb = tag = 0;
			rep(i,1,cnt){
				if(tmp[i] % (p+1) & 1) a[++cnta] = tmp[i];
				else b[++cntb] = tmp[i];
			}
			rep(i,l,r){
				if(c[i] % (p+1) == p) ++ two;
				else if(c[i] % (p+1) & 1) ++ one;
			}return ;
		}
		void modify(int l,int r,int x){
			int cnt = 0;
			rep(i,this->l,this->r){
				c[i] += tag;if(c[i] >= (p+1)) c[i] -= (p+1);
				if(l <= i && i <= r){
					c[i] += x;
					if(c[i] >= (p+1)) c[i] -= (p+1);
				}
				tmp[++cnt] = c[i];
			}sort(tmp+1,tmp+cnt+1);
			cnta = cntb = tag = 0;
			rep(i,1,cnt){
				if(tmp[i] % (p+1) & 1) a[++cnta] = tmp[i];
				else b[++cntb] = tmp[i];
			}return ;
		}
	}zs[maxm];
	int belong[maxn];
	inline void modify(int l,int r,int x){
		if(belong[l] == belong[r]) return zs[belong[l]].modify(l,r,x);
		zs[belong[l]].modify(l,zs[belong[l]].r,x);
		zs[belong[r]].modify(zs[belong[r]].l,r,x);
		rep(i,belong[l]+1,belong[r]-1){
			zs[i].tag += x;
			if(zs[i].tag >= (p+1)) zs[i].tag -= (p+1);
		}
		return ;
	}
	inline int query(int l,int r){
		int res1 = 0,res2 = 0;
		if(belong[l] == belong[r]){
			zs[belong[l]].query(l,r,res1,res2);
		}else{
			zs[belong[l]].query(l,zs[belong[l]].r,res1,res2);
			zs[belong[r]].query(zs[belong[r]].l,r,res1,res2);
			rep(i,belong[l]+1,belong[r]-1) zs[i].query_all(res1,res2);
		}
		if((res1 & 1) || (res2 & 1)) return 1;
		else return 0;
	}
	int main(){
		int block = ceil(sqrt(n));
		int sz = 0,m = 1;
		zs[1].l = 1;
		rep(i,1,n){
			belong[i] = m;read(tmp[++sz]);
			c[i] = (tmp[sz] %= (p+1));
			if(sz == block){
				zs[m].build(sz);
				zs[m].r = i,zs[++m].l = i+1;
				sz = 0;
			}
		}
		if(zs[m].l != n+1){
			zs[m].r = n;
			zs[m].build(n-zs[m].l+1);
		}else --m;
		int op,l,r,x;
		while(q--){
			read(op);read(l);read(r);
			if(op == 0) read(x),modify(l,r,x % (p+1));
			else printf("%d\n",query(l,r));
		}
		return 0;
	}
}
int main(){
	read(n);read(q);read(p);
	if(p & 1) work1::main();
	else work2::main();
	return 0;
}