Dijkstra算法构造单源点最短路径

迪杰斯特拉(Dijkstra)算法

是求从某个源点到其余各顶点的最短路径，即对已知图 G=（V，E），给定源顶点 s∈V，找出 s 到图中其它各顶点的最短路径。

我总结下核心算法，伪代码如下：

Dijkstra()
{
    初始化Dist、Path、final

    // 每次求得v0到某顶点v的最短路径
    while (图的顶点数-)
    {
        . 找到非最短路径顶点集中距V0最近的顶点v 得到其顶点下标和距离
           将v加入到最短距离顶点集合中
           打印相关内容

        . 依次修改其它未得到最短路径顶点的Dist[k]值
           假设求得最短路径的顶点为u，
           则 Dist[k] ＝min( Dist[k], Dist[u] + G.arcs[u][k] )
           同时修改Path[k]:Path[k] = Path[u] +G.vex[k]
    }
}

实例：

源代码：

 #include <iostream>
 #include <stdio.h>
 #include <stdlib.h>
 #include <string>
 using namespace std;

 #define MAX_VERTEX_NUM 100
 #define MAX_EDGE_NUM 200
 #define MAX_VERTEX_NAMELEN 100
 #define INF 65535

 typedef struct{
     char name[MAX_VERTEX_NAMELEN];
 }VerType;

 // 图的邻接矩阵存储结构
 typedef struct{
     int VertexNum,EdgeNum;                        // 顶点数，边数
     VerType Vertex[MAX_VERTEX_NUM];               // 顶点集
     int Edge[MAX_VERTEX_NUM][MAX_VERTEX_NUM];     // 边集
 }MGragh;

 // 邻接矩阵建图
 void CreateMGragh(MGragh *Gra)
 {
     int i,j,k,w;
     char v1[MAX_VERTEX_NAMELEN],v2[MAX_VERTEX_NAMELEN];

     printf("请输入顶点数及边数(顶点数 边数)\n");
     scanf("%d %d%*c",&(Gra->VertexNum),&(Gra->EdgeNum));

     printf("请输入顶点信息\n");
     for (i=; i<Gra->VertexNum; i++){
         printf("%d.",i+);
         gets(Gra->Vertex[i].name);
     }

     // 初始化邻接矩阵
     for (i=; i<Gra->VertexNum; i++){
         for (j=; j<Gra->VertexNum; j++){
             if (i==j){
                 Gra->Edge[i][j] = ;        // 各点到自己的距离为0
             }
             else{
                 Gra->Edge[i][j] = INF;        // 各点到不相邻的点距离为无穷
             }
         }
     }

     printf("请输入边信息(顶点，顶点，权值)\n");
     for (i=; i<Gra->EdgeNum; i++){
         printf("%d.",i+);
         scanf("%[^,]%*c%[^,]%*c%d%*c",v1,v2,&w);

         for (j=; j<Gra->VertexNum; j++){
             for (k=; k<Gra->VertexNum; k++){
                 if (strcmp(Gra->Vertex[j].name,v1) ==  && strcmp(Gra->Vertex[k].name,v2) == ){
                     Gra->Edge[j][k] = w;
                 }
             }
         }
     }
 }

 int Dist[MAX_VERTEX_NUM];            // 存储VO到各点的最短路径的权值和
 string ShortPath[MAX_VERTEX_NUM];    // 存储V0到各点的最短路径

 void ShortPathByDijkstra(MGragh *Gra,int vo)
 {
     printf("\n最短路径为:\n");
     int v,w,k,min;
     int final[MAX_VERTEX_NUM];    // final[w]=1 表示已经求得顶点V0到Vw的最短路径

     // 初始化数据
     for (v=; v<Gra->VertexNum; v++){
         final[v] = ;                    // 全部顶点初始化为未找到最短路径
         Dist[v] = Gra->Edge[vo][v];        // 将与vo点有连线的顶点加上权值
         if (Dist[v] != INF && Dist[v] != ){
             ShortPath[v] += Gra->Vertex[vo].name;
             ShortPath[v] += Gra->Vertex[v].name;
         }
         else{
             ShortPath[v] = "";
         }    // 记录由V0连出去的边的路径 如AB、AC
     }
     Dist[vo] = ;        // v0到自己的路径为0
     final[vo] = ;        // 标记已经找到v0到自己的最短路径

     // 每次求得vo到某顶点V的最短路径
     for (v=; v<Gra->VertexNum; v++){
         min = INF;

         // 将某点加入最短路径顶点集
         for (w=; w<Gra->VertexNum; w++){
             if (final[w] ==  && Dist[w]<min){
                 k = w;
                 min = Dist[w];
             }
         }    // 找到非最短路径顶点集中距V0最近的顶点 得到其顶点下标和距离
         final[k] = ;    // 将目前找到最近的顶点置1 即将该点加入最短路径顶点集
         printf("%d\t",Dist[k]);
         cout << ShortPath[k] << endl;

         // 修正当前最短路径及距离
         for (w=; w<Gra->VertexNum; w++){
             // 如果经过v顶点的路径比现在这条路径的长度短的话就更新
             if (final[w] ==  && (min+Gra->Edge[k][w]) < Dist[w]){
                 Dist[w] = min + Gra->Edge[k][w];
                 ShortPath[w] = ShortPath[k];
                 ShortPath[w] += Gra->Vertex[w].name;
             }
         }
     }
 }

 int main()
 {
     MGragh g;
     CreateMGragh(&g);
     ShortPathByDijkstra(&g,);
     return ;
 }

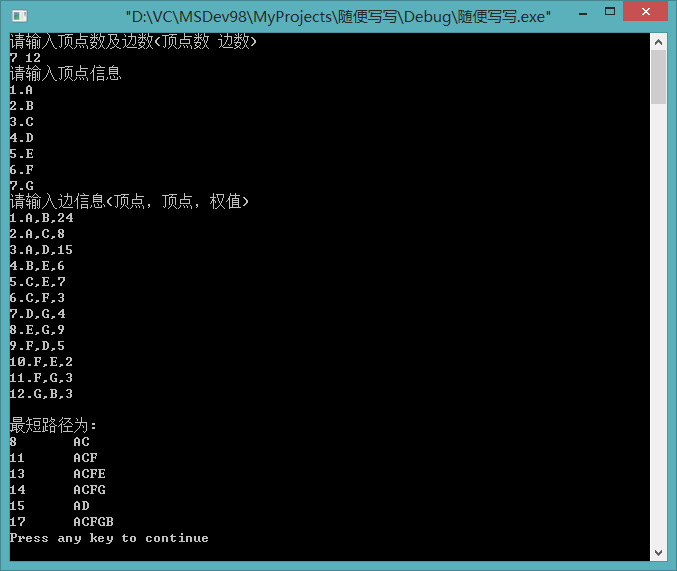
测试用例及结果：