2020-11-24：n个物品每个物品都有一定价值，分给2个人，怎么分两个人的价值差最小？

福哥答案2020-11-24：

背包问题：背包容量是SUM/2. 每个物体的体积是数的大小，然后尽可能的装满背包。

golang代码如下：

package main

import (
    "fmt"
)

//https://blog.csdn.net/qq_26222859/article/details/69335310?utm_source=blogxgwz4    ;背包问题变种：将数组分成两部分使得两部分的和的差最小
func main() {
    //vec := []int{1, 2, 3, 4, 5}

    //vec := []int{1, 5, 1, 1}

    //vec := []int{5, 2, 1}

    vec := []int{1, 0, 1, 7, 2, 4}

    //vec := []int{10, 7, 6, 5, 4}

    //vec := []int{1, 1, 2, 4, 5, 5, 6} //1,1,5,5    2,4,6    另一个：1 2 4 5和1,5,6
    //vec := []int{1, 1, 2, 4, 4}
    fmt.Println("最小差：", diff(vec))
    //fmt.Println(Knapsack01(vec, vec, 4))
}

func diff(arr []int) int {
    sum := 0
    arrLen := len(arr)
    for i := 0; i < arrLen; i++ {
        sum += arr[i]
    }
    halfOfSum := sum / 2
    // 确定矩阵二维定义：第一维代表前i个物体，i可为0；第二维代表从0开始的连续容量值
    // 确定矩阵长宽，并初始化。因为矩阵第一维和第二维都是从0开始，所以要加一
    matrix_firstDimensionLen := arrLen + 1
    matrix_secondDimensionLen := halfOfSum + 1
    matrix := make([][]int, matrix_firstDimensionLen)
    for i := 0; i < matrix_firstDimensionLen; i++ {
        matrix[i] = make([]int, matrix_secondDimensionLen)
    }

    ////初始化矩阵边界为0
    //for i := 0; i < len(matrix[0]); i++ {
    //  matrix[0][i] = 0
    //}
    //for i := 0; i < len(matrix); i++ {
    //  matrix[i][0] = 0
    //}

    //arr的下标，是否与matrix的下标冲突:是的
    //matrix[i][j]定义：用前i个物体装容量为j的背包能够装下的最大值
    //arr[i]定义：第i+1个物体的大小，所以arr[i-1]才是第i个物体的大小
    //遍历从矩阵边界开始（不包括边界），所以i = 1， j = 1
    for i := 1; i < matrix_firstDimensionLen; i++ {
        for j := 1; j < matrix_secondDimensionLen; j++ {
            //如果第i件物体不装进背包
            matrix[i][j] = matrix[i-1][j]
            //如果第i件物体装进背包     //备注：j - arr[i-1] >= 0防止下标为负
            if j-arr[i-1] >= 0 && matrix[i-1][j-arr[i-1]]+arr[i-1] > matrix[i][j] {
                matrix[i][j] = matrix[i-1][j-arr[i-1]] + arr[i-1]
                //fmt.Println(matrix[i][j], "i=", i, ",j=", j, "i-1=", i-1, ",j-arr[i-1]=", j-arr[i-1], ",左=", matrix[i-1][j-arr[i-1]], ",右=", arr[i-1])
            }
        }
        //fmt.Println("-----")
    }
    for i := 0; i < len(matrix); i++ {
        for j := 0; j < len(matrix[i]); j++ {
            fmt.Printf("%d\t", matrix[i][j])

        }
        fmt.Println("")
    }
    //System.out.println(matrix[len][halfOfSum]);
    fmt.Println(matrix[arrLen][halfOfSum])
    return sum - matrix[arrLen][halfOfSum]*2
}

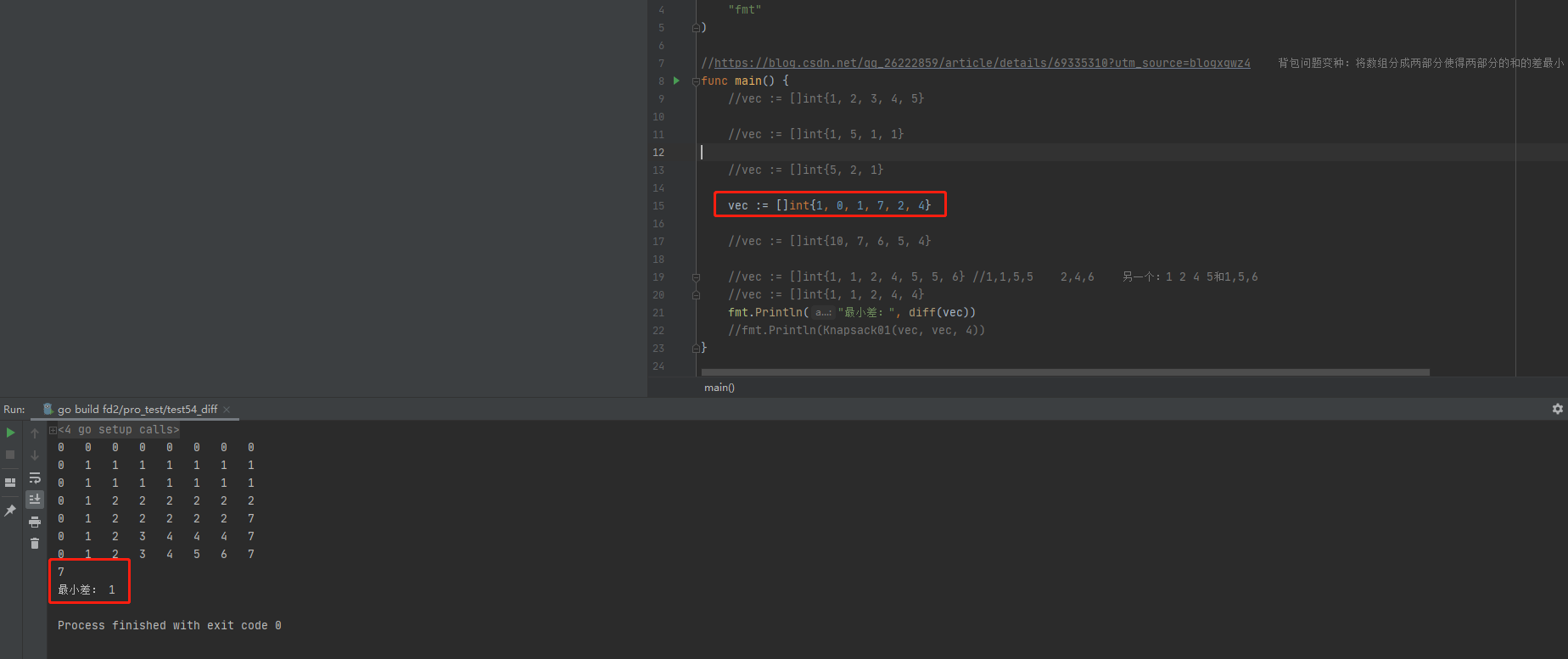
　　执行结果如下：