棋盘覆盖(java实现)
棋盘覆盖
问题描述
在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
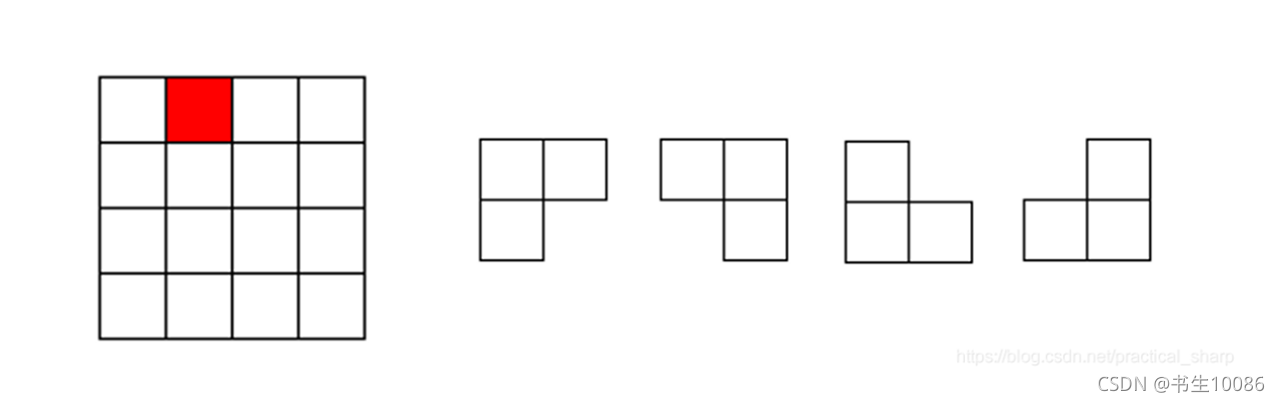
2.思路

1.当k>0时,将2k*2k棋盘分割为4个2(k-1)*2(k-1)子棋盘
2.将这三个无特殊方格的子棋盘转换为特殊棋盘,用一个L型骨盘覆盖这三个较小棋盘的会和处
3.递归地使用这种分割方法,直至棋盘简化为1*1棋盘,就结束递归。
3.注意
1.每次都对分割后的四个小棋盘进行判断,判断特殊方格是否在里面。
这里的判断的方法是每次先记录下整个大棋盘的左上角方格的行列坐标,然后再与特殊方格坐标进行比较,就可以知道特殊方格是否在该块棋盘中。
- 如果特殊方块在里面,这直接递归下去求即可,
- 如果不在,这根据分割的四个棋盘的不同位置,把右下角、左下角、右上角或者左上角的方格标记为特殊方块,然后继续递归。在递归函数里,还要有一个变量s来记录边的方格数,每次对棋盘进行划分时,边的方格数都会减半,这个变量是为了方便判断特殊方格的位置。
左上角方格的行列坐标是确定的,根据棋盘的大小和要判断在哪个区域确定
实现细节:
用4*4的棋盘举例
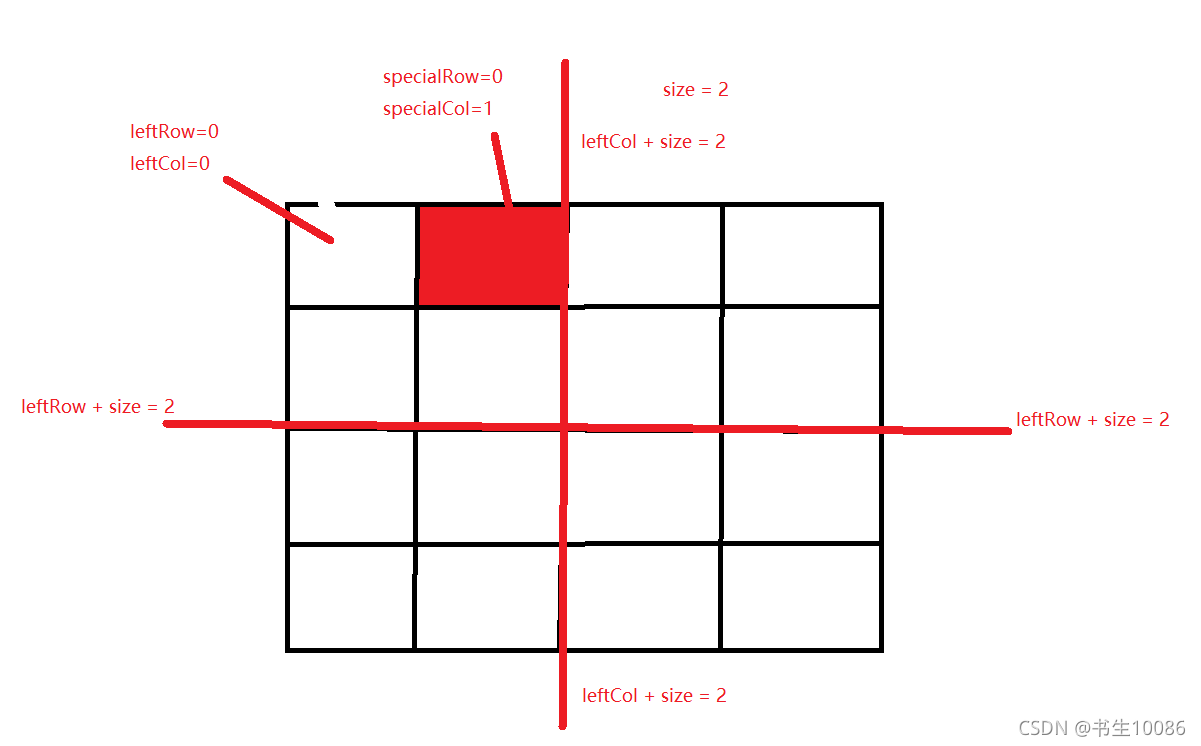
要判断特殊的方格在哪一个区域:
根据传入的参数size,leftRow,leftCol可以将棋盘划分为四个区域,然后和特殊点比较
1. 左上角:`specialRow < leftRow+size && specialCol < leftCol+size`
2. 右上角:`specialRow < leftRow+size && specialCol >= leftCol+size`
3. 左下角:`specialRow >= leftRow+size && specialCol < leftCol+size`
4. 右下角:`specialRow >= leftRow+size && specialCol >= leftCol+size`
填充的特殊点也可以用这几个参数来确定
如果特殊点不在左上角,填充的特殊点在该区域的右下角leftRow+size-1,leftRol+size-1
如果特殊点不在右上角,填充的特殊点在该区域的左下角leftRow+size-1,leftRol+size
如果特殊点不在左下角,填充的特殊点在该区域的右上角leftRow+size,leftCol+size-1
如果特殊点不在右下角,填充的特殊点在该区域的左下角leftRow+size,leftCol+size
2.递归的结束条件
- size为1时
//大小为1时,结束递归
if (1 == size) {
return;
}
- size为2时
//大小为2时,结束递归
if(size == 2){
number++;
if(specialCol != leftCol || specialRow != leftRow)
board[leftRow][leftCol] = number;
if(specialCol != leftCol+1 || specialRow != leftRow+1)
board[leftRow+1][leftCol+1] = number;
if(specialCol != leftCol+1 || specialRow != leftRow)
board[leftRow][leftCol+1] = number;
if(specialCol != leftCol || specialRow != leftRow+1)
board[leftRow+1][leftCol] = number;
return;
}
4.代码
package com.java.test;
public class ChessProblem {
int size;//容量
int[][] board;//棋盘
int specialRow;//特殊点横坐标
static int number = 0;//L形编号,这个一定要是静态的,可以在任何地方访问到
int specialCol;//特殊点纵坐标
public ChessProblem(int specialRow, int specialCol, int size) {
this.size = size;
this.specialCol = specialCol;
this.specialRow = specialRow;
board = new int[size][size];
}
//specialRow 特殊点的行下标
//specialCol 特殊点的列下标
//leftRow 矩阵的左边起点行下标
//leftCol 矩阵左边起点的列下标
//size 棋盘的宽或者高
public void setBoard(int specialRow, int specialCol, int leftRow, int leftCol, int size) {
//大小为1时,结束递归
if (1 == size) {
return;
}
int subSize = size / 2;
number++;
int n = number;//注意这里一定要吧number存在当前的递归层次里,否则进入下一层递归全局变量会发生改变
//假设特殊点在左上角区域
if (specialRow < leftRow + subSize && specialCol < leftCol + subSize) {
setBoard(specialRow, specialCol, leftRow, leftCol, subSize);
}
else {
//不在左上角,设左上角矩阵的右下角就是特殊点(和别的一起放置L形)
board[leftRow + subSize - 1][leftCol + subSize - 1] = n;
setBoard(leftRow + subSize - 1, leftCol + subSize - 1, leftRow, leftCol, subSize);
}
//假设特殊点在右上方
if (specialRow < leftRow + subSize && specialCol >= leftCol + subSize) {
setBoard(specialRow, specialCol, leftRow, leftCol + subSize, subSize);
}
else {
//不在右上方,设右上方矩阵的左下角就是特殊点(和别的一起放置L形)
board[leftRow + subSize -1][leftCol + subSize] = n;
setBoard(leftRow + subSize -1, leftCol + subSize, leftRow, leftCol + subSize, subSize);
}
//特殊点在左下方
if (specialRow >= leftRow + subSize && specialCol < leftCol + subSize) {
setBoard(specialRow, specialCol, leftRow + subSize, leftCol, subSize);
}
else {
//不在左下方,设左下方矩阵的右上角就是特殊点(和别的一起放置L形)
board[leftRow + subSize][leftCol + subSize - 1] = n;
setBoard(leftRow + subSize, leftCol + subSize - 1, leftRow + subSize, leftCol, subSize);
}
//特殊点在右下角
if (specialRow >= leftRow + subSize && specialCol >= leftCol + subSize) {
setBoard(specialRow, specialCol, leftRow + subSize, leftCol + subSize, subSize);
}
else {
//不在右下角,设右下角矩阵的左上就是特殊点(和别的一起放置L形)
board[leftRow + subSize][leftCol + subSize] = n;
setBoard(leftRow + subSize, leftCol + subSize, leftRow + subSize, leftCol + subSize, subSize);
}
}
//输出棋盘
public void printBoard(int specialRow,int specialCol,int size) {
setBoard(specialRow, specialCol, 0, 0, size);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board.length; j++) {
System.out.print(board[i][j] + "\t");
}
System.out.println();
}
}
public static void main(String[] args) {
//棋盘的大小
int N = 8;
//特殊点的坐标
int specialRow = 0;
int specialCol = 1;
ChessProblem chessProblem = new ChessProblem(specialRow , specialCol , N);
chessProblem.printBoard(specialRow, specialCol, N);
}
}
5.运行截图
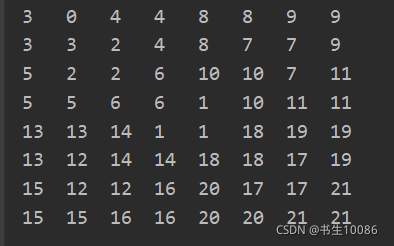
棋盘覆盖(java实现)的更多相关文章
- 递归与分治策略之棋盘覆盖Java实现
递归与分治策略之棋盘覆盖 一.问题描述 二.过程详解 1.棋盘如下图,其中有一特殊方格:16*16 . 2.第一个分割结果:8*8 3.第二次分割结果:4*4 4.第三次分割结果:2*2 5.第四次分 ...
- 棋盘覆盖(大数阶乘,大数相除 + java)
棋盘覆盖 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 在一个2k×2k(1<=k<=100)的棋盘中恰有一方格被覆盖,如图1(k=2时),现用一缺角的 ...
- 棋盘覆盖问题(算法分析)(Java版)
1.问题描述: 在一个2k×2k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有种情形.因而对任何 k≥0,有4k种不 ...
- NYOJ 45 棋盘覆盖
棋盘覆盖 水题,题不难,找公式难 import java.math.BigInteger; import java.util.Scanner; public class Main { public s ...
- bzoj 2706: [SDOI2012]棋盘覆盖 Dancing Link
2706: [SDOI2012]棋盘覆盖 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 255 Solved: 77[Submit][Status] ...
- NYOJ 45 棋盘覆盖 模拟+高精度
题意就不说了,中文题... 小白上讲了棋盘覆盖,于是我就挖了这题来做. 棋盘覆盖的推导不是很难理解,就是分治的思想,具体可以去谷歌下. 公式就是f(k) = f(k - 1) * 4 + 1,再化解下 ...
- 棋盘覆盖(一) ACM
棋盘覆盖 描述 在一个2k×2k(1<=k<=100)的棋盘中恰有一方格被覆盖,如图1(k=2时),现用一缺角的2×2方格(图2为其中缺右下角的一个),去覆盖2k×2k未被覆盖过的方格,求 ...
- CODEVS 2171 棋盘覆盖
2171 棋盘覆盖 给出一张nn(n<=100)的国际象棋棋盘,其中被删除了一些点,问可以使用多少12的多米诺骨牌进行掩盖. 错误日志: 直接在模板上调整 \(maxn\) 时没有在相应邻接表数 ...
- JavaScript编写棋盘覆盖
一.前言 之前做了一个算法作业,叫做棋盘覆盖,本来需要用c语言来编写的,但是因为我的c语言是半桶水(哈哈),所以索性就把网上的c语言写法改成JavaScript写法,并且把它的覆盖效果显示出来 二.关 ...
- TYVJ 1035 / codevs 2171 棋盘覆盖
Problem Description 给定一个n * m的棋盘,已知某些各自禁止放置,求最多往棋盘上放多少长度为2宽度为1的骨牌(骨牌不重叠) Input 第一行为n,m(表示有m个删除的格子)第二 ...
随机推荐
- Spark 读取HDFS csv文件并写入hive
package com.grady import org.apache.spark.SparkConf import org.apache.spark.sql.{Row, SaveMode, Spar ...
- docker-compose部署elastiflow
docker-compose导入导出命令 涉及的命令有export.import.save.load save 命令 docker save [options] images [images...] ...
- Go语言学习的坑爹历程
鄙人暑期实习,需要用Go语言进行编程 在go语言中,结构体的定义只支持变量的声明,成员函数是采用"接口方法"来实现的 留一个成员定义的模板在此 package main impor ...
- 谷歌MapReduce经典论文翻译(中英对照)
MapReduce: Simplified Data Processing on Large Clusters(MapReduce: 简化大型集群下的数据处理) 作者:Jeffrey Dean and ...
- 创建Elasticsearch集群并为它们配置TLS安全通信
文章转载自:https://elasticstack.blog.csdn.net/article/details/105636302 文章开头讲述的是两台es主机构建一个集群,其中有关的配置可以借鉴 ...
- 查看pod创建时使用yaml文件内容
除了 kubectl describe pod 以外,另一种获取 Pod 额外信息(除了 kubectl get pod)的方法 是给 kubectl get pod 增加 -o yaml 输出格式参 ...
- CentOS 7.7系统安装Redis 6.0.3
前提操作 避免出现如下的错误 yum -y install gcc tcl yum -y install centos-release-scl yum -y install devtoolset-9- ...
- DevOps图示
- Springboot 之 HandlerMethodReturnValueHandler 运用
简介 现在项目中大部分采用前后端分离的架构,采用这种架构的项目,在返回数据时,几乎都是采用返回 json 格式的数据.而 spring 中返回 json 格式的数据一般采用 @RestControll ...
- GitLab + Jenkins + Harbor 工具链快速落地指南
目录 一.今天想干啥? 二.今天干点啥? 三.今天怎么干? 3.1.常规打法 3.2.不走寻常路 四.开干吧! 4.1.工具链部署 4.2.网络配置 4.3.验证工具链部署结果 4.3.1.GitLa ...
