Leetcode 799.香槟塔：动态规划+递归

香槟塔：动态规划+递归

题目来源：Leetcode 22/11/20每日一题：799.香槟塔

https://leetcode.cn/problems/champagne-tower

我们把玻璃杯摆成金字塔的形状，其中 第一层 有 1 个玻璃杯， 第二层 有 2 个，依次类推到第 100 层，每个玻璃杯 (250ml) 将盛有香槟。
从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）
例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟。
现在当倾倒了非负整数杯香槟后，返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例（ i 和 j 都从0开始）。

示例 1:
输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.00000
解释: 我们在顶层（下标是（0，0））倒了一杯香槟后，没有溢出，因此所有在顶层以下的玻璃杯都是空的。

示例 2:
输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.50000
解释: 我们在顶层（下标是（0，0）倒了两杯香槟后，有一杯量的香槟将从顶层溢出，位于（1，0）的玻璃杯和（1，1）的玻璃杯平分了这一杯香槟，所以每个玻璃杯有一半的香槟。
示例 3:

输入: poured = 100000009, query_row = 33, query_glass = 17
输出: 1.00000

解释

因为下层杯子中的量是从上层溢出的，即与上层有关的。很自然的会想到dp。

如何定义dp数组？只需一个一维数组即可，长度为0~要查询的杯子的位置。要查询的杯子的位置是什么？观察香槟塔的摆放方式，可以看到，第一层1个杯子，第二层2个杯子...第n层n个杯子，每层杯子数量构成了一个等差数列，那么计算要查询的杯子位置，只需计算它所在层数前的所有层的杯子总数+它在本层中所在的位置即可：

\(dp[i], 0 <= i <= (query\_row * (query\_row + 1) / 2 + query\_glass + 1)\)

下面，只需要按照层级来进行dfs即可，边界条件是：

• 当前层<最大层（即目标杯子所在的层）：递归
• 当前层=最大层：结束递归

对于每一层，需要从这一层的杯子开始位置，一直遍历到杯子结束的位置。某一层杯子开始位置是：\(curStart = cur * (cur + 1) / 2\)，每一层的杯子个数是：\(cur+1\)，其中\(cur\)表示当前所在的层数，\(cur\)从0开始。

对于某一层的某一个杯子，假设其所在层数的起始坐标为\(curStart\)，它位于所在层的第\(i\)个位置（\(i\)从0开始），进行如下处理：

• 如果\(dp[curStart + i]> 1.0\)，那么该杯子中的香槟会溢出，此时记录溢出值：\(more = dp[curStart + i] - 1.0\)，并将该杯子的香槟量设置为1。
• 对于溢出的香槟more，应该平分给其下层的两个“孩子”。

如何确定两个孩子的坐标？观察可得，如果一个杯子在某一层的第\(i\)个位置，那么它的孩子在其下一层的第\(i\)个位置和第\(i+1\)个位置。

如下图，以2号为例，其孩子为4号和5号，2号位于第1层（层数从0开始）的第1个（位置从0开始）位置，而4号位于第2层的第1个位置，5号位于第2层的第2个位置。

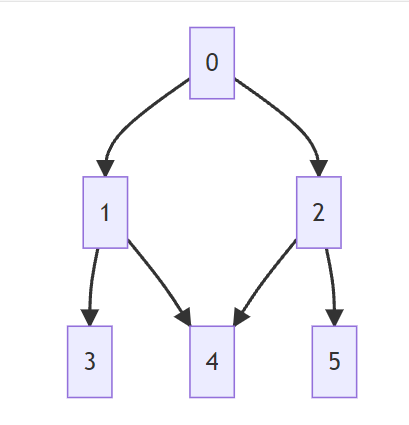
那么数值上就容易确定了，假设当前节点位于第\(cur\)层的第\(i\)个，那么其两个孩子的坐标分别为：

\(leftChild = (cur + 2) * (cur + 1) / 2 + i\)，

\(rightChild = leftChild + 1\)。

确定了两个孩子坐标后，只需要将\(more\)平分给两个孩子即可。别忘记判断孩子坐标是否越界。

实现

代码如下：

/**
 * 时间2ms，超过98.42%
 * 空间41.6MB，超过93.69%
 */
class Solution {
    public double champagneTower(int poured, int query_row, int query_glass) {
        int n = query_row * (query_row + 1) / 2 + query_glass + 1;
        double[] dp = new double[n];
        dp[0] = poured;
        cal(dp, query_row, 0);
        return Math.min(dp[n-1], 1.0);
    }

    public void cal(double[] dp, int max, int cur) {
        if(cur < max) {
            int curStart = cur * (cur + 1) / 2;
            for(int i = 0; i <= cur; ++i) {
                if(dp[i + curStart] > 1.0) {
                    double more = dp[i + curStart] - 1.0;
                    dp[i + curStart] = 1.0;
                    int leftChild = (cur + 2) * (cur + 1) / 2 + i;
                    int rightChild = leftChild + 1;
                    if(leftChild < dp.length) dp[leftChild] += more / 2;
                    if(rightChild < dp.length) dp[rightChild] += more / 2;
                }
            }
            cal(dp, max, cur + 1);
        }
    }
}

复杂度分析

时间复杂度O(n)，需要遍历一遍杯子；空间复杂度O(n)，需要一个dp数组和递归所用到的栈。