逻辑回归（LR）总结复习

摘要：

　　1.算法概述

　　2.算法推导

　　3.算法特性及优缺点

　　4.注意事项

　　5.实现和具体例子

　　6.适用场合

内容：

1.算法概述

　　最基本的LR分类器适合于对两分类（类0，类1）目标进行分类；这个模型以样本特征的线性组合sigma(theta * Xi)作为自变量，使用logistic函数将自变量映射到(0,1)上。

　　其中logistic函数（sigmoid函数为）：

　　

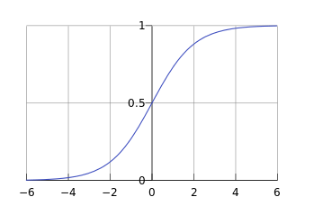
　　函数图形为：

　　

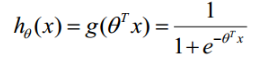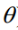　　　从而得到LR的模型函数为：，其中待定。

2.算法（数学）推导

　　建立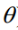的似然函数：

　　

　　对上述函数求对数：

　　做下函数变换：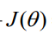

　　

　　通过梯度下降法求最小值。θ的初始值可以全部为1.0，更新过程为：（j表样本第j个属性，共n个；a表示步长--每次移动量大小，可自由指定）

　　 求导：

　　

　　

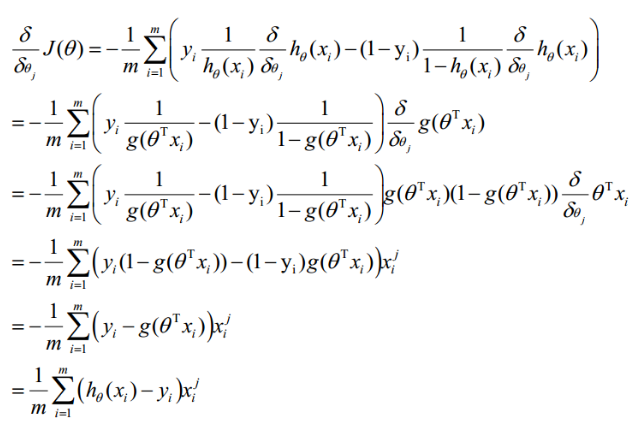
　　因此，θ（可以设初始值全部为1.0）的更新过程可以写成：

　　（i表示第i个统计样本，j表样本第j个属性；a表示步长）

　　矩阵形式（矢量化）的解：

　　

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知hθ(x)-y可由g(A)-y一次计算求得。

θ更新过程可以改为：

综上所述，Vectorization后θ更新的步骤如下：

（1）求A=X*θ(此处为矩阵乘法，X是（m,n+1）维向量，θ是（n+1，1）维列向量，A就是（m,1）维向量)

（2）求E=g(A)-y（E、y是（m,1）维列向量）

（3）求 （a表示步长）

3.算法特性及优缺点

　　 LR分类器适用数据类型：数值型和标称型数据。

　　 可用于概率预测，也可用于分类。

　　其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。

　　各feature之间不需要满足条件独立假设(相比NB)，但各个feature的贡献是独立计算的(相比DT)。

4.注意事项

　　步长a的选择：值太小则收敛慢，值太大则不能保证迭代过程收敛（迈过了极小值）。

　　归一化：多维特征的训练数据进行回归采取梯度法求解时其特征值必须做scale，确保特征的取值范围在相同的尺度内计算过程才会收敛

　　最优化方法选择：L-BFGS，收敛速度快；（这个不太懂）

　　正则化：L1正则化可以选择特征，去除共线性影响；损失函数中使用了L1正则化，避免过拟合的同时输出稀疏模型；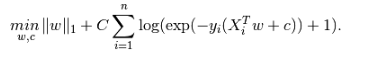

　　(来自http://scikit-learn.org/stable/modules/linear_model.html#logistic-regression)

5.实现和具体例子

　　Logistic回归的主要用途：

• 寻找危险因素：寻找某一疾病的危险因素等；

• 预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；

• CTR预测：http://www.flickering.cn/uncategorized/2014/10/转化率预估-2逻辑回归技术/?utm_source=tuicool&utm_medium=referral
• 官网使用LR L1正则项进行特征选择的例子：https://github.com/Tongzhenguo/Python-Project/blob/master/learntoscikit/LRforFeatureSelect.py
• 一个银行风控的例子：http://www.weixinla.com/document/44745246.html

6.适用场合

　　是否支持大规模数据：支持，并且有分布式实现

　　特征维度：可以很高

　　是否有 Online 算法:有（参考自）

　　特征处理：支持数值型数据，类别型类型需要进行0-1编码