TopCoder SRM 682 Div1 Problem 450 SuccessfulMerger （环套树 + 分类讨论）

题意  给定一个$n$个点$n$条边的无向图，现在要把这个图进行若干次操作，并选择一个点作为首都。

　　 要求除首都外的任意两个点$u$, $v$，从$u$走到$v$必须经过这个首都。

操作为合并两个相邻的点为一个点，即把这两个点从原图中删除，连接这两个点的边接到新的点上去。

考虑最后这个图的形态其实是一个菊花图，那么可以考虑到最后剩下的这些点其实只有选出的首都和

原图中度数为$1$的点。

但是有这么一种比较特殊的情况。

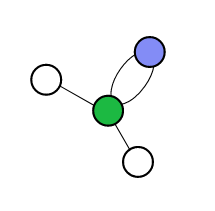
这个图也是符合题意的。

原来的图其实是一个环套树（环的大小可能为$2$）

如果这个环上存在一个度数为$2$的点（即除了和环上的点相连之外其他没有点和他相连）

那么这个点也可以被留下，但是所有这样的点中最多只能留下一个。

于是答案就很显然了。

#include <bits/stdc++.h>

using namespace std;

#define rep(i, a, b)	for (int i(a); i <= (b); ++i)
#define dec(i, a, b)	for (int i(a); i >= (b); --i)
#define MP		make_pair

typedef long long LL;
typedef pair <int, int> PII;

const int N = 105;

int vis[N], father[N], isroot[N], a[N];
int cnt;
int flag;
int n, now, ans;
int xx, yy;
map <PII, int> mp;
vector <int> v[N];

int get_circle(int x){
	vis[x] = 1;
	for (auto u : v[x]){
		if (u == father[x]) continue;
		father[u] = x;
		if (vis[u]){
			cnt = 0;
			int w = x;
			while (w ^ u){
				a[++cnt] = w;
				isroot[w] = cnt;
				w = father[w];
			}

			a[++cnt] = u;
			isroot[u] = cnt;
			return 1;
		}

		if (get_circle(u)) return 1;
	}

	return 0;
}

void dfs(int x){
	vis[x] = 1;
	for (auto u : v[x]){
		if (vis[u] || isroot[u]) continue;
		dfs(u);
	}
}

class SuccessfulMerger{
	public:
		int minimumMergers(vector<int> road){
			memset(a, 0, sizeof a);
			memset(isroot, 0, sizeof isroot);
			memset(father, 0, sizeof father);
			memset(vis, 0, sizeof vis);
			cnt = 0;
			n = 0;
			flag = 0;
			mp.clear();
			rep(i, 0, 100) v[i].clear();
			for (auto u : road){
				++n;
				++u;
				int x = n, y = u;
				if (x > y) swap(x, y);
				if (mp.count(MP(x, y))){
					flag = 1;
					xx = x, yy = y;
					continue;
				}

				mp[MP(x, y)] = 1;
				v[x].push_back(y);
				v[y].push_back(x);
			}

			if (flag){
				cnt = 2;
				a[1] = xx;
				a[2] = yy;
			}

			else get_circle(1);

			if (flag){
				v[xx].push_back(yy);
				v[yy].push_back(xx);
			}

			ans = n - 1;
			rep(i, 1, n) if ((int)v[i].size() == 1) --ans;

			rep(i, 1, cnt){
				int ccc = 0;
				for (auto u : v[a[i]]){
					int fg = 0;
					rep(j, 1, cnt) if (u == a[j]) fg = 1;
					if (fg == 0) ccc = 1;
				}

				if (ccc == 0){ --ans; break; }
			}

			return ans;
		}
};