svg path中的贝塞尔曲线

首先介绍以下什么是贝塞尔曲线

贝塞尔曲线又叫贝茨曲线（Bezier），由两个端点以及若干个控制点组成，只有两个端点在曲线上，控制点不在曲线上，只是控制曲线的走向。

控制点个数为0时，它是一条直线;

控制点个数为1时，它是二次贝塞尔曲线;

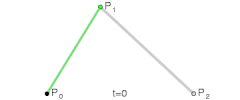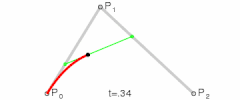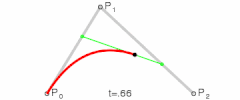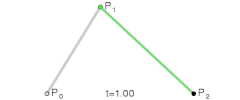
控制点个数为2时，它是三次贝塞尔曲线；

....

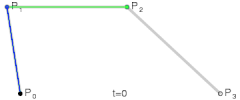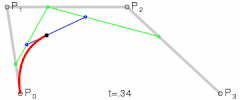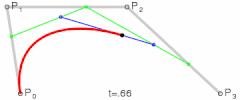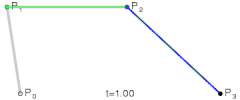
数学公式

二次贝塞尔曲线

p0,p2是起始点，p1是控制点

分别把p0,p1,p2点的x,y坐标带入，求出曲线上的点的x,y坐标

三次贝塞尔曲线

p0,p3是起始点，p1,p2是控制点

svg的path中与贝塞尔曲线相关的命令有：

C(curveto):三次贝塞尔曲线，参数：
x1,y1 x2,y2 m,n

x1,y1 x2,y2为两个控制点的xy坐标，m n为终点的坐标，起始点为执行该命令之前，笔触的位置。（注：svg中的曲线命令通常与M命令一起使用）

S(smooth curveto)参数：

x2,y2 m,n

x2,y2为第二个控制点，m n为终点的坐标,对于第一个控制点分为两种情况：

当S命令的前一个命令是C或S命令时，第一个控制点是前一个C或S的控制点的对称点（关于前一个命令的终点或当前命令的起始点）；

否则S命令将退化为二次贝塞尔曲线（同Q）。

Q(quadratic Belzier c

urve)二次贝塞尔曲线，参数：

x1,y1 m,n

x1,y1为控制点坐标，m,n为终点坐标。

T(smooth quadratic Belzier curveto)

参数：m,n

同S相似，T是Q的退化或者懒人写法。分为两种情况：

当T的前一个命令是Q或T时，控制点是前一个Q或T的控制点的对称点（关于前一个命令的终点或当前命令的起始点）；否则T命令将退化为一条直线。

相对坐标

c,s,q,t命令的相对位移相对的是同一个点，

以c命令为例，当pen表示当前笔触的位置时，

点的绝对坐标为：

x1=pen[0]+dx1

y1=pen[1]+dy1

x2=pen[0]+dx2

y2=pen[1]+dy2

m=pen[0]+mx

n=pen[1]+my

参考：https://zh.wikipedia.org/zh-cn/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A

http://www.zhangxinxu.com/wordpress/2014/06/deep-understand-svg-path-bezier-curves-command/