拓扑排序(二)之 C++详解

本章是通过C++实现拓扑排序。

目录
1. 拓扑排序介绍
2. 拓扑排序的算法图解
3. 拓扑排序的代码说明
4. 拓扑排序的完整源码和测试程序

转载请注明出处：http://www.cnblogs.com/skywang12345/

更多内容：数据结构与算法系列 目录

拓扑排序介绍

拓扑排序(Topological Order)是指，将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。

这样说，可能理解起来比较抽象。下面通过简单的例子进行说明！
例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。现在要制定一个计划，写出A、B、C、D的执行顺序。这时，就可以利用到拓扑排序，它就是用来确定事物发生的顺序的。

在拓扑排序中，如果存在一条从顶点A到顶点B的路径，那么在排序结果中B出现在A的后面。

拓扑排序的算法图解

拓扑排序算法的基本步骤：

1. 构造一个队列Q(queue) 和 拓扑排序的结果队列T(topological)；
2. 把所有没有依赖顶点的节点放入Q；
3. 当Q还有顶点的时候，执行下面步骤：
3.1 从Q中取出一个顶点n(将n从Q中删掉)，并放入T(将n加入到结果集中)；
3.2 对n每一个邻接点m(n是起点，m是终点)；
3.2.1 去掉边<n,m>;
3.2.2 如果m没有依赖顶点，则把m放入Q;
注：顶点A没有依赖顶点，是指不存在以A为终点的边。

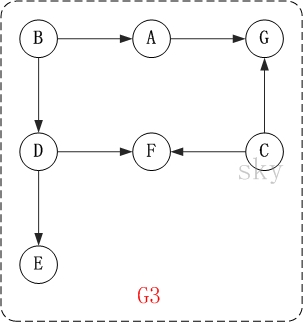
以上图为例，来对拓扑排序进行演示。

第1步：将B和C加入到排序结果中。
    顶点B和顶点C都是没有依赖顶点，因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储，因此先访问B，再访问C。访问B之后，去掉边<B,A>和<B,D>，并将A和D加入到队列Q中。同样的，去掉边<C,F>和<C,G>，并将F和G加入到Q中。
    (01) 将B加入到排序结果中，然后去掉边<B,A>和<B,D>；此时，由于A和D没有依赖顶点，因此并将A和D加入到队列Q中。
    (02) 将C加入到排序结果中，然后去掉边<C,F>和<C,G>；此时，由于F有依赖顶点D，G有依赖顶点A，因此不对F和G进行处理。
第2步：将A,D依次加入到排序结果中。
    第1步访问之后，A,D都是没有依赖顶点的，根据存储顺序，先访问A，然后访问D。访问之后，删除顶点A和顶点D的出边。
第3步：将E,F,G依次加入到排序结果中。

因此访问顺序是：B -> C -> A -> D -> E -> F -> G

拓扑排序的代码说明

拓扑排序是对有向无向图的排序。下面以邻接表实现的有向图来对拓扑排序进行说明。

1. 基本定义

#define MAX 100
// 邻接表
class ListDG
{
    private: // 内部类
        // 邻接表中表对应的链表的顶点
        class ENode
        {
            int ivex;           // 该边所指向的顶点的位置
            ENode *nextEdge;    // 指向下一条弧的指针
            friend class ListDG;
        };

        // 邻接表中表的顶点
        class VNode
        {
            char data;          // 顶点信息
            ENode *firstEdge;   // 指向第一条依附该顶点的弧
            friend class ListDG;
        };

    private: // 私有成员
        int mVexNum;             // 图的顶点的数目
        int mEdgNum;             // 图的边的数目
        VNode *mVexs;            // 图的顶点数组

    public:
        // 创建邻接表对应的图(自己输入)
        ListDG();
        // 创建邻接表对应的图(用已提供的数据)
        ListDG(char vexs[], int vlen, char edges[][2], int elen);
        ~ListDG();

        // 深度优先搜索遍历图
        void DFS();
        // 广度优先搜索（类似于树的层次遍历）
        void BFS();
        // 打印邻接表图
        void print();
        // 拓扑排序
        int topologicalSort();

    private:
        // 读取一个输入字符
        char readChar();
        // 返回ch的位置
        int getPosition(char ch);
        // 深度优先搜索遍历图的递归实现
        void DFS(int i, int *visited);
        // 将node节点链接到list的最后
        void linkLast(ENode *list, ENode *node);
};

(01) ListDG是邻接表对应的结构体。 mVexNum是顶点数，mEdgNum是边数；mVexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。 data是顶点所包含的数据，而firstEdge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。 ivex是该节点所对应的顶点在vexs中的索引，而nextEdge是指向下一个节点的。

2. 拓扑排序

/*
 * 拓扑排序
 *
 * 返回值：
 *     -1 -- 失败(由于内存不足等原因导致)
 *      0 -- 成功排序，并输入结果
 *      1 -- 失败(该有向图是有环的)
 */
int ListDG::topologicalSort()
{
    int i,j;
    int index = 0;
    int head = 0;           // 辅助队列的头
    int rear = 0;           // 辅助队列的尾
    int *queue;             // 辅组队列
    int *ins;               // 入度数组
    char *tops;             // 拓扑排序结果数组，记录每个节点的排序后的序号。
    ENode *node;

    ins   = new int[mVexNum];
    queue = new int[mVexNum];
    tops  = new char[mVexNum];
    memset(ins, 0, mVexNum*sizeof(int));
    memset(queue, 0, mVexNum*sizeof(int));
    memset(tops, 0, mVexNum*sizeof(char));

    // 统计每个顶点的入度数
    for(i = 0; i < mVexNum; i++)
    {
        node = mVexs[i].firstEdge;
        while (node != NULL)
        {
            ins[node->ivex]++;
            node = node->nextEdge;
        }
    }

    // 将所有入度为0的顶点入队列
    for(i = 0; i < mVexNum; i ++)
        if(ins[i] == 0)
            queue[rear++] = i;          // 入队列

    while (head != rear)                // 队列非空
    {
        j = queue[head++];              // 出队列。j是顶点的序号
        tops[index++] = mVexs[j].data;  // 将该顶点添加到tops中，tops是排序结果
        node = mVexs[j].firstEdge;      // 获取以该顶点为起点的出边队列

        // 将与"node"关联的节点的入度减1；
        // 若减1之后，该节点的入度为0；则将该节点添加到队列中。
        while(node != NULL)
        {
            // 将节点(序号为node->ivex)的入度减1。
            ins[node->ivex]--;
            // 若节点的入度为0，则将其"入队列"
            if( ins[node->ivex] == 0)
                queue[rear++] = node->ivex;  // 入队列

            node = node->nextEdge;
        }
    }

    if(index != mVexNum)
    {
        cout << "Graph has a cycle" << endl;
        delete queue;
        delete ins;
        delete tops;
        return 1;
    }

    // 打印拓扑排序结果
    cout << "== TopSort: ";
    for(i = 0; i < mVexNum; i ++)
        cout << tops[i] << " ";
    cout << endl;

    delete queue;
    delete ins;
    delete tops;

    return 0;
}

说明：
(01) queue的作用就是用来存储没有依赖顶点的顶点。它与前面所说的Q相对应。
(02) tops的作用就是用来存储排序结果。它与前面所说的T相对应。

拓扑排序的完整源码和测试程序

拓扑排序源码(ListDG.cpp)