Expm 3_2 寻找最邻近的点对

 

【问题描述】

设p₁=(x₁,y₁), p₂=(x₂,y₂), … , p_n=(x_n,y_n) 是平面上n个点构成的集合S，设计和实现找出集合S中距离最近点对的算法。

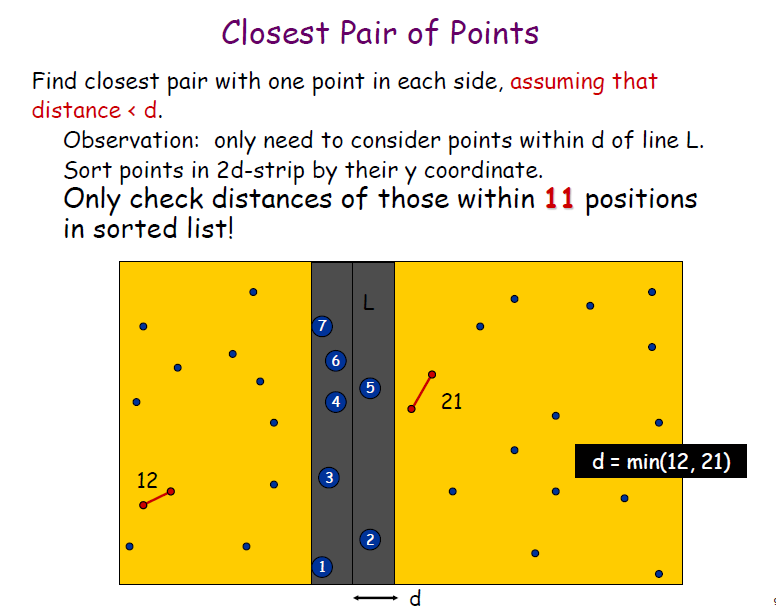
　　每一个格子最多只能存在一个点,三行最多存在12个顶点，因此对于上图中的第(i=27)个顶点来说，最多只需要比较第27个顶点与之后的11个顶点，对于i之后或之前的11个顶点之外的顶点j，即|i-j|>=12,i与j之间的距离一定大于d，因为i和j已经相隔了至少两行。两个顶点若相隔大于等于两行或两列，则他们之间的距离一定大于等于d

 package org.xiu68.exp.exp3;

 import java.util.ArrayList;
 import java.util.List;
 import java.util.Random;

 public class Exp3_2 {

     //设p1=(x1,y1), p2=(x2,y2), … , pn=(xn,yn)
     //是平面上n个点构成的集合S，设计和实现找出集合S中距离最近点对的算法。
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         for(int i=0;i<20;i++){
             System.out.println("***************************");
             List<Point> pointList=new ArrayList<>();
             for(int j=0;j<50;j++){
                 Point p=new Point(new Random().nextInt(100),new Random().nextInt(100));
                 pointList.add(p);
             }
             System.out.println(bruteforce(pointList));        //蛮力法
             System.out.println(closestPair(pointList));        //分治法

             System.out.println("****************************");
         }
     }

     //寻找最近点对
     public static double closestPair(List<Point> pointList){
         //对pointList中的点按横坐标和纵坐标进行升序排序

         List<Point> sortedListX=new ArrayList<>();
         List<Point> sortedListY=new ArrayList<>();    

         //按横坐标对数组进行升序排序
         pointList.sort((Point a,Point b)->{
             if(a.getX()<b.getX())
                 return -1;
             else
                 return 1;
         });
         sortedListX.addAll(pointList);

         //按纵坐标对数组进行升序排序
         pointList.sort((Point a,Point b)->{
             if(a.getY()<b.getY())
                 return -1;
             else
                 return 1;
         });
         sortedListY.addAll(pointList);

 /*        for(int i=0;i<pointList.size();i++)
             System.out.println(sortedListX.get(i));
         System.out.println("*********************");
         for(int i=0;i<pointList.size();i++)
             System.out.println(sortedListY.get(i));

         System.out.println("*********************");
         System.out.println(divide(sortedListX,sortedListY));*/

         return divide(sortedListX,sortedListY);

     }

     /*
      * 原问题的分解
      * sortedListX:横坐标升序排序的数组
      * sortedListY:纵坐标升序排序的数组
      */
     public static double divide(List<Point> sortedListX,List<Point> sortedListY){
         if(sortedListX.size()==1)        //如果只有一个元素
             return Double.MAX_VALUE;
         else if(sortedListX.size()==2)    //如果只有两个元素
             return dist(sortedListX.get(0),sortedListX.get(1));

         else{                            //大于2个元素
             int mid=sortedListX.size()/2;                //在第mid个点处把点分成左右相等的两部分
             double L=sortedListX.get(mid).getX();    //把点分成左右相等的两部分的直线的横坐标，设这条直线为L

             //L左边的点的横坐标升序排序的数组
             List<Point> sortedListXL=sortedListX.subList(0, mid);    

             //L右边的点的横坐标升序排序的数组
             List<Point> sortedListXR=sortedListX.subList(mid, sortedListX.size());

             List<Point> sortedListYL=new ArrayList<>();        //L左边的点的纵坐标升序排序的数组
             List<Point> sortedListYR=new ArrayList<>();        //L右边的点的纵坐标升序排序的数组

             //求sortedListYL与sortedListYR
             for(int i=0;i<sortedListY.size();i++){
                 Point p=sortedListY.get(i);
                 if(sortedListY.get(i).getX()<L){
                     sortedListYL.add(p);
                 }else{
                     sortedListYR.add(p);
                 }
             }

             double dL=divide(sortedListXL,sortedListYL);    //L左边两个点之间的最短距离
             double dR=divide(sortedListXR,sortedListYR);    //L右边两个点之间的最短距离

             //比较L左边最短距离、L右边最短距离以及跨越L的顶点对之间的最短距离
             return conquer(sortedListY,L,Math.min(dL, dR));
         }//else
     }

     //子问题解的合并
     public static double conquer(List<Point> sortedListY,double L,double d){
         //求在L-d以及L+d之间的顶点(2d-strip)
         List<Point> inside2DList=new ArrayList<>();
         for(int i=0;i<sortedListY.size();i++){
             Point p=sortedListY.get(i);
             if(p.getX()>L-d || p.getX()<L+d){
                 inside2DList.add(p);
             }
         }

         //求2d-strip之间顶点对的最短距离、与L左边和右边的最短距离比较，最小者为最终结果
         double minDistance=d;
         for(int i=0;i<inside2DList.size()-1;i++){
             //i只需与i之后的11个顶点比较，i与大于11个顶点之后的顶点的距离一定大于等于d
             for(int j=i+1;j<=i+11 && j<inside2DList.size();j++){
                 double temp=dist(inside2DList.get(i),inside2DList.get(j));
                 if(temp<minDistance)
                     minDistance=temp;
             }
         }
         return minDistance;
     }

     //计算两点之间的距离
     public static double dist(Point a,Point b){
         return Math.sqrt(Math.pow(a.getX()-b.getX(), 2)+Math.pow(a.getY()-b.getY(), 2));
     }

     //蛮力法
     public static double bruteforce(List<Point> pointList){
         double minDistance=Double.MAX_VALUE;
         //依次比较每个顶点对
         for(int i=0;i<pointList.size();i++){
             for(int j=i+1;j<pointList.size();j++){
                 double temp=dist(pointList.get(i),pointList.get(j));
                 if(temp<minDistance)
                     minDistance=temp;
             }
         }
         return minDistance;
     }
 }

 class Point{
     private double x;        //横坐标
     private double y;        //纵坐标

     public Point(int x,int y){
         this.x=x;
         this.y=y;
     }

     public double getX() {
         return x;
     }

     public void setX(double x) {
         this.x = x;
     }

     public double getY() {
         return y;
     }

     public void setY(double y) {
         this.y = y;
     }

     public String toString(){
         return x+","+y;
     }
 }