Codeforces 839C Journey - 树形动态规划 - 数学期望

There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.

Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.

Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the link https://en.wikipedia.org/wiki/Expected_value.

Input

The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.

Then n - 1 lines follow. The i-th line of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the cities connected by the i-th road.

It is guaranteed that one can reach any city from any other by the roads.

Output

Print a number — the expected length of their journey. The journey starts in the city 1.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .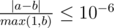

Examples

input

4
1 2
1 3
2 4

output

1.500000000000000

input

5
1 2
1 3
3 4
2 5

output

2.000000000000000

Note

In the first sample, their journey may end in cities 3 or 4 with equal probability. The distance to city 3 is 1 and to city 4 is 2, so the expected length is 1.5.

In the second sample, their journey may end in city 4 or 5. The distance to the both cities is 2, so the expected length is 2.

---

　　题目大意 给定一棵有n个节点的树，某个人骑着一匹等概率走向任意相连的未经过节点的马从1号点开始旅行，当到某个点的无法移动旅行结束。求期望的旅行长度(每条边的长度为1)。

　　显然到了某个点就不能到它的父节点。所以考虑动态规划。

　　f[i]表示当到达节点i后，期望还能走的步数。显然某个叶节点的f值为0.

　　现在考虑转移。

　　显然是每个子节点的f值加1再乘走到这个节点的概率。

Code

 /**
  * Codeforces
  * Problem#839C
  * Accepted
  * Time: 78ms
  * Memory: 11800k
  */
 #include <bits/stdc++.h>
 using namespace std;

 int n;
 vector<int> *g;
 double *f;

 inline void init() {
     scanf("%d", &n);
     g = new vector<int>[(n + )];
     f = new double[(n + )];
     for(int i = , u, v; i < n; i++) {
         scanf("%d%d", &u, &v);
         g[u].push_back(v);
         g[v].push_back(u);
     }
 }

 void dfs(int node, int fa) {
     f[node] = ;
     int count = ;
     for(int i = ; i < (signed)g[node].size(); i++)
         if(g[node][i] != fa)
             count++;
     if(!count)    return;
     double P = 1.0 / count;
     for(int i = ; i < (signed)g[node].size(); i++) {
         int& e = g[node][i];
         if(e == fa)    continue;
         dfs(e, node);
         f[node] += (f[e] + ) * P;
     }
 }

 inline void solve() {
     printf("%.12lf", f[]);
 }

 int main() {
     init();
     dfs(, );
     solve();
     return ;
 }