Neural Networks and Deep Learning 课程笔记(第四周)深层神经网络(Deep Neural Networks)
1. 深层神经网络(Deep L-layer neural network )


2. 前向传播和反向传播(Forward and backward propagation)



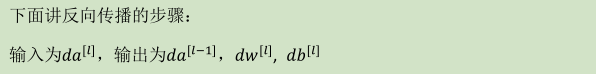

3. 总结


4. 深层网络中的前向传播(Forward propagation in a Deep Network)
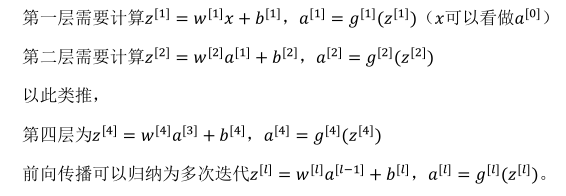

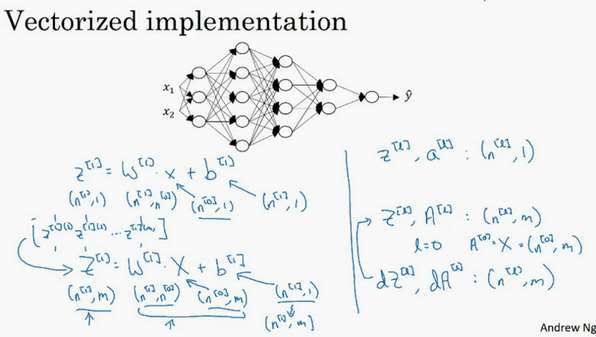
向量化实现过程可以写成:
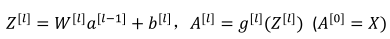
注:这里只能用一个显示for循环,l 从 1 到 L,然后一层接着一层去计算。
如何减少bug
4.1 核对矩阵的维数(Getting your matrix dimensions right)

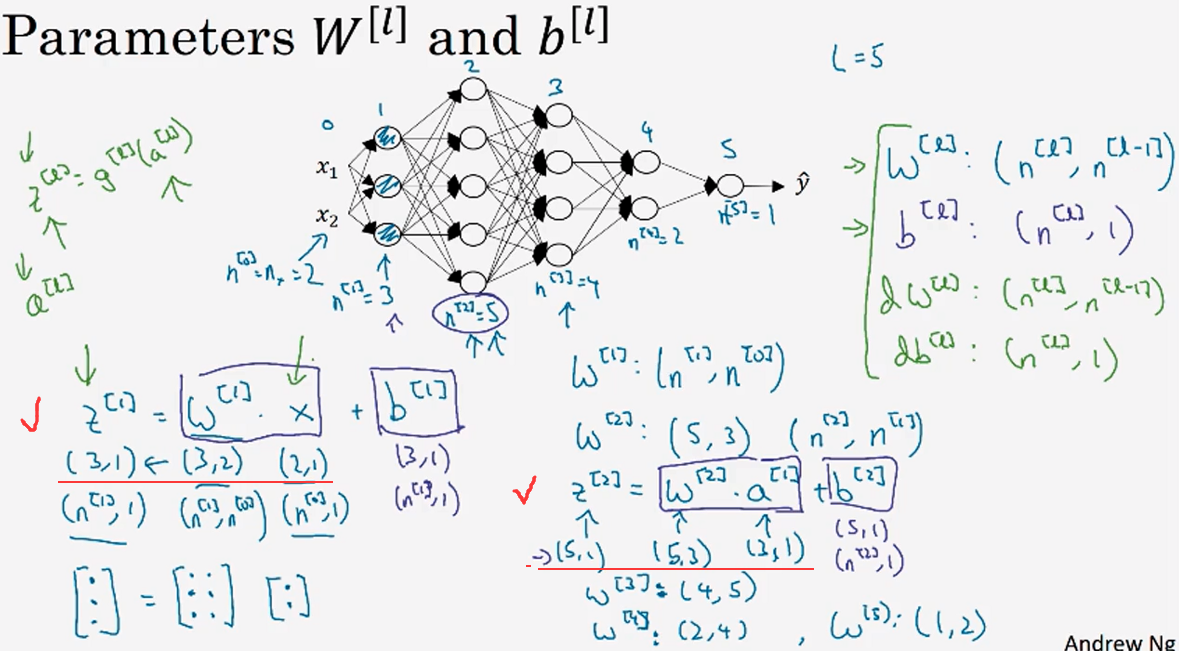
4.2 向量化实现

4.3 为什么使用深层表示?(Why deep representations? )
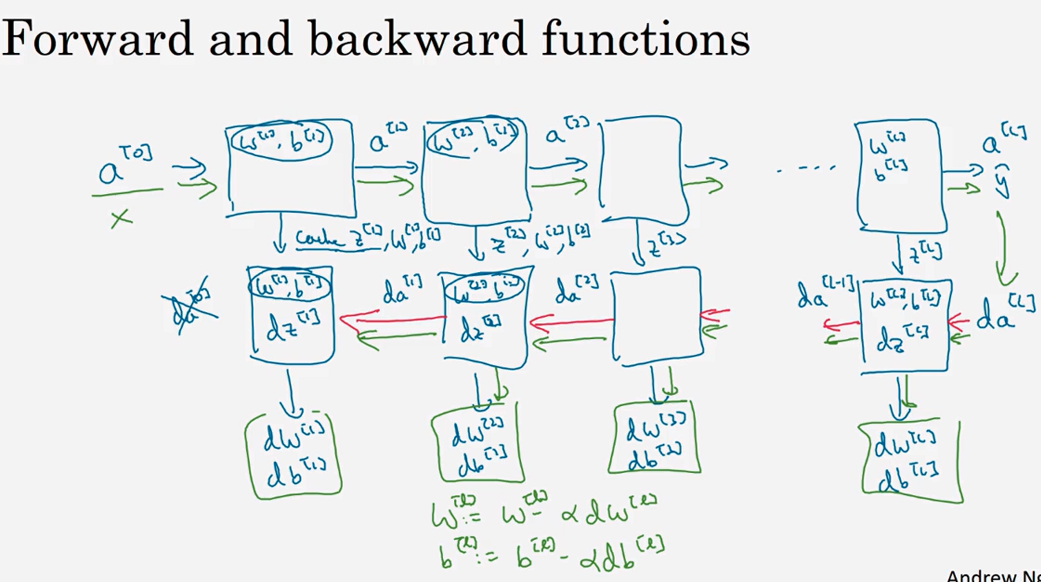
4.4 搭建神经网络块(Building blocks of deep neural networks)
4.5 参数 VS 超参数(Parameters vs Hyperparameters )

4.6 总结

Neural Networks and Deep Learning 课程笔记(第四周)深层神经网络(Deep Neural Networks)的更多相关文章
- Deep Learning论文笔记之(八)Deep Learning最新综述
Deep Learning论文笔记之(八)Deep Learning最新综述 zouxy09@qq.com http://blog.csdn.net/zouxy09 自己平时看了一些论文,但老感觉看完 ...
- 吴恩达《深度学习》-第二门课 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)-第一周:深度学习的实践层面 (Practical aspects of Deep Learning) -课程笔记
第一周:深度学习的实践层面 (Practical aspects of Deep Learning) 1.1 训练,验证,测试集(Train / Dev / Test sets) 创建新应用的过程中, ...
- AndrewNG Deep learning课程笔记 - CNN
参考, An Intuitive Explanation of Convolutional Neural Networks http://www.hackcv.com/index.php/archiv ...
- AndrewNG Deep learning课程笔记
神经网络基础 Deep learning就是深层神经网络 神经网络的结构如下, 这是两层神经网络,输入层一般不算在内,分别是hidden layer和output layer hidden layer ...
- 深度学习FPGA实现基础知识10(Deep Learning(深度学习)卷积神经网络(Convolutional Neural Network,CNN))
需求说明:深度学习FPGA实现知识储备 来自:http://blog.csdn.net/stdcoutzyx/article/details/41596663 说明:图文并茂,言简意赅. 自今年七月份 ...
- Neural Networks and Deep Learning 课程笔记(第三周)浅层神经网络(Shallow neural networks)
3.1 神经网络概述(Neural Network Overview ) (神经网络中,我们要反复计算a和z,最终得到最后的loss function) 3.2 神经网络的表示(Neural Netw ...
- Neural Networks and Deep Learning 课程笔记(第二周)神经网络的编程基础 (Basics of Neural Network programming)
总结 一.处理数据 1.1 向量化(vectorization) (height, width, 3) ===> 展开shape为(heigh*width*3, m)的向量 1.2 特征归一化( ...
- AndrewNG Deep learning课程笔记 - RNN
The Unreasonable Effectiveness of Recurrent Neural Networks,http://karpathy.github.io/2015/05/21/rnn ...
- 【DeepLearning学习笔记】Coursera课程《Neural Networks and Deep Learning》——Week1 Introduction to deep learning课堂笔记
Coursera课程<Neural Networks and Deep Learning> deeplearning.ai Week1 Introduction to deep learn ...
随机推荐
- C#中byte[] 与string相互转化问题
using System; using System.IO; using System.Security.Cryptography; namespace ShareX.UploadersLib.Oth ...
- 日常工作--IIS修改增加最大数据库连接池
1. 在全局配置文件中的 GSPDbConfiguration 需要修改数据库连接池的连接上面都增加上节点: MaxPoolSize = "100" 效果 即可 因为产品增加了对O ...
- React 表单refs
<!DOCTYPE html><html><head lang="en"> <meta charset="UTF-8" ...
- Angular require(抄别的)
require参数的值可以用下面的前缀进行修饰,这会改变查找控制器时的行为:?如果在当前指令中没有找到所需要的控制器,会将null作为传给link函数的第四个参数.^如果添加了^前缀,指令会在上游的指 ...
- 关于一个常用的CheckBox样式
我们在使用CheckBox的时候,原始的样式有时不能满足我们的需求,这是我们就需要更改其模板,比如我们常用的一种,在播放器中“播放”.“暂停”按钮,其实这也是一种CheckBox,只不过我们只是修改了 ...
- jvm学习二:类加载器
前一节详细的聊了一下类的加载过程,本节聊一聊类的加载工具,类加载器 --- ClassLoader 本想自己写的,查资料的时候查到一篇大神的文章,写的十分详细 大家直接过去看吧http://blo ...
- 关于Spring MVC跨域
1.Sping MVC 3.X跨域 关于跨域问题,主要用的比较多的是cros跨域. 详细介绍请看https://developer.mozilla.org/zh-CN/docs/Web/HTTP/Ac ...
- Lodop打印条码二维码的一些设置
Lodop绘制条码图功能让条码打印变得很简单,客户端不用安装专门的条码字库,该函数格式如下:ADD_PRINT_BARCODE(Top,Left,Width,Height,BarCodeType,Ba ...
- gbk、utf-8、utf8mb4区别
1. 存储大小(1). GBK编码专门用来解决中文编码的,是双字节的.不论中英文都是双字节的.(2). UTF-8 编码是用以解决国际上字符的一种多字节编码,它对英文使用8位(即一个字节),中文使用2 ...
- ansible系列4-关闭ssh首次连接时提示
在ansible配置文件中找到 /etc/ansible/ansible.cfg 方法1 在配置文件中找到 了解到问题原因为,我们了解到进行ssh连接时,可以使用-o参数将StrictHostKeyC ...
