topcoder srm 683 div1

problem1 link

肯定存在相邻两堆满足不会存在任何操作在这两堆之间进行。然后就成为一条链，那么只需要维护链的前缀和即可判断当前堆和前一堆之间需要多少次操作。

problem2 link

对于两个数字$x,y,x<y$，如果$y$不是$x$的倍数，那么一定有$lcm(x,y)+gcd(x,y)>x+y$。不妨假设$x=p_{1}^{a_{1}}p_{2}^{b_{1}},y=p_{1}^{a_{2}}p_{2}^{b_{2}}$，其中$p_{1},p_{2}$是两个不同的素数且$a_{1}<a_{2},b_{1}>b_{2}$,那么$lcm(x,y)+gcd(x,y)-x-y=p_{1}^{a_{2}}p_{2}^{b_{1}}+p_{1}^{a_{1}}p_{2}^{b_{2}}-p_{1}^{a_{1}}p_{2}^{b_{1}}-p_{1}^{a_{2}}p_{2}^{b_{2}}=p_{1}^{a_{1}}p_{2}^{b_{2}}(p_{1}^{a_{2}-a_{1}}-1)(p_{2}^{b_{1}-b_{2}}-1)>0$

所以任意两个进行一次操作之后，也就是$\frac{n(n-1)}{2}$次操作后，肯定会有一个最大的数字，它的各个质因子的指数是最大的，或者说对于素数$p$这个数字的$p$的指数不小于其他$n-1$个数字的$p$的指数；下一次对除了最大数字的其余$n-1$个数字再每两个进行这样的操作后，这 $n-1$个数字中的最大值的各个质因子的指数都是次大的。依次进行到最后即可。

比如$n=3$，这些数字为$2^{5}3^{8}5^{1},2^{7}3^{0}5^{10},2^{3}3^{4}5^{4}$，那么最后变成了$2^{7}3^{8}5^{10},2^{5}3^{4}5^{4},2^{3}3^{0}5^{1}$。

problem3 link

首先，将每个点看作是$(x,y)=(\frac{a+b}{2},\frac{a-b}{2})$,那么每次移动就是$a+1$或者$a-1$,以及$b+1$或者$b-1$。并且$a,b$是独立的。

所以$E(x^{n}y^{m})=E((\frac{a+b}{2})^{n}(\frac{a-b}{2})^m)=\sum_{i=0}^{n}\sum_{j=0}^{m}C_{n}^{i}C_{m}^{j}\frac{(-1)^{m-j}}{2^{n+m}}E(a^{i+j})E(b^{n+m-i-i})$

设$(x_{0},y_{0})=(\frac{A+B}{2},\frac{A-B}{2})$

那么最后的每个位置对应的$a,b$都可以分别看作是关于$A,B$的多项式，即$a=f(A),b=g(B)$.所有的这些位置逐个去计算这个多项式有点多，但是可以直接去求所有的位置对应的$a,b$对应的多项式的和。

比如当$t=0$时：

其中$(x_{0},y_{0})=(4,3),(A,B)=(11,-3)$

那么答案为$h(A,B)=(\frac{A+B}{2})^{n}(\frac{A-B}{2})^{m}=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}A^{i+j}B^{n+m-i-j}$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}S_{0}(A,i+j)S_{0}(B,n+m-i-j)$

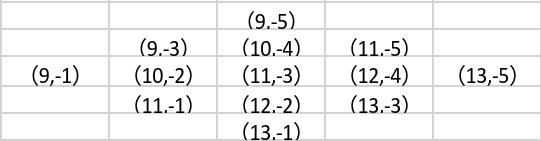
当$t=1$时(只画出了$(a,b)$)：

那么答案为$h(A-1,B-1)+h(A-1,B+1)+h(A+1,B-1)+h(A+1,B+1)$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}((A-1)^{i+j}+(A+1)^{i+j})((B-1)^{n+m-i-j}+(B+1)^{n+m-i-j})$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}(2\sum_{2|(i+j-t)}C_{i+j}^{t}A^{t})(2\sum_{2|(n+m-i-j-t)}C_{n+m-i-j}^{t}B^{t})$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}S_{1}(A,i+j)S_{1}(B,n+m-i-j)$

当$t=2$时：

答案为

$h((A-1)-1,(B-1)-1)+h((A-1)-1,(B-1)+1)+$

$h((A-1)+1,(B-1)-1)+h((A-1)+1,(B-1)+1)+$

$h((A-1)-1,(B+1)-1)+h((A-1)-1,(B+1)+1)+$

$h((A-1)+1,(B+1)-1)+h((A-1)+1,(B+1)+1)+$

$h((A+1)-1,(B-1)-1)+h((A+1)-1,(B-1)+1)+$

$h((A+1)+1,(B-1)-1)+h((A+1)+1,(B-1)+1)+$

$h((A+1)-1,(B+1)-1)+h((A+1)-1,(B+1)+1)+$

$h((A+1)+1,(B+1)-1)+h((A+1)+1,(B+1)+1)$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}([(A-1)-1]^{i+j}+[(A-1)+1]^{i+j}+[(A+1)-1]^{i+j}+[(A+1)+1]^{i+j})S_{2}(B,n+m-i-j)$

$=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}S_{2}(A,i+j)S_{2}(B,n+m-i-j)$

其中$S_{2}(A,i+j)=2\sum_{2|(i+j-t_{2})}C_{i+j}^{t_{2}}\left (  (A-1)^{t_{2}}+(A+1)^{t_{2}}\right )$

$2\sum_{2|(i+j-t_{2})}C_{i+j}^{t_{2}}\left (  2\sum_{2|(t_{2}-t_{1})}C_{t_{2}}^{t_{1}}A^{t_{1}}\right )$

从上面的推导可以看出，$S_{i}(A,j)$的递推公式为:$S_{i}(A,j)=2\sum_{2|(j-p)}C_{j}^{p}S_{i-1}(A,p)$

初始条件为$S_{0}(A,j)=A^{j}$.从而可以用矩阵快速幂计算出所有的$S_{t}(A,k),S_{t}(B,k)$

那么最后的答案为$r=\sum_{i=0}^{n}\sum_{j=0}^{m}\frac{(-1)^{m-j}}{2^{n+m}}S_{t}(A,i+j)S_{t}(B,n+m-i-j)$

code for problem1

#include <algorithm>
#include <limits>
#include <vector>

class MoveStones {
 public:
  long long get(const std::vector<int> &a, const std::vector<int> &b) {
    long long sum = 0;
    int n = static_cast<int>(a.size());
    for (int i = 0; i < n; ++i) {
      sum += a[i] - b[i];
    }
    if (sum != 0) {
      return -1;
    }
    if (n == 1) {
      return 0;
    }
    long long ans = std::numeric_limits<long long>::max();
    for (int i = 0; i < n; ++i) {
      long long pre = 0;
      long long tmp = 0;
      for (int j = 1; j <= n; ++j) {
        long long t = a[(i + j) % n] - b[(i + j) % n];
        tmp += std::abs(pre);
        pre += t;
      }
      ans = std::min(ans, tmp);
    }
    return ans;
  }
};

code for problem2

#include <algorithm>
#include <vector>

constexpr int kMaxN = 10000000;
constexpr int kMaxPrimeNum = 670000;
constexpr int kMod = 1000000007;

class GCDLCM2 {
 public:
  int getMaximalSum(const std::vector<int> &start, const std::vector<int> &d,
                    const std::vector<int> &cnt) {
    CreatePrimeTable();

    std::vector<std::vector<int>> f(kMaxPrimeNum);
    auto Add = [&](int x) {
      for (size_t i = 0; i < primes.size() && primes[i] * primes[i] <= x; ++i)
        if (x % primes[i] == 0) {
          int p = 1;
          while (x % primes[i] == 0) {
            p = p * primes[i];
            x /= primes[i];
          }
          f[i].push_back(p);
        }
      if (x != 1) {
        f[min_prime_indices[x]].push_back(x);
      }
    };

    std::vector<int> a;
    for (size_t i = 0; i < start.size(); ++i) {
      for (int j = 0; j < cnt[i]; ++j) {
        Add(start[i] + j * d[i]);
        a.push_back(1);
      }
    }
    int n = static_cast<int>(a.size());
    for (size_t i = 0; i < primes.size(); ++i) {
      if (!f[i].empty()) {
        int s = static_cast<int>(f[i].size());
        std::sort(f[i].begin(), f[i].end());
        for (int j = 0; j < s; ++j)
          a[n - s + j] =
              static_cast<int>(1ll * a[n - s + j] * f[i][j] % kMod);
      }
    }
    int sum = 0;
    for (int i = 0; i < n; ++i) {
      sum = (sum + a[i]) % kMod;
    }
    return sum;
  }

 private:
  std::vector<int> primes;
  std::vector<size_t> min_prime_indices;

  void CreatePrimeTable() {
    min_prime_indices.resize(kMaxN + 1);
    primes.reserve(kMaxPrimeNum);
    std::vector<bool> tag(kMaxN + 1);
    for (int i = 2; i <= kMaxN; ++i) {
      if (!tag[i]) {
        min_prime_indices[i] = primes.size();
        primes.push_back(i);
      }
      for (size_t j = 0; j < primes.size() && i * primes[j] <= kMaxN; ++j) {
        tag[i * primes[j]] = true;
        if (i % primes[j] == 0) {break;}
      }
    }
  }
};

code for problem3

#include <vector>

class RandomWalkOnGrid {
  static constexpr int kMod = 1000000007;

 public:
  int getExpectation(int x0, int y0, int t, int n, int m) {
    int total = n + m + 1;
    std::vector<std::vector<long long>> c(total, std::vector<long long>(total));
    c[0][0] = 1;
    for (int i = 1; i < total; ++i) {
      c[i][0] = c[i][i] = 1;
      for (int j = 1; j < i; ++j) {
        c[i][j] = Norm(c[i - 1][j - 1] + c[i - 1][j]);
      }
    }
    std::vector<std::vector<long long>> transform(
        total, std::vector<long long>(total, 0));
    for (int i = 0; i < total; ++i) {
      for (int j = 0; j <= i; ++j) {
        if ((i - j) % 2 == 0) {
          transform[j][i] = Norm(2 * c[i][j]);
        }
      }
    }
    transform = Pow(transform, t);
    std::vector<std::vector<long long>> pa(1, std::vector<long long>(total));
    std::vector<std::vector<long long>> pb(1, std::vector<long long>(total));
    int a = Norm((x0 + y0) % kMod);
    int b = Norm((x0 - y0) % kMod);
    for (int i = 0; i < total; ++i) {
      pa[0][i] = Pow(a, i);
      pb[0][i] = Pow(b, i);
    }
    pa = Multiply(pa, transform);
    pb = Multiply(pb, transform);
    long long result = 0;
    for (int i = 0; i <= n; ++i) {
      for (int j = 0; j <= m; ++j) {
        long long x = pa[0][i + j] * pb[0][n + m - i - j] % kMod;
        if ((m - j) % 2 == 1) {
          x = kMod - x;
        }
        Add(result, x * c[n][i] % kMod * c[m][j] % kMod);
      }
    }
    result = result * Reverse(Pow(2, n + m)) % kMod;
    return static_cast<int>(result);
  }

 private:
  std::vector<std::vector<long long>> Multiply(
      const std::vector<std::vector<long long>> &a,
      const std::vector<std::vector<long long>> &b) {
    int n = static_cast<int>(a.size());
    int m = static_cast<int>(b.size());
    int p = static_cast<int>(b[0].size());
    std::vector<std::vector<long long>> c(n, std::vector<long long>(p, 0));
    for (int i = 0; i < n; ++i) {
      for (int j = 0; j < p; ++j) {
        for (int k = 0; k < m; ++k) {
          Add(c[i][j], a[i][k] * b[k][j] % kMod);
        }
      }
    }
    return std::move(c);
  }

  std::vector<std::vector<long long>> Pow(std::vector<std::vector<long long>> a,
                                          int t) {
    int n = static_cast<int>(a.size());
    std::vector<std::vector<long long>> result(n, std::vector<long long>(n, 0));
    for (int i = 0; i < n; ++i) {
      result[i][i] = 1;
    }
    while (t > 0) {
      if (t % 2 == 1) {
        result = Multiply(result, a);
      }
      a = Multiply(a, a);
      t /= 2;
    }
    return std::move(result);
  }

  long long Pow(long long a, long long b) {
    long long result = 1;
    while (b > 0) {
      if (b % 2 == 1) {
        result = result * a % kMod;
      }
      a = a * a % kMod;
      b /= 2;
    }
    return result;
  }

  void Add(long long &x, long long y) {
    x += y;
    if (x >= kMod) {
      x -= kMod;
    }
  }

  long long Reverse(long long x) { return Pow(x, kMod - 2); }

  long long Norm(long long x) {
    if (x >= kMod) {
      x -= kMod;
    } else if (x < 0) {
      x += kMod;
    }
    return x;
  }
};

　

参考链接：

https://blog.csdn.net/PhilipsWeng/article/details/52318811