作业九——DFA最小化

1.将DFA最小化：教材P65 第9题

I	{1, 2, 3, 4, 5}	{6, 7}
	{1, 2}b->{1, 2, 3, 4, 5} {3, 4}b->{6, 7} {5}b-> {1, 2, 3, 4, 5}可区别，划分
II	{1, 2}{3, 4}{5}	{6, 7}
		{6}b->{6} {7}b->{6} {6, 7}不可区别，等价
III	{1, 2}{3, 4}{5}	{6, 7}
	{3}c->{3} {4}c->{4} {3}b->{6, 7} {4}b->{6, 7} {3}d->{5} {4}d->{5} {3, 4}不可区别，等价
IV	{1, 2}{3, 4}{5}	{6, 7}
	{1}a->{3, 4} {2}a->{3, 4} {1}b->{2} {2}b->{2} {1, 2}不可区别，等价

　　

　　状态转换图如下：

　　　

2.构造以下文法相应的最小的DFA

S→ 0A|1B

A→ 1S|1

B→0S|0

答：S -> 0A | 1B

　　　-> 0(1S | 1) | 1(0S | 0)

　　　-> 01S | 01 | 10S | 10

　　    -> (01 | 10)S | (01 | 10)

　　　-> (01 | 10)*(01 | 10)

　　由正规式可得NFA：

　　

　　由NFA可得DFA状态转换矩阵如下：

　　

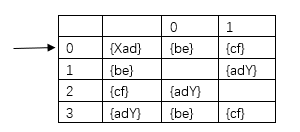
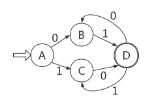
　　DFA状态转换图如下：

　　

　　最小化DFA如下：

　　

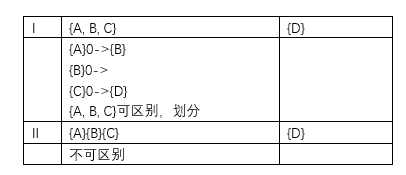
　　状态转换图如下：

　　 

3.自上而下语法分析，回溯产生的原因是什么？

　　文法中，对于某个非终结符的规则其右部有多个选择项，当根据所面临的输入符号不能准确的确定所要的选择项时，就可能出现回溯。

4.P100 练习4，反复提取公共左因子。

S -> C$

C -> bA | aB

A -> a | aC | bBB

B -> b | bC | aBB

答：S -> C$

　　C -> bA | aB

　　A -> aD | bAA

　　B -> bD | aBB

　　D -> ɛ | C