EM 算法(三)-GMM

高斯混合模型

混合模型，顾名思义就是几个概率分布密度混合在一起，而高斯混合模型是最常见的混合模型；

GMM，全称 Gaussian Mixture Model，中文名高斯混合模型，也就是由多个高斯分布混合起来的模型；

概率密度函数为

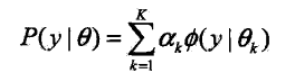
K 表示高斯分布的个数，α_k 表示每个高斯分布的系数，α_k>0，并且 Σα_k=1，

Ø(y|θ_k) 表示每个高斯分布，θ_k 表示每个高斯分布的参数，θ_k=(u_k，σ_k²)；

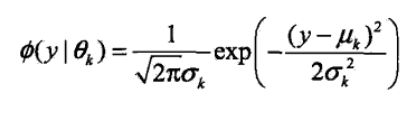
举个例子

男人和女人的身高都服从各自的高斯分布，把男人女人混在一起，那他们的身高就服从高斯混合分布；

高斯混合模型就是用混合在一起的身高数据，估计男人和女人各自的高斯分布

小结

GMM 实际上分为两步，第一步是选择一个高斯分布，如男人数据集，这里涉及取到某个分布的概率，α_k，

然后从该分布中取一个样本，等同于普通高斯分布

GMM 常用于聚类，也就是把每个概率密度分布聚为一类；如果概率密度分布为已知，那就变成参数估计问题

EM 解释 GMM

EM 的核心是 隐变量 和 似然函数

求导结果如下

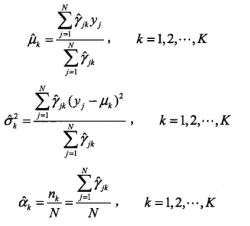
GMM 的 EM 算法

算法流程

Python 实现 GMM

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from scipy.stats import multivariate_normal
plt.style.use('seaborn')

# 生成数据
def generate_X(true_Mu, true_Var):
    ### 生成2000条二维模拟数据，其中400个样本来自N(μ1,var1) ,600个来自N(μ2,var2) ,1000个样本来自N(μ3,var3)
    # 第一簇的数据
    num1, mu1, var1 = 400, true_Mu[0], true_Var[0]
    X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1)
    # 第二簇的数据
    num2, mu2, var2 = 600, true_Mu[1], true_Var[1]
    X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2)
    # 第三簇的数据
    num3, mu3, var3 = 1000, true_Mu[2], true_Var[2]
    X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3)
    # 合并在一起
    X = np.vstack((X1, X2, X3))
    # 显示数据
    plt.figure(figsize=(10, 8))
    plt.axis([-10, 15, -5, 15])
    plt.scatter(X1[:, 0], X1[:, 1], s=5)
    plt.scatter(X2[:, 0], X2[:, 1], s=5)
    plt.scatter(X3[:, 0], X3[:, 1], s=5)
    plt.show()
    return X

# 更新W
def update_W(X, Mu, Var, Pi):
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    W = pdfs / pdfs.sum(axis=1).reshape(-1, 1)
    return W

# 更新pi
def update_Pi(W):
    Pi = W.sum(axis=0) / W.sum()
    return Pi

# 计算log似然函数
def logLH(X, Pi, Mu, Var):
    # 仅计算损失，这步可有可无
    n_points, n_clusters = len(X), len(Pi)
    pdfs = np.zeros(((n_points, n_clusters)))
    for i in range(n_clusters):
        pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i]))
    return np.mean(np.log(pdfs.sum(axis=1)))

# 画出聚类图像
def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None):
    colors = ['b', 'g', 'r']
    n_clusters = len(Mu)
    plt.figure(figsize=(10, 8))
    plt.axis([-10, 15, -5, 15])
    plt.scatter(X[:, 0], X[:, 1], s=5)
    ax = plt.gca()
    for i in range(n_clusters):
        plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'ls': ':'}
        ellipse = Ellipse(Mu[i], 3 * Var[i][0], 3 * Var[i][1], **plot_args)
        ax.add_patch(ellipse)
    if (Mu_true is not None) & (Var_true is not None):
        for i in range(n_clusters):
            plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'alpha': 0.5}
            ellipse = Ellipse(Mu_true[i], 3 * Var_true[i][0], 3 * Var_true[i][1], **plot_args)
            ax.add_patch(ellipse)
    plt.show()

# 更新Mu
def update_Mu(X, W):
    n_clusters = W.shape[1]
    Mu = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Mu[i] = np.average(X, axis=0, weights=W[:, i])
    return Mu

# 更新Var
def update_Var(X, Mu, W):
    n_clusters = W.shape[1]
    Var = np.zeros((n_clusters, 2))
    for i in range(n_clusters):
        Var[i] = np.average((X - Mu[i]) ** 2, axis=0, weights=W[:, i])
    return Var

if __name__ == '__main__':
    # 生成数据
    true_Mu = [[0.5, 0.5], [5.5, 2.5], [1, 7]]
    true_Var = [[1, 3], [2, 2], [6, 2]]
    X = generate_X(true_Mu, true_Var)
    # 初始化
    n_clusters = 3      # 聚类个数
    n_points = len(X)   # 样本数
    Mu = [[0, -1], [6, 0], [0, 9]]  # 3 个期望
    Var = [[1, 1], [1, 1], [1, 1]]  # 3 个方差
    Pi = [1 / n_clusters] * 3
    W = np.ones((n_points, n_clusters)) / n_clusters    # 隐变量，每个样本属于每个分布的概率
    Pi = W.sum(axis=0) / W.sum()    # 每个分布的比率
    # 迭代
    loglh = []
    for i in range(5):
        plot_clusters(X, Mu, Var, true_Mu, true_Var)
        loglh.append(logLH(X, Pi, Mu, Var))
        W = update_W(X, Mu, Var, Pi)
        Pi = update_Pi(W)
        Mu = update_Mu(X, W)
        print('log-likehood:%.3f'%loglh[-1])
        Var = update_Var(X, Mu, W)

参考资料：

https://blog.csdn.net/jinping_shi/article/details/59613054

《统计学习方法》李航