ID3算法(MATLAB)

　　ID3算法是一种贪心算法，用来构造决策树。ID3算法起源于概念学习系统（CLS），以信息熵的下降速度为选取测试属性的标准，即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准，然后继续这个过程，直到生成的决策树能完美分类训练样例。

　　①对当前样本集合，计算所有属性的信息增益；

　　②选择信息增益最大的属性作为测试属性，把测试属性取值相同的样本划为同一个子样本集；

　　③若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处；否则对子样本集递归调用本算法。

---

　　结合餐饮案例实现ID3的具体实施步骤。

　　T餐饮企业作为大型的连锁企业，生产的产品种类比较多，另外涉及的分店所处的位置也不同、数目也比较多。对于企业的高层来讲，了解周末和非周末销量是否有大的区别，以及天气、促销活动等因素是否能够影响门店的销量这些信息至关重要。因此，为了让决策者准确地了解和销量有关的一系列影响因素，需要构建模型来分析天气、是否周末和是否有促销活动对其销量的影响，下面以单个门店来进行分析。

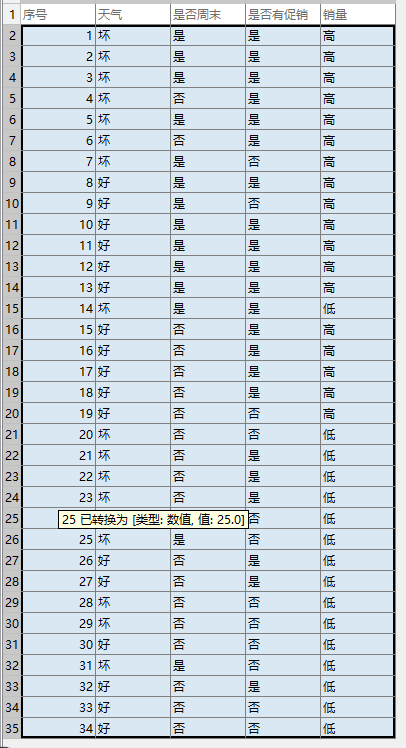
　　①计算总的信息熵，其中数据中总记录数为34，而销售数量为“高”的数据有18，“低”的有16。$$I(18,16)=-\frac{18}{34} \log _{2} \frac{18}{34}-\frac{16}{34} \log _{2} \frac{16}{34}=0.997503$$

　　②计算每个测试属性的信息熵。

　　对于天气属性，其属性值有“好”和“坏”两种。

　　其中天气为“好”的条件下，销售数量为“高”的记录为11，销售数量为“低”的记录为6，可表示为（11，6）；

　　天气为“坏”的条件下，销售数量为“高”的记录为7，销售数量为“低”的记录为10，可表示为（7，10）。

$$\begin{array}{*{20}{l}}
{I(11,6) = - \frac{{11}}{{17}}{{\log }_2}\frac{{11}}{{17}} - \frac{6}{{17}}{{\log }_2}\frac{6}{{17}} = 0.936667}\\
{I(7,10) = - \frac{7}{{17}}{{\log }_2}\frac{7}{{17}} - \frac{{10}}{{17}}{{\log }_2}\frac{{10}}{{17}} = 0.977418}\\
{E\left( {天气} \right) = \frac{{17}}{{34}}I(11,6) + \frac{{17}}{{34}}I(7,10) = 0.957043}
\end{array}$$

　　对于是否周末属性，其属性值有“是”和“否”两种。

　　其中是否周末属性为“是”的条件下，销售数量为“高”的记录为11，销售数量为“低”的记录为3，可表示为（11，3）；

　　是否周末属性为“否”的条件下，销售数量为“高”的记录为7，销售数量为“低”的记录为13，可表示为（7，13）。

$$\begin{array}{*{20}{l}}
{\begin{array}{*{20}{l}}
{I(11,3) = - \frac{{11}}{{14}}{{\log }_2}\frac{{11}}{{14}} - \frac{3}{{14}}{{\log }_2}\frac{3}{{14}} = 0.749595}\\
{I(7,13) = - \frac{7}{{20}}{{\log }_2}\frac{7}{{20}} - \frac{{13}}{{20}}{{\log }_2}\frac{{13}}{{20}} = 0.934068}
\end{array}}\\
{E\left( {是否周末} \right) = \frac{{14}}{{34}}I(11,3) + \frac{{20}}{{34}}I(7,13) = 0.858109}
\end{array}$$

　　对于是否有促销属性，其属性值有“是”和“否”两种。

　　其中是否有促销属性为“是”的条件下，销售数量为“高”的记录为15，销售数量为“低”的记录为7，可表示为（15，7）；

　　其中是否有促销属性为“否”的条件下，销售数量为“高”的记录为3，销售数量为“低”的记录为9，可表示为（3，9）。

$$\begin{array}{*{20}{c}}
{I(15,7) = - \frac{{15}}{{22}}{{\log }_2}\frac{{15}}{{22}} - \frac{7}{{22}}{{\log }_2}\frac{7}{{22}} = 0.902393}\\
{I(3,9) = - \frac{3}{{12}}{{\log }_2}\frac{3}{{12}} - \frac{9}{{12}}{{\log }_2}\frac{9}{{12}} = 0.811278}\\
{E\left( {是否有促销} \right) = \frac{{22}}{{34}}I(15,7) + \frac{{12}}{{34}}I(3,9) = 0.870235}
\end{array}$$

　　③计算天气、是否周末和是否有促销属性的信息增益值。

　　天气：$0.997503-0.957043=0.04046$

　　是否周末：$0.997503-0.858109=0.139394$

　　有无促销属性：$0.997503-0.870235=0.127268$

　　其中，是否周末的信息增益值最大，以其为根节点，其左右分支为“是”与“否”，

　　④依据增益值生成决策树。

　　代码：

%% 使用ID3决策树算法预测销量高低
clear ;
% 参数初始化
inputfile = '../data/sales_data.xls'; % 销量及其他属性数据
%% 数据预处理
disp('正在进行数据预处理...');
[matrix,attributes_label,attributes] =  id3_preprocess(inputfile);
%% 构造ID3决策树，其中id3()为自定义函数
disp('数据预处理完成，正在进行构造树...');
tree = id3(matrix,attributes_label,attributes);
%% 打印并画决策树
[nodeids,nodevalues] = print_tree(tree);
tree_plot(nodeids,nodevalues);
disp('ID3算法构建决策树完成！');

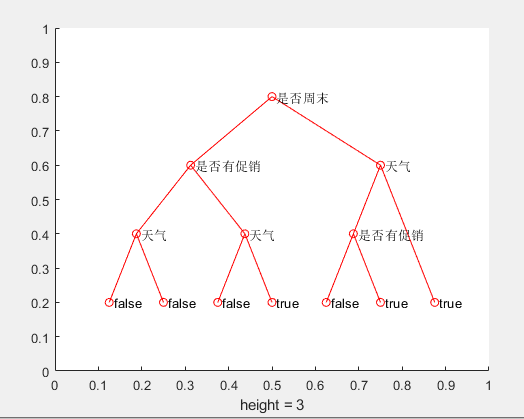
　　依据结果，我们可以得出以下结论：

　　若周末属性为“是”，天气为“好”，则销售数量为“高”；

　　若周末属性为“是”，天气为“坏”，促销属性为“是”，则销售数量为“高”；

　　若周末属性为“是”，天气为“坏”，促销属性为“否”，则销售数量为“低”；

　　若周末属性为“否”，促销属性为“否”，则销售数量为“低”；

　　若周末属性为“否”，促销属性为“是”，天气为“好”，则销售数量为“高”；

　　若周末属性为“否”，促销属性为“是”，天气为“坏”，则销售数量为“低”。

　　由于ID3决策树算法采用了信息增益作为选择测试属性的标准，会偏向于选择取值较多的即所谓的高度分支属性，而这类属性并不一定是最优的属性。同时，ID3决策树算法只能处理离散属性，对于连续型的属性，在分类前需要对其进行离散化。