[51nod1666] 最大值

题面

题解

毒瘤题浪费我大好青春

容易知道, 如果\(l\)和\(r\)位数不一样, 直接选形似\(99..99\)的数, 输出答案即可

\(l\)和\(r\)位数一样的话, 当位数确定的时候, 由于已知\(p\), 所以每一位要跟\(k\)中哪些位相乘已经确定了

设\(f[i]\)为\(k\)中与\(x\)中第\(i\)位相乘的数的和

首先, 每\(lcm(lenx, lenk)\)一个周期, 这个直接暴力算即可

//考虑到x中mod d(lenx与lenk的gcd)同余的数在一个周期内f相等(自己举几个特例, 我不会证)
//故只用枚举mod d的余数即可, 然后模拟选的过程
//假设这个数这一次被选是t时间, p位置, 那么它下一次被选就是(t + lenx)时间, (p + lenx)%lenk位置, 由于我的数组是从1开始, 所以是(p + lenx - 1)%lenk + 1
//然后由于1~lenk中每个数只会被一个i跳到(自己画图, 或者感性理解一下:如果跳到了说明这个周期会更小, 矛盾)
//给每个数标记他被i所跳到的时间(这个等会会用到) 也就是pos, 再给每个位置标记上他被i跳到时累加的值, 也就是sum
for(int i = 0; i < d; i++)
{
	int num = 0, poss = 1, j = i + 1;
	do
	{
		num += k[j];
		pos[j] = poss;
		sum[j] = num;
		++poss;
		j = ((j + l[0] - 1) % k[0] + k[0]) % k[0] + 1;
	}
	while(j != i + 1);
	g[i] = num;
}

这样就可以计算出整个周期的\(f[]\)的值, 然后我们看怎么计算不是整周期的\(f[]\)的值

由于每个位置跳了多少次是可以算出来的, 所以我们可以算出来它最后在哪一个位置

然后用终点的\(sum\)减去起点的\(sum\)即可

但是有一个细节, 就是当终点的\(pos\)小于等于起点的\(pos\)时, 它要加上一个\(g[i \% d]\), 根据图理解一下吧, 我讲不清

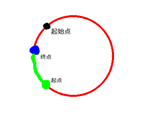
这个图太小了吧...

算了, 蓝色点是终点, 绿色点是起点, 可以知道起点到终点是那条红色路径, 然后你如果用终点的\(sum\)减去起点的\(sum\)就是负的绿色的那条, 加上一个\(g[i \% d]\)就是那条红色的了

最后讲一下统计答案

考虑贪心

对于一个数x, 它的前\(i\)位跟\(r\)一样, 第\(i + 1\)位小于\(r[i + 1]\), 后面的都是9, 这样必定是最优的, 从后往前不断更改这个\(i + 1\)的位置即可

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
#define itn int
#define reaD read
#define N 100005
#define int long long
using namespace std;

int l[N], r[N], k[N], pos[N];
long long p, res1, res2, ans, g[N], sum[N], f[N];

template < typename T >
inline T read()
{
	T x = 0, w = 1; char c = getchar();
	while(c < '0' || c > '9') { if (c == '-') w = -1; c = getchar(); }
	while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
	return x * w;
}

int gcd(int m, int n) { return !n ? m : gcd(n, m % n); }

signed main()
{
	char c = getchar();
	while(c < '0' || c > '9') c = getchar();
	while(c >= '0' && c <= '9') l[++l[0]] = c - '0', c = getchar();
	while(c < '0' || c > '9') c = getchar();
	while(c >= '0' && c <= '9') r[++r[0]] = c - '0', c = getchar();
	while(c < '0' || c > '9') c = getchar();
	while(c >= '0' && c <= '9') k[++k[0]] = c - '0', c = getchar();
	p = read <long long> ();
	if(l[0] < r[0])
	{
		int r = p % k[0], q = p / k[0];
		for(int i = 1; i <= k[0]; i++)
			ans += k[i] * (q + (i <= r)) * 9;
		printf("%lld\n", ans); return 0;
	}
	int d = gcd(l[0], k[0]);
	for(int i = 0; i < d; i++)
	{
		int num = 0, poss = 1, j = i + 1;
		do
		{
			num += k[j];
			pos[j] = poss;
			sum[j] = num;
			++poss;
			j = ((j + l[0] - 1) % k[0] + k[0]) % k[0] + 1;
		}
		while(j != i + 1);
		g[i] = num;
	}
	int q = p / (l[0] * k[0] / d), x = p % (l[0] * k[0] / d), w = x / l[0], y = x % l[0];
	for(int i = 1; i <= l[0]; i++)
	{
		f[i] = g[((i - 1) % d + d) % d] * q;
		int cnt = w + (i <= y);
		if(!cnt) continue;
		int lst = ((i - l[0] - 1) % k[0] + k[0]) % k[0] + 1, nxt = ((i + (cnt - 1) * l[0] - 1) % k[0] + k[0]) % k[0] + 1;
		f[i] += sum[nxt] - sum[lst] + (pos[nxt] <= pos[lst] ? g[((i - 1) % d + d) % d] : 0);
	}
	int top = 1;
	while(top <= l[0] && l[top] == r[top]) top++;
	for(int i = 1; i <= l[0]; i++)
		res1 += r[i] * f[i];
	ans = res1; res1 -= f[l[0]];
	for(int i = l[0]; i >= top + 1; i--)
	{
		res1 += (10 - r[i]) * f[i];
		res1 -= f[i - 1];
		ans = max(ans, res1);
	}
	printf("%lld\n", ans);
	return 0;
}