VLC-Qt 入门指南

 

关于 VLC-Qt

VLC-Qt：一个结合了 Qt 应用程序和 libVLC 的免费开源库。它包含了用于媒体播放的核心类，以及用于更快速地进行媒体播放器开发的一些 GUI 类。

• 官网地址：https://vlc-qt.tano.si/
• Github 地址：https://github.com/vlc-qt
• 示例地址：https://github.com/vlc-qt/examples

由于 VLC-Qt 集成了整个 libVLC，因此具备 libVLC 的所有特性，例如：libVLC 实例和 player、单个文件和列表播放、音频和视频控制、元数据管理。

如果想快速创建一个功能齐全的跨平台媒体播放器，这个库非常合适！

| 版权声明：一去、二三里，未经博主允许不得转载。

主要组成

VLC-Qt 主要包含三大部分：

• 核心库

连接到 libVLC 并控制播放。核心类使我们能够完全控制 libVLC 及其所有特性，它能让我们完全控制播放。Widgets 和 QML 类只是简化了与核心的通信，但是没有引入任何新特性。

整个 libVLC 库被完全封装到了 C++/Qt 中，它仍然可以同时支持多个实例和/或播放器。还可以访问 libVLC 对象，以获得所有包装的功能。

• Widgets 库

媒体播放器通常需要一个 UI，Widgets 部分包含了几个简单的、预先制作的窗口部件 ，可以将其用作基类：video widget、seek widget、volume slider、audio 和 video controllers。

• QML 库

VLC-Qt 还包含了 QML 部分，它提供了使用 OpenGL 的简单视频播放。

编译安装

要使用 VLC-Qt，首先需要下载它。可以自己编译，也可以使用官网上编译好的版本。

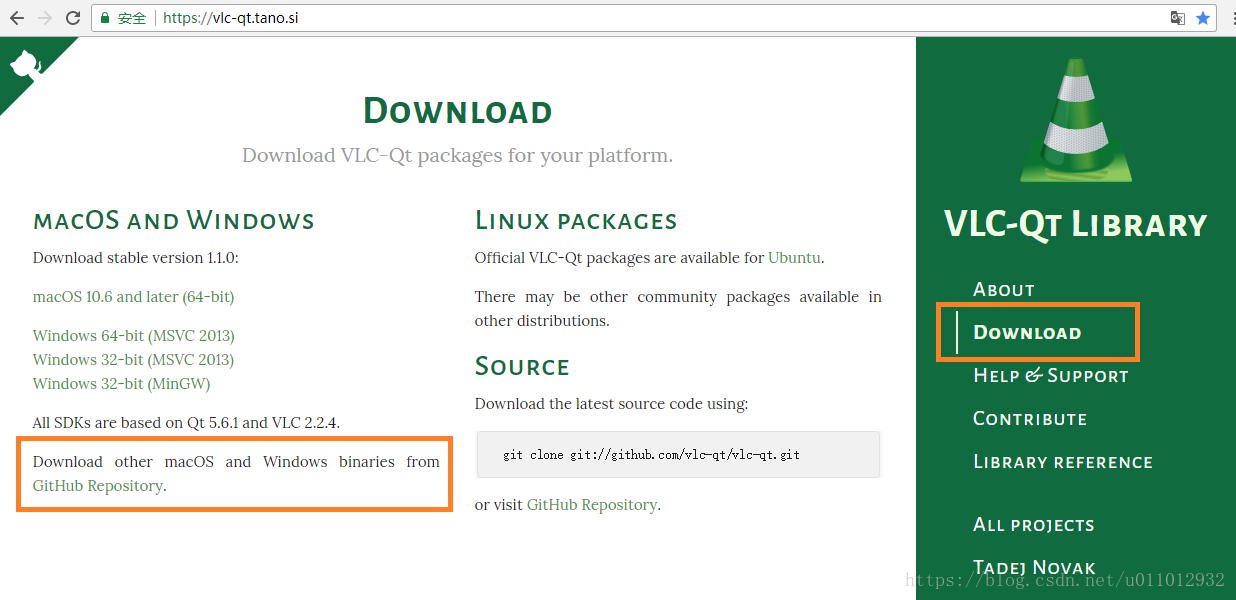
进入官网，选择右边导航中的【Download】，然后可以选择自己需要的版本:

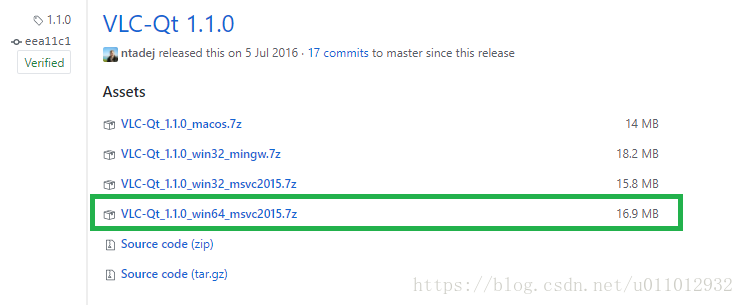
由于我的环境是 MSVC 2015，这里没有对应的版本，所以需要点击“GitHub Repository”选择其他版本：

下载 VLC-Qt_1.1.0_win64_msvc2015.7z，然后解压到 VLC-Qt-Install（下面会用到），它里面有三个子文件夹：

• include：包含了所需的头文件
• lib：包含所需的 lib 文件
• bin：包含了所需的 dll 文件（动态库及插件）

基本使用

VLC-Qt 的使用很简单，可以打开最上面的示例地址，来学习如何使用。

下载示例，然后打开 simple-player.pro，并将 src.pro 中的 VLC-Qt 相关设置改为自己的路径：

# VLC-Qt 安装目录
VLC_INSTALL_PATH = $$PWD/../../../VLC-Qt-Install

# VLC-Qt 相关库
CONFIG(debug, debug|release) {
    LIBS += -L$$VLC_INSTALL_PATH/lib -lVLCQtCored -lVLCQtWidgetsd
} else {
    LIBS += -L$$VLC_INSTALL_PATH/lib -lVLCQtCore -lVLCQtWidgets
}

# VLC-Qt 相关头文件目录
INCLUDEPATH += $$VLC_INSTALL_PATH/include

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12

注意： 这里的 VLC_INSTALL_PATH 为 VLC-Qt 解压缩之后的路径，除了使用相对路径之外，也可使用绝对路径。

然后，执行qmake -> 构建，运行程序。

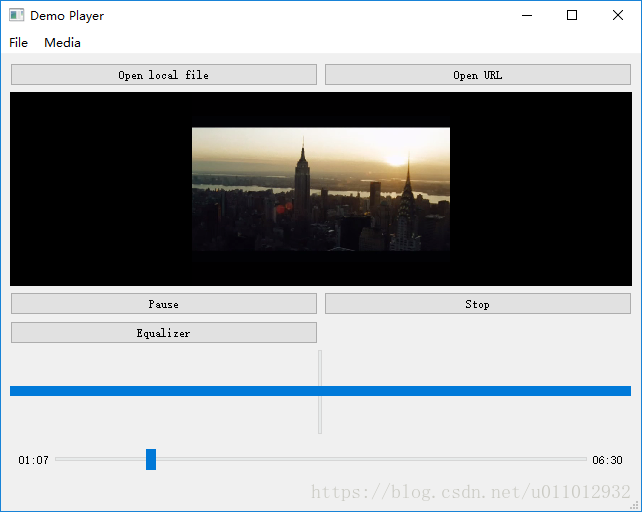
播放本地视频：

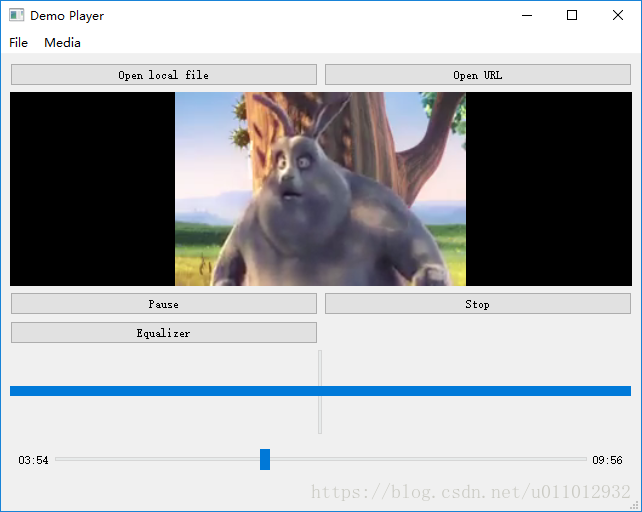
播放 RTSP 流：

如果找不到合适的 RTSP 地址，可以使用 RTSP_Video_Streaming_URLs 里面的地址进行测试。