DSB的数字正交解调

1.DSB调制过程

​ DSB信号是一种双边带调幅调制信号，又叫双边带调幅，通过改变载波的振幅来实现基带数据的传输。

其函数表达式如下：

\[s(t) = m(t)*cos(2\pi ft + \varphi)
\]

其中：

m(t):表示基带信号。

\(cos(2\pi ft + \varphi )\):表示载波信号。

2.DSB的数字正交解调

​ 以下介绍的正交解调法将消除频差或者相差带来的误差，增加其解码正确率。

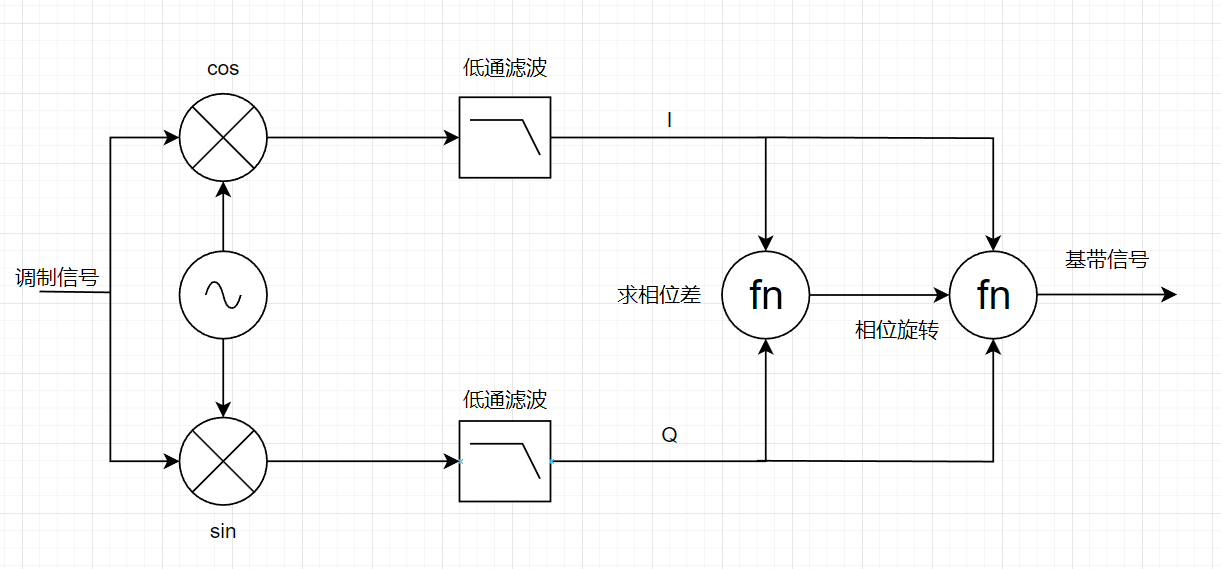
通过正交的方式即可解调出基带信号，其数学推导如下：

​ 假设基带信号为\(m(t)\)，调制的载波频率为\(f_1\)，解调的载波频率为\(f_2\)，相位为\(\varphi\),LPF为低通滤波器，则：

I路：

\[I(t) = LPF(s(t)*cos(2\pi f_2t + \varphi)) = LPF(m(t)*cos(2\pi f_1t) *cos(2\pi f_2t + \varphi))
\]

根据三角函数公式：

\[\begin{split}
I(t) &= LPF(m(t)*cos(2\pi f_1t) *cos(2\pi f_2t + \varphi))\\
&= LPF(\frac{1}{2}m(t)*[cos(2\pi (f_1 + f_2)t+\varphi) + cos(2\pi (f_1 - f_2 )+ \varphi)]) \\
&= \frac{1}{2}m(t)*cos(2\pi (f_1 - f_2 )+ \varphi)) \\
\end{split}
\]

同理：Q路：

\[\begin{split}
Q(t) &= LPF(m(t)*cos(2\pi f_1t) *sin(2\pi f_2t + \varphi))\\
&= LPF(\frac{1}{2}m(t)*[cos(2\pi (f_1 + f_2)t+\varphi) - sin(2\pi (f_1 - f_2 )+ \varphi)]) \\
&= -\frac{1}{2}m(t)*sin(2\pi (f_1 - f_2 )+ \varphi)) \\
\end{split}
\]

对于解调系统来说：当\(f_1=f_2，\varphi=0\)时，

\[\begin{split}
& I(t) = \frac{1}{2}m(t) \\
& Q(t) = 0 \\
\end{split}
\]

​ 这时，就可以完美还原基带信号，但是此方法严格要求发射载波与接收载波频率相同，而且相位保持一致，相位误差与载波频率误差将严格限制解调系统的精确度，所以一下将使用其他解调方法来规避，相位差与频率差带来的解调误差。

​ 为了计算方便假设：

\[K=2\pi (f_1 - f_2 )+ \varphi
\]

则：

\[\begin{split}
& I(t) = \frac{1}{2}m(t)*cos(K) \\
& Q(t) = -\frac{1}{2}m(t)*sin(K)
\end{split}
\]

根据三角函数公式：

\[K = arctan(\frac{-Q(t)}{I(t)})
\]

注：\(arctan\)函数有作用域\((-\pi/2\space\space\space\space\pi/2)\)要求，所以将使用其他函数替代。

\[\begin{split}
& I(t) = \frac{1}{2}m(t)*cos(arctan(\frac{-Q(t)}{I(t)})) \\
& Q(t) = -\frac{1}{2}m(t)*sin(arctan(\frac{-Q(t)}{I(t)}))
\end{split}
\]

以下将是重要的地方：

向量旋转，将一个向量\((cos(\theta_1),sin(\theta_2))\),逆时针旋转\(\theta_2\),旋转后的坐标为\((cos(\theta_1-\theta_2),sin(\theta_2-\theta_2))\)。将I和Q看着一个向量，将其逆时针旋转\(arctan(\frac{-Q(t)}{I(t)})\),那么：

\[\begin{split}
& I'(t) = \frac{1}{2}m(t)*cos(arctan(\frac{-Q(t)}{I(t)}) - arctan(\frac{-Q(t)}{I(t)})) =\frac{1}{2}m(t)\\
& Q'(t) = -\frac{1}{2}m(t)*sin(arctan(\frac{-Q(t)}{I(t)}) - arctan(\frac{-Q(t)}{I(t)})) = 0
\end{split}
\]

这样就消除了相位差和频率差带来的误差，\(I'(t)\)就是我们解调的结果。其结果与频率差与相位差无关。

3.MATLAB解调

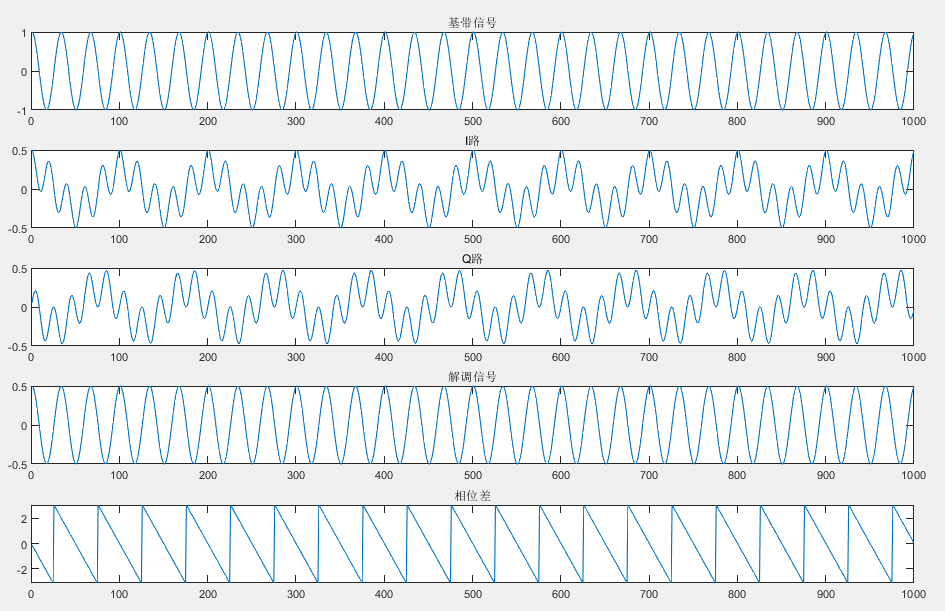
以下只展示解调过程的仿真，不展示下变频，滤波等操作：

close all;
%% 系数
figure
time = 5;

fs = 100E6; % 采样率 (Hz)
len = 1E3; % 信号序列点数
f_base = 3E6;%基带信号频率
f_carr_1 = 40E6;%调制载波频率
f_carr_2 = 42E6;%解调载波频率
fi = 0.1;%解调载波初始相位
t = 0:1/fs:(len-1)/fs; % 时间向量
mt = cos(2*pi*f_base*t);
I = mt.*cos(2*pi*(f_carr_1-f_carr_2)*t-fi)/2;
Q = -mt.*sin(2*pi*(f_carr_1-f_carr_2)*t-fi)/2;

%% 向量旋转
theta = atan2(Q./(-mt),I./(mt));
It = I.*cos(theta) - Q.*sin(theta);
Qt = Q.*cos(theta) + I.*sin(theta);

subplot(time,1,1);
plot(mt);
title('基带信号');

subplot(time,1,2);
plot(I);
title('I路');

subplot(time,1,3);
plot(Q);
title('Q路');

subplot(time,1,4);
plot(It);
title('解调信号');

subplot(time,1,5);
plot(theta);
title('相位差');

结果：

5.FPGA解调

有空补齐FPGA解调部分代码。