【2020.11.19提高组模拟】倍数区间interval 题解

【2020.11.19提高组模拟】倍数区间interval 题解

题目描述

定义在序列\(a_1,a_2,\dots,a_n\)上的合法区间\([L,R]\)为满足\(\exists k\in [L,R],\forall i\in [L,R],a_k\mid a_i\)。

即存在一个数\(a_k\)，满足区间内所有的数都是\(a_k\)的倍数。

求最长的合法区间长度并输出这些区间的左端点。

Solution

又是区间问题。

首先找到几个结论：

1.\(a_k\)一定是这个区间内最小的数。

2.\(a_k\mid 区间gcd\)。

第一个很显然，倍数当然要大于或等于自己的。

第二个也很显然，\(区间gcd\)就是这个区间内所有数的因数的交集。

那么我们可以用ST表预处理出区间\(gcd\)，然后对于每个数当作它是那个\(a_k\)，左右各自二分出最远的合法区间即可。

复杂度\(O(n\log^2 n)\)。

Code-ST

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#define debug printf("Now is %d\n",__LINE__);
using namespace std;

template<class T>inline void read(T&x)
{
    char ch=getchar();
    int fu;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') fu=-1,ch=getchar();
    x=ch-'0';ch=getchar();
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    x*=fu;
}
inline int read()
{
	int x=0,fu=1;
    char ch=getchar();
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') fu=-1,ch=getchar();
    x=ch-'0';ch=getchar();
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
    int g=0;
    if(x<0) x=-x,putchar('-');
    do{G[++g]=x%10;x/=10;}while(x);
    for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar(' ');
}
int n;
int lg[1000010];
int gcd[1000010][24];
int GCD(int a,int b)
{
//	cout<<"gcd a="<<a<<" b="<<b<<" ";
	int t;
	while(b)
	{
		t=b;
		b=a%b;
		a=t;
	}
//	cout<<"gcd="<<a<<endl;
	return a;
}
void pre()
{
	lg[1]=0;
	for(re int i=2;i<1000010;i++) lg[i]=lg[i>>1]+1;
	for(re int j=1;j<=22;j++)
	{
		for(int i=1;i+(1<<j)-1<=n;i++)
		{
			gcd[i][j]=GCD(gcd[i][j-1],gcd[i+(1<<(j-1))][j-1]);
		}
	}
}
int ask(int l,int r)
{
	return GCD(gcd[l][lg[r-l+1]],gcd[r-(1<<lg[r-l+1])+1][lg[r-l+1]]);
}
int maxans;
int ans[500010];
int sze;
//out:sze-maxans\nans
int main()
{
	freopen("interval.in","r",stdin);
	freopen("interval.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++) gcd[i][0]=read();
	pre();
	for(int k=1,L,R,l,r,mid;k<=n;k++)
	{
		l=1,r=k;
		while(l!=r)
		{
			mid=(l+r)/2;
			if(ask(mid,k)%gcd[k][0]==0) r=mid;
			else l=mid+1;
		}
		L=l;
		l=k,r=n;
		while(l<r)
		{
			mid=(l+r+1)/2;
			if(ask(k,mid)%gcd[k][0]==0) l=mid;
			else r=mid-1;
		}
		R=r;
//		cout<<L<<" "<<R<<endl;
		if(R-L>maxans) maxans=R-L,sze=0;
		if(R-L==maxans&&ans[sze]!=L) ans[++sze]=L;
	}
	printf("%d %d\n",sze,maxans);
	for(int i=1;i<=sze;i++) write(ans[i]);
	return 0;
}

upd

但是其实有一种\(O(n\log n)\)的做法！

我在考试的时候打暴力时打的就是这样的优化，我觉得它的时间过不去，但是其实比上面的算法还要暴力，复杂度还要小！

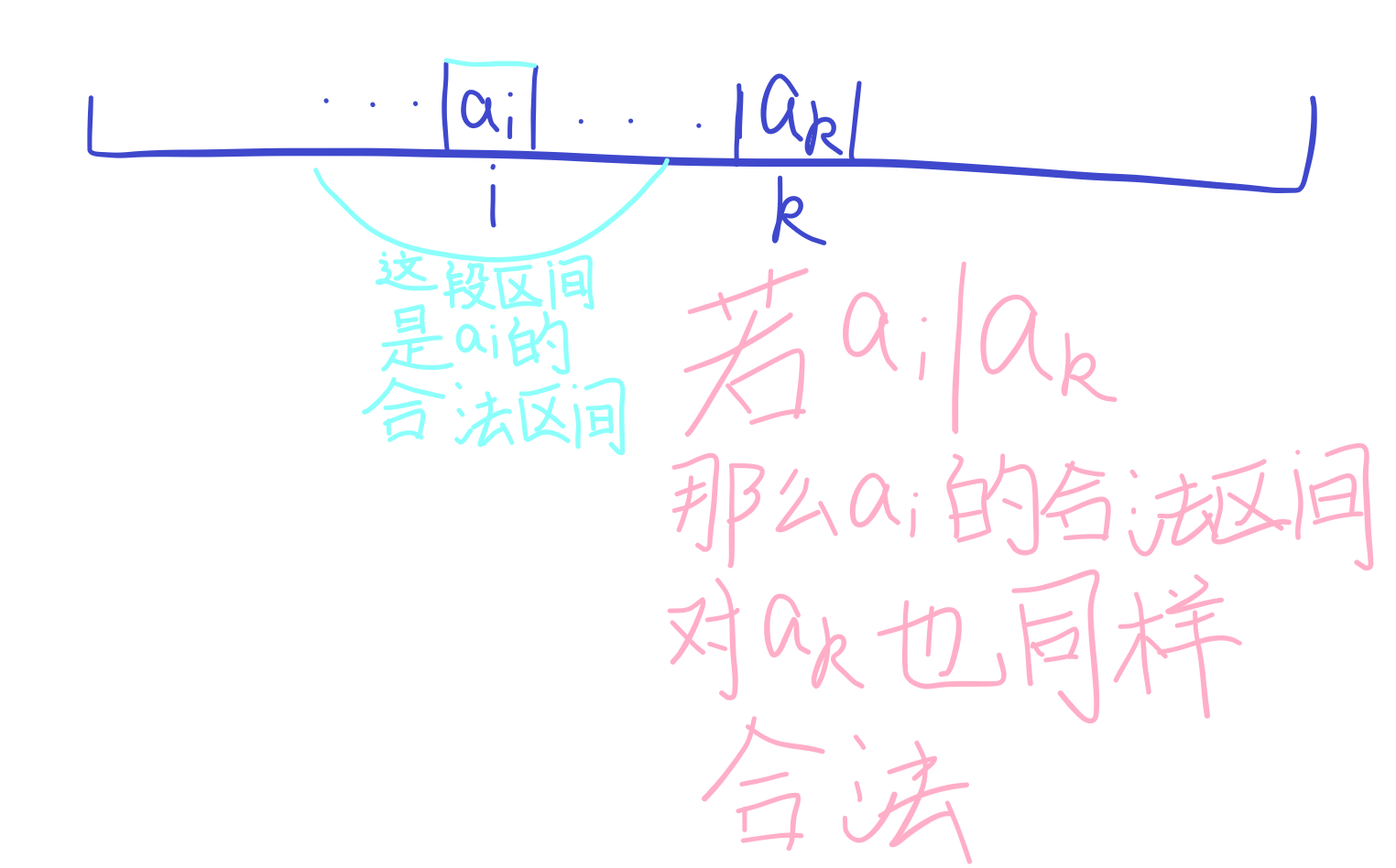
利用第一个性质——自己的倍数的倍数也是自己的倍数。

那么每次对一个数扩展完之后记录一下区间的左右端点。

之后对后面的数\(a_k\)扩展时，若发现有一个\(a_k\mid a_i(i<k)\)，那么当前的区间的左端点可以直接跳转到\(a_i\)的合法区间左端点。同理，右端点也可以跳。

Code

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#define debug printf("Now is %d\n",__LINE__);
using namespace std;

template<class T>inline void read(T&x)
{
    char ch=getchar();
    int fu;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') fu=-1,ch=getchar();
    x=ch-'0';ch=getchar();
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    x*=fu;
}
inline int read()
{
	int x=0,fu=1;
    char ch=getchar();
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') fu=-1,ch=getchar();
    x=ch-'0';ch=getchar();
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
    int g=0;
    if(x<0) x=-x,putchar('-');
    do{G[++g]=x%10;x/=10;}while(x);
    for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar(' ');
}
int n;
int a[500010];
int kmp[500010],gkd[500010];
int ans;
int L[500010];
int sze;
//out:size-ans\nL
int main()
{
	freopen("interval.in","r",stdin);
	freopen("interval.out","w",stdout);
	n=read();
	for(re int i=1;i<=n;i++) a[i]=read(),kmp[i]=i;
	for(re int i=1,l,r;i<=n;i++)
	{
//		debug cout<<"i="<<i<<endl;
		for(l=i-1,r=i+1;l>0;l--)
		{
//			debug
			if(a[l]<a[i]||a[l]%a[i]) break;
//			debug
//			cout<<"l="<<l<<endl;
			l=kmp[l];
			r=max(r,gkd[l]);
		}
		l++;
		kmp[i]=l;
		for(;r<=n;r++)
		{
//			debug
			if(a[r]<a[i]||a[r]%a[i]) break;
//			debug
		}
		r--;
		gkd[i]=r;
		if(r-l>ans)
		{
			ans=r-l;
			sze=0;
		}
		if(r-l==ans&&L[sze]!=l)
		{
			L[++sze]=l;
		}
	}
	printf("%d %d\n",sze,ans);
	for(int i=1;i<=sze;i++)
	{
		write(L[i]);
	}
	return 0;
}

小结

注意最后的结果要判重哦！否则\(score-=30pts\)！