CRC和LFSR

先说下LFSR，中文叫线性反馈移位寄存器，英文的全称是了linear feedback shift register，这个其实是由SR—>FSR—>LFSR逐步发展出来的，SR也就是移位寄存器，这个我们都很熟悉，串并转换里经常用，网上找个图：



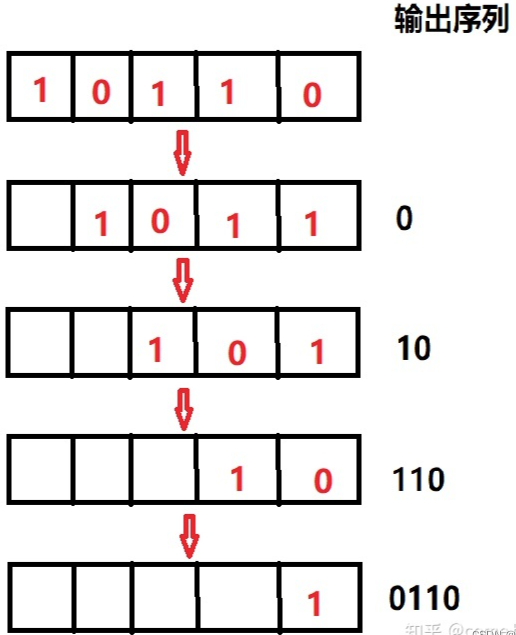
也就是数据挨个从左到右（从右到左）的移出，右边移出一位左边就空出一位，空出的这一位大部分情况下默认补0，如果这一位我们通过某个函数来计算，这个函数的输入就是寄存器组中已有的这些数，函数的输出填到左边空出的这一位，通过这种方式我们就进一步得到了反馈寄存器，也就是FSR，它可以源源不断的进行输出，贴个图：



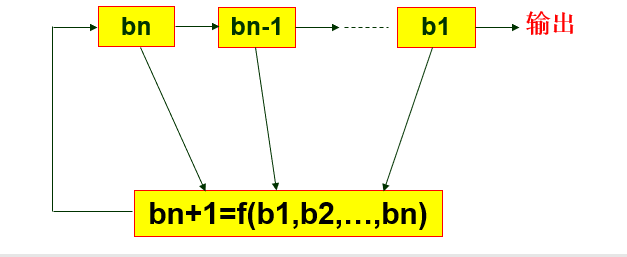
再进一步，如果这个反馈函数，是一个线性的函数呢？这里略微补充下线性函数的定义，就是满足f（ax+by）=af（x）+bf（y）这样的函数，典型的就是f=ax+b，而LFSR的反馈函数定义如下：



其中的加法是异或（XOR），乘法是与（AND），Ifsr的反馈函数也满足：



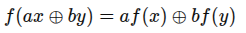
所以LFSR是一个线性反馈移位寄存器，上面式子：\(s_{n+k}=c_1 s_{n+k-1} \oplus c_2 s_{n+k-2} \oplus \cdots \oplus c_k s_n\)，\(c_1\) \(c_2\)...我们称为系数，值为0或者为1，为1就是表示该位置的值参与计算，参与计算的位也叫抽头，相应的为0就是不参与计算。而寄存器里最开始的的所有值我们称为初始值，也叫种子，基于抽头，我们可以得出一个叫反馈多项式的东西，它就是根据抽头所在的寄存器位置，给多项式定义幂次，举个例子：



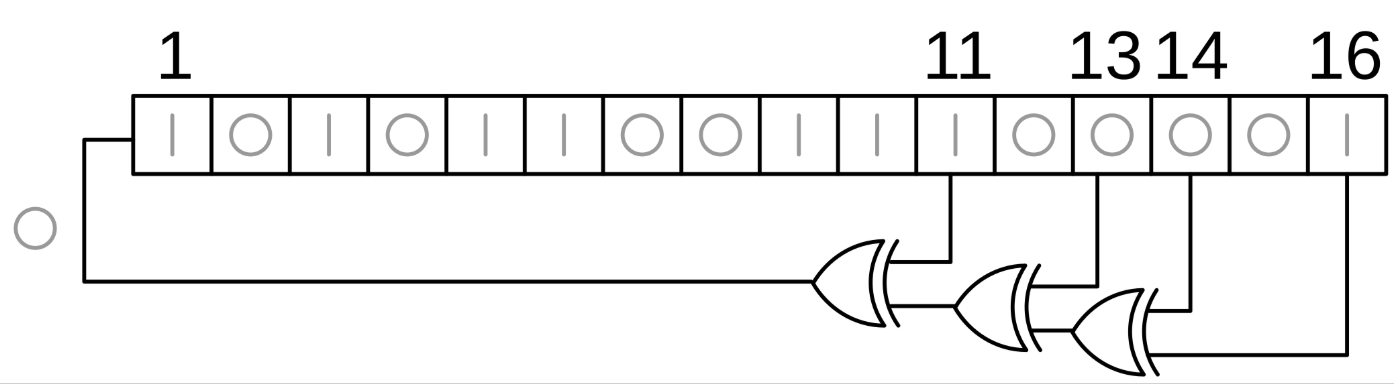
上图的LFSR级数为16，抽头位置为16 14 13 11，注意图里的位置1并不表示抽头，而是说这里是一个输入，是之前那些值经过反馈函数给返回来的，因为这是反馈移位寄存器，这一位必须要有，所以必须为1，你也可以理解为X^0,也就是1，数学上表达就是：

1*X^16 + 0*X^15 + 1*X^14 + 1*X^13 + 0*X^12 + 1*X^11 + 0*X^10 + 0*X^9 + 0*X^8 + 0*X^7 + 0*X^6 + 0*X^5 + 0*X^4 + 0*X^3 + 0*X^2 + 0*X^1 + X^0

等价于：

X^16 + X^14 + X^13 + X^11 + 1

对应的2进制就是：

10110100000000001

一共17位，但是LFSR的表达式最高位都为1，默认省略不写，也就是：

0110100000000001

对应的16进制值是0x6801

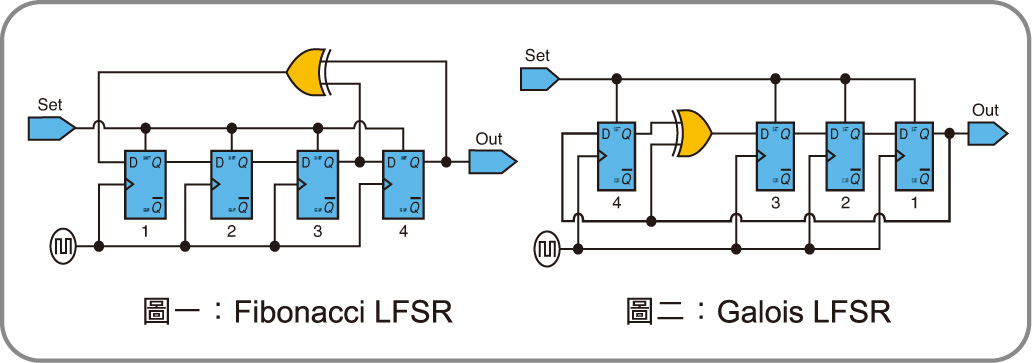
LFSR的基础介绍的差不多了，我们再说LFSR常见的两种形式：

• Fibonacci LFSRs 斐波那契型
• Galois LFSRs 伽罗瓦型
  
  Fibonacci LFSRs就是多到1，就是多个抽头位置的值一起异或，生成的结果给到左边空出的那一位，而Galois LFSRs则是抽头位置前一级寄存器的值和输出寄存器的值异或后给到抽头位置的寄存器，贴张图：
  
  

好，介绍到这里，我们就开始说CRC，CRC, 全称Cyclic Redundancy Check，中文循环冗余校验，它的原理其实是模2除法的运算，模2除法就是异或运算，要校验的原始数据就是被除数，除数就是一组选定的特殊数据，也就是多项式的2进制表达式，它俩除下来的余数补到原始数据的后面，而接收端收到数据后，会再去执行模2的除法，因为余数已经补上去了，所以接收方计算时，应该是正好能整除的，也就是余数为0。举个例子吧：



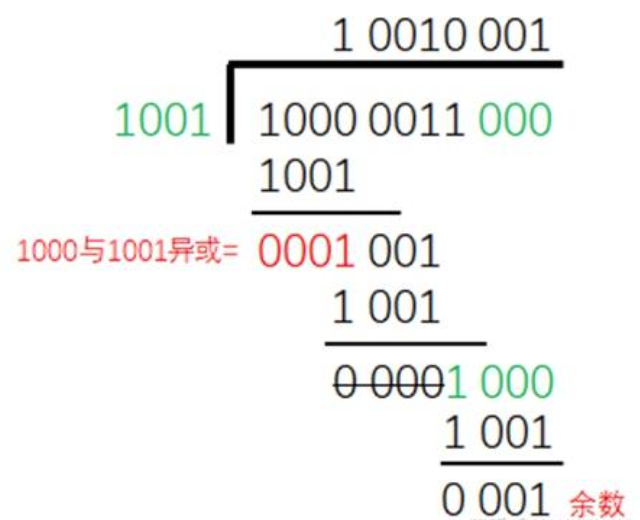
图里被除数是10000011，除数是1001，多项式就是X^3+1,0x01(最高位默认为1不写)，图里我们看到它计算的时候是在原始数据10000011后面补了3个0，因为在多项式除法里，余数的最高次幂一定是小于除数最高次项，除数最高次为3，也就是4位，那余数最高次为2，也就是3位，所以是预留3位。换个角度想，补3个0，也就是把原始数据左移了3位，其实就是给后面把余数补上去时候，预先留的位置，虽然不知道余数是多少，但是余数的位数，一定数小于除数的位数。好，现在我们把余数补上去，再算一遍：



余数正好是0，证明数据没有问题。我们可以找个工具验证一下：



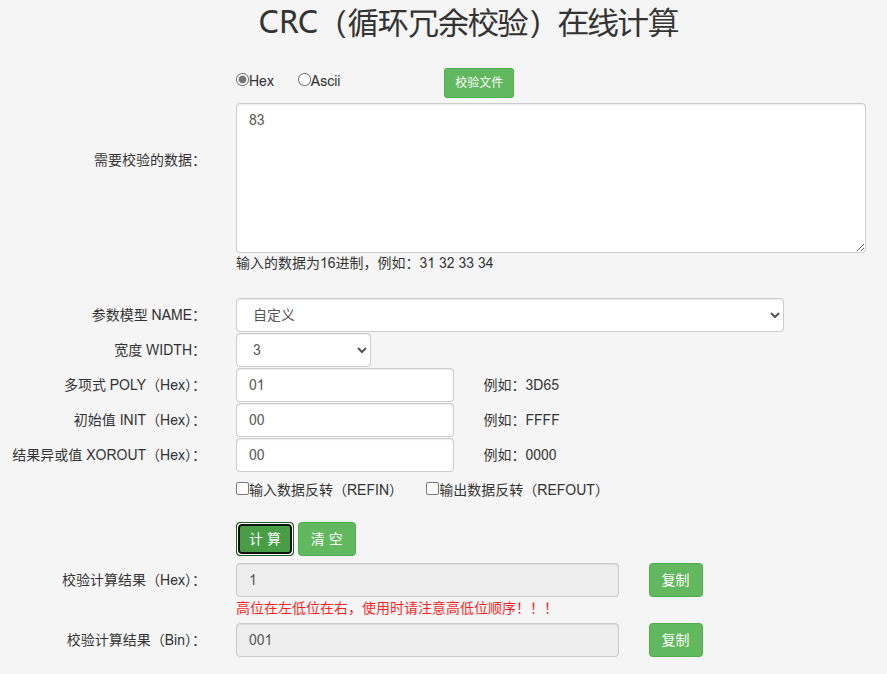
结果和我们的一致，没有问题。

好了说了这么多，那CRC这种模2运算，和LFSR有啥关系？到目前为止，我们看到了LFSR是异或运算，CRC的模2除法也是异或运算，我们回看上面CRC计算步骤时，会发现，除的过程其实就是被除数左移，和除数异或的过程，具体逻辑是，判断被除数MSB(最高位)是否为1，如果是的话就进行异或操作，然后余数左移1位，再在右边补上和原始被除数相对应的位的值，形成新的被除数，如果MSB为0，则直接左移，同样补上原始被除数相对应的位的值，一直到被除数MSB为1为止，前面我们说过多项式最高位一定是1，所以每当我们进行异或操作时，余数的高位一定是0，所以不管怎么说，我们都会左移，也就是每次余数肯定会左移一位，文字描述很繁琐，还是贴个图：



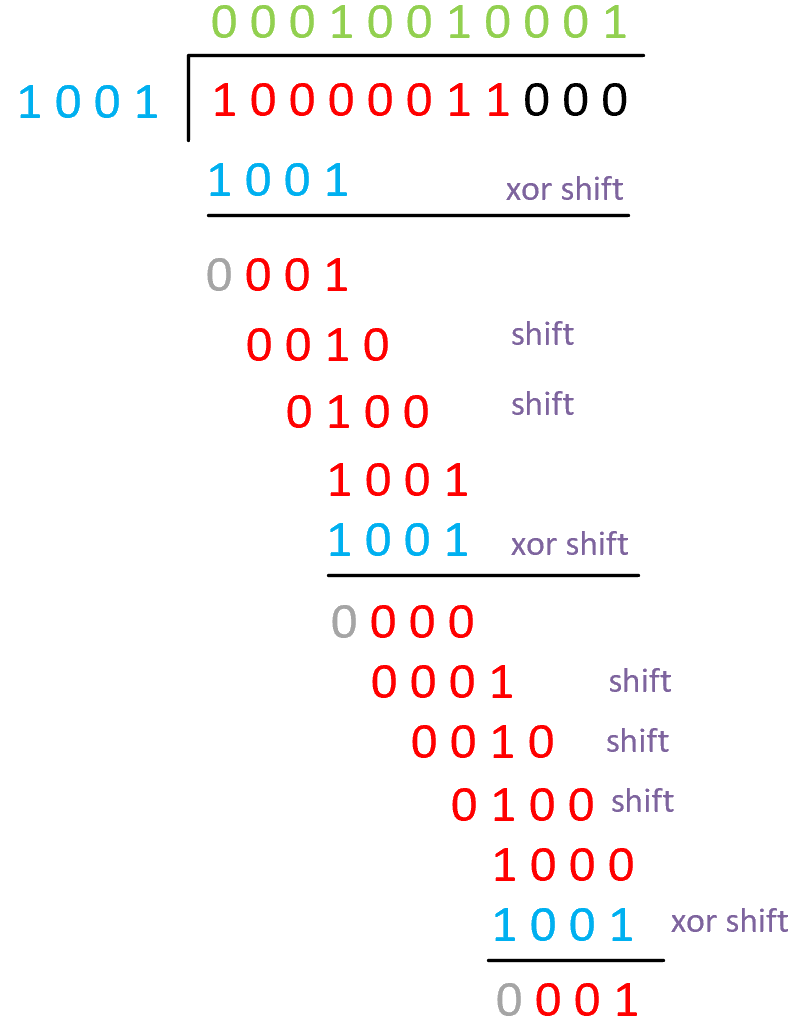
文字描述下上图的计算过程，首先，被除数开始是1000_0011，右边补3个0预留余数位置，除数是1001，当前被除数MSB为1，在第四位商1进行异或，得到余数0001，也就是新的被除数，新的被除数MSB为0(一定为0)，继续补数。补上面原始被除数相对应位的数，也就是0，同时左移1位，把为0的MSB给丢掉，这时新的被除数为0010，MSB还不是1，继续操作上一步，得新的被除数0100，还是不行，继续，得1001，这下满足了，就进行异或操作，重复以上部分，最终得余数001，也就是我们想要的结果。这个运算过程，是怎么转化成lfsr的呢，我先贴个图出来：



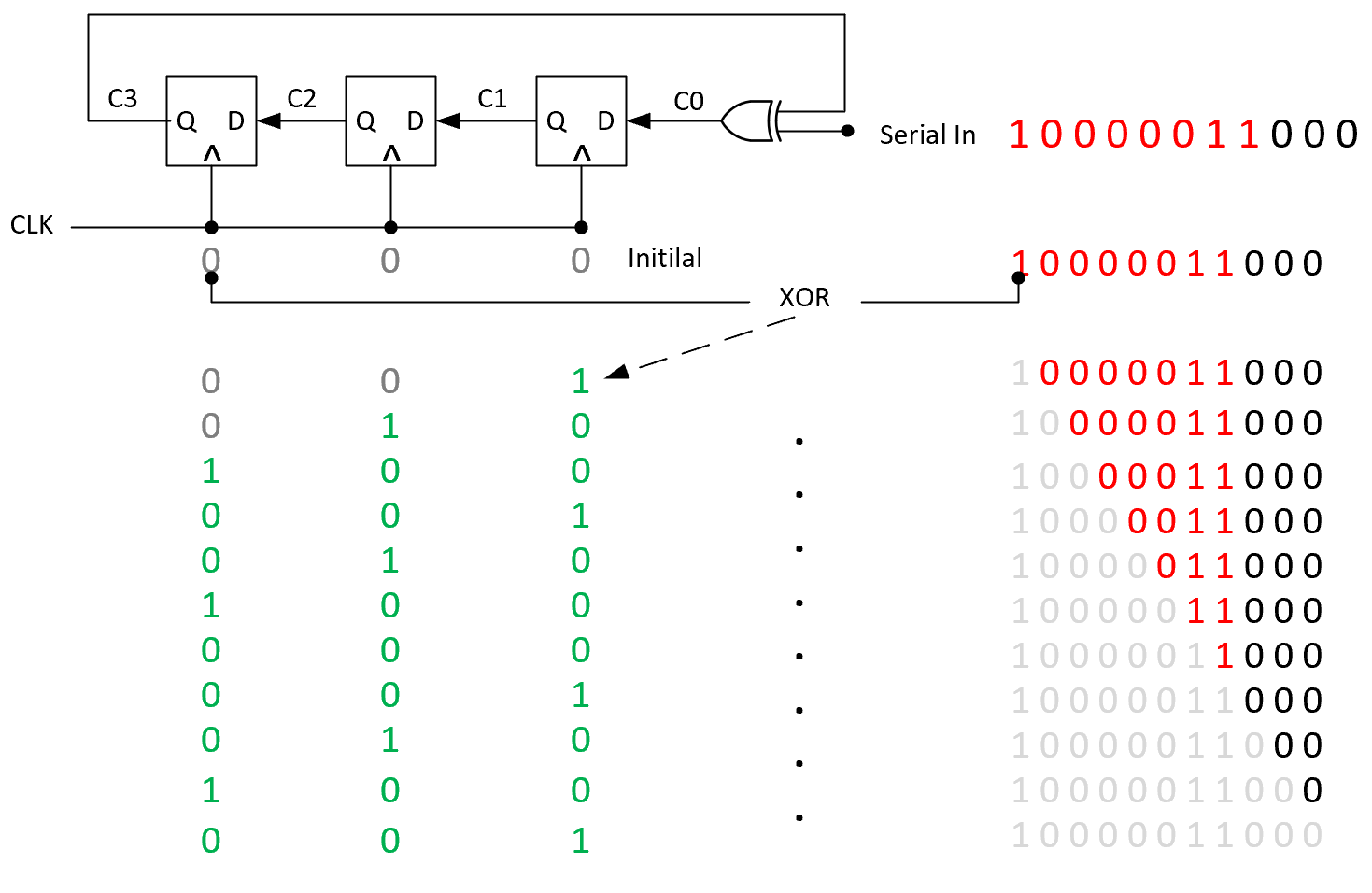
这个lfsr图，c3 c2 c1 c0其实就是上面我们说lfsr线性函数里的抽头，对应的就是除数1001，最高位寄存器其实就是MSB,当MSB为1时，就进行异或并把值移入LSB寄存器，否则就只是左移没有异或，最终当输入都移完了，寄存里最终的值其实就是余数，也就是我们要的CRC，我们发现其实lfsr寄存器状态并不是每一步和模2除法的余数都能对上，因为模2除法是一次异或4位，lfsr是流水1bit操作的，这里有个很核心的其实我们没有讲，就是为什么crc转换出来的lfsr是张这样的，为什么这样就正好是最后的余数，这个涉及到M位多项式除法运算的计算推导，实话说我自己还没弄懂推导出来，实在是笨和懒了。。。下次再补上。最后再贴几个代码吧：

以下我根据10G eth里的64b66b多项式写的代码，我详细的列出了运算的步骤：

/***************************************************************************
    Fibonacci style (example for 64b66b scrambler, 0x8000000001)

    DIN (LSB first)
        |
        V
       (+)<---------------------------(+)<-----------------------------.
        |                              ^                               |
        |  .----.  .----.       .----. |  .----.       .----.  .----.  |
        +->|  0 |->|  1 |->...->| 38 |-+->| 39 |->...->| 56 |->| 57 |--'
        |  '----'  '----'       '----'    '----'       '----'  '----'
        V
    DOUT

                                                                 bit width 64            58
                                                                 value[pos]
    data_out[0] = data_in[0] ^ state[57] ^ state[38]     mask   000.......001[0]    1[57]0000....1[38].....0
    data_out[1] = data_in[1] ^ state[56] ^ state[37]            000......01[1]0    01[56]0000....1[37]....0
    data_out[2] = data_in[2] ^ state[55] ^ state[36]            000......1[2]00    001[55]0000....1[36]...0

    DIN (LSB first)
        |
        V
       (+)<---------------------------(+)<-----------------------------.
        |                              ^                               |
        |  .----.  .----.       .----. |  .----.       .----.  .----.  |
        +->| 57 |->| 56 |->...->| 19 |-+->| 18 |->...->| 1  |->| 0  |--'
        |  '----'  '----'       '----'    '----'       '----'  '----'
        V
    DOUT
                                                                                                            bit width 64            58
                                                                                                            value[pos]
    data_out[0] = data_in[0] ^ state[19] ^ state[0]                                             mask        00.......1[0]    00000....1[19]....1[0]
    data_out[1] = data_in[1] ^ state[20] ^ state[1]                                                         00......1[1]0    00000....1[20]....1[1]0
    data_out[2] = data_in[2] ^ state[21] ^ state[2]                                                         00......1[2]00   00000....1[21]....1[2]00
                                                .................
    data_out[38]= data_in[38] ^ state[57] ^ state[38]                                                       00..1[38]..000   1[57]0000...1[38]...000

    data_out[39]= data_in[39] ^ data_out[0] ^ state[39]  =   data_in[39] ^ data_in[0] ^ state[19] ^ state[0] ^ state[39]     00..1[39]..001[0]   00000...1[39]..1[19]..001[0]

***************************************************************************/

module eth10G_64b66b_scrambler (
    input  wire [63:0] data_in,
    input  wire [57:0] state_in,
    output reg  [63:0] data_out,
    output reg  [57:0] state_out
);

    localparam POLY = 58'h8000000001;//x58 + x39 + 1

    // integer i;
    // always @(*) begin
    //     state_out = state_in;
    //     for(i = 0; i < 64; i = i + 1) begin
    //         state_out = {state_out[56:0], data_in[i] ^ state_out[57] ^ state_out[38]};
    //         data_out[i] = state_out[0];
    //     end
    // end

    integer i;
    always @(*) begin
        state_out = state_in;
        for(i = 0; i < 64; i = i + 1) begin
            state_out = {data_in[i] ^ state_out[0] ^ state_out[19],state_out[57:1]};
            data_out[i] = state_out[57];
        end
    end

endmodule

下面这个是解扰：

/*****************************************************************************
Fibonacci feed-forward style (example for 64b66b descrambler, 0x8000000001)

   DIN (LSB first)
    |
    |  .----.  .----.       .----.    .----.       .----.  .----.
    +->|  0 |->|  1 |->...->| 38 |-+->| 39 |->...->| 56 |->| 57 |--.
    |  '----'  '----'       '----' |  '----'       '----'  '----'  |
    |                              V                               |
   (+)<---------------------------(+)------------------------------'
    |
    V
   DOUT

    DIN (LSB first)
    |
    |  .----.  .----.       .----.    .----.       .----.  .----.
    +->| 57 |->| 56 |->...->| 19 |-+->| 18 |->...->| 1  |->| 0  |--.
    |  '----'  '----'       '----' |  '----'       '----'  '----'  |
    |                              V                               |
   (+)<---------------------------(+)------------------------------'
    |
    V
   DOUT                                                                                                     bit width 64            58
                                                                                                            value[pos]
    data_out[0] = data_in[0] ^ state[19] ^ state[0]                                             mask        00.......1[0]    00000....1[19]....1[0]
    data_out[1] = data_in[1] ^ state[20] ^ state[1]                                                         00......1[1]0    00000....1[20]....1[1]0
    data_out[2] = data_in[2] ^ state[21] ^ state[2]                                                         00......1[2]00   00000....1[21]....1[2]00
                                                .................
    data_out[38]= data_in[38] ^ state[57] ^ state[38]                                                       00..1[38]..000   1[57]0000...1[38]...000

    data_out[39]= data_in[39] ^ data_in[0] ^ state[39]  =      00..1[39]..001[0]   00000...1[39]..00
    data_out[40]= data_in[40] ^ data_in[1] ^ state[40]  =      00..1[40]..01[1]0   00000...1[39]..00
                                                    ...........
    data_out[57]= data_in[57] ^ data_in[18] ^ state[57]  =      1[57]0..1[18]..000   1[57]0000.....00
    data_out[58]= data_in[58] ^ data_in[19] ^ data_in[0] =      1[58]0..1[19]..001[0]   00000.....00       从这里开始，state不参与了，也就是说state的掩码都是0
                                                    ...........
    data_out[63]= data_in[63] ^ data_in[24] ^ data_in[5] =      1[63]0..1[24]..1[5]00000   00000.....00

    state[0] =  state[1];
    state[1] =  state[2];
    state[2] =  state[3];
           .....
    state[56] = state[57];
    state[57] = data_in[0];

*****************************************************************************/

module eth10G_64b66b_descrambler (
    input  wire [63:0] data_in,
    input  wire [57:0] state_in,
    output reg  [63:0] data_out,
    output reg  [57:0] state_out
);

    localparam POLY = 58'h8000000001;//x58 + x39 + 1

    integer i;
    always @(*) begin
        state_out = state_in;
        for(i = 0; i < 64; i = i + 1) begin
            data_out[i] = data_in[i] ^ state_out[19] ^ state_out[0];
            state_out = {data_in[i], state_out[57:1]};
        end
    end

endmodule

使用for语句，代码看着就很简单。

同理，CRC32的运算也是类似：

module crc32(
    input wire [63:0] data_in,
    input wire [31:0] state_in,
    // output wire [63:0] data_out,
    output wire [31:0] crc_out
);
    //x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1
    localparam POLY = 32'hEDB88320; //reverse 32'h04c11db7
    function [31:0] state_out (input data, input [31:0] state_in);
        integer i;
        begin
            for (i = 31; i >= 0; i = i - 1) begin
                if (i==31)
                    state_out[i] = data ^ state_in[0];
                else if (POLY[i])
                    state_out[i] = state_out[31] ^ state_in[i+1];
                else
                    state_out[i] = state_in[i+1];
            end
        end
    endfunction

    integer i;
    reg [31:0] state_nxt;
    assign crc_out = state_nxt;
    always @(*) begin
        state_nxt = state_in;
        for(i = 0; i < 64; i = i + 1) begin
            state_nxt = state_out (data_in[i], state_nxt);
        end
    end

endmodule

它实现了64位数据的crc32计算，其实就是把1位的运算展开迭代了64次，也可以理解为串转并的过程，代价就是当进数位宽很大时，组合逻辑过长，频率高时序就过不了，lfsr常见的地方是生成随机序列，还有一些校验的地方，比如xilinx一些通信类的IP，example design里会用到PRBS，这个叫pseudo—Random Binary Sequence，叫伪随机2进制序列，这个其实就是基于LFSR做的。

参：

• https://zhuanlan.zhihu.com/p/366067972
• https://blog.csdn.net/lum250/article/details/124375678
• https://profile.iiita.ac.in/bibhas.ghoshal/lecture_slides_coa/LFSR_CRC.pdf