代码随想录第二十一天 | Leecode 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树

Leecode 669. 修剪二叉搜索树

题目描述

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

• 示例 1：

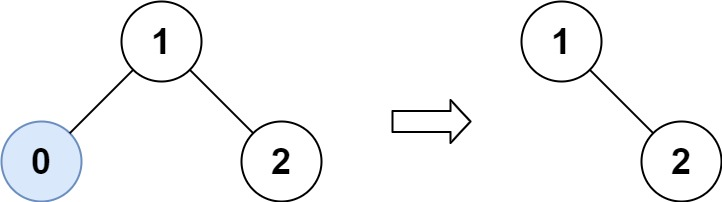
输入：root = [1,0,2], low = 1, high = 2

输出：[1,null,2]

• 示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3

输出：[3,2,null,1]

递归法解题思路与代码

本题要求修剪二叉搜索树中大于和小于目标区间的节点，最基本的是需要知道二叉搜索树的性质，其向下投影（中序遍历）即为有序序列。其次的关键在于要对每个节点的可能情形都进行分类讨论，此时需要注意不能漏掉某一情形，同时要清晰对于每种情况都要如何操作。首先我们先讨论如何来进行分情况讨论。

每个节点的值可能取到的大小0 <= low <= high <= 10^4，同时我们需要保留其中取值在[low, high]闭区间内的值，那么就相当于把数轴划分为三段，分别为：

• [0，low)，在代码中可以具体表示为Node->val < low；
• [low, high]，即Node->val >= low && Node->val <= high；
• (high, 10^4]，即Node->val > high。

根据上面的分类情况，就能考虑到每一个节点的所有情况，接下来我们再说明对于其中每一种情况需要如何处理：

• 当Node->val < low时，当前节点及其左子树都不满足条件，但是右子树是否满足还未知。因此可以考虑使用右子节点来替代当前节点，继续递归处理当前节点
• 当Node->val >= low && Node->val <= high时，当前节点满足条件，此时递归处理左右子树
• 当Node->val > high时，类似第一种情况，右子树和当前节点都不满足，用左子节点来替代当前节点。并再将当前节点传入递归

根据上面算法思想，即可实现如下代码：

class Solution {
public:
    void cutHelper(TreeNode*& curNode, int low, int high){
        if(!curNode) return; // 如果当前节点已经为空，则直接返回
        if(curNode->val < low) { // 如果当前节点已经小于下界，则用其右子节点来替代当前节点
            if(curNode->val < low)curNode = curNode->right; // 用右子节点来替代当前节点
            if(curNode)cutHelper(curNode, low, high); // 继续将当前节点传入递归修剪（因当前节点已经被替换，所以继续传当前节点）
        }
        else if(curNode->val >= low && curNode->val <= high){ // 如果当前节点满足条件，则需要分别对左右子树进行修剪
             cutHelper(curNode->left, low, high); // 递归修剪左子树
             cutHelper(curNode->right, low, high); // 递归修剪右子树
        }
        else if(curNode->val > high){ // 如果当前节点的值大于上界，则将
            if(curNode->val > high) curNode = curNode->left;
            if(curNode)cutHelper(curNode, low, high);
        }
    }

    TreeNode* trimBST(TreeNode* root, int low, int high) {
        cutHelper(root, low, high);
        return root;
    }
};

上面代码的最坏时间复杂度为\(O(n)\)，即每个节点都需要进行一次判断，判断其是否落在区间内。但实际上每次判断后根据二叉搜索树的性质，可以知道当前节点左右子树是否有可能满足，从而省略一部分判断用时从而减少时间复杂度。

Leecode 108. 将有序数组转换为二叉搜索树

题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

• 示例 1：

输入：nums = [-10,-3,0,5,9]

输出：[0,-3,9,-10,null,5]

解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

• 示例 2：

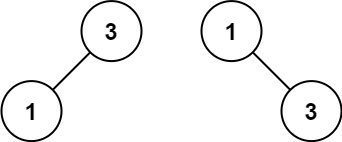
输入：nums = [1,3]

输出：[3,1]

解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

解题思路与代码展示

本题是建立二叉树的题目，此前已经做过几道类似的题目。关键在于划分数组，以用于建立当前节点的值作为分割点，将数组分为两半，并后续分别用于递归构造左右子树。本题特别的点在于是需要建立平衡的二叉搜索树，为了平衡性，我们可以考虑每次使用当前数组的中点作为当前节点的值并对数组进行分割，这样就可以保证左右子树中的节点个数只相差1，从而确保了平衡性。

class Solution {
public:
    void buildHelper(TreeNode*& curRoot, vector<int> curVec){
        if(curVec.empty()) return; // 如果当前向量已经为空，则直接返回
        int cutPoint = curVec.size()/2 ; // 使用有序数组的中点作为分割点
        curRoot = new TreeNode(curVec[cutPoint]); // 使用中点值来建立当前节点

        vector<int> leftVec(curVec.begin(), curVec.begin()+cutPoint); // 建立左子数组
        buildHelper(curRoot->left, leftVec);  // 递归建立左子树

        vector<int> rightVec(curVec.begin()+cutPoint+1,curVec.end()); // 建立右子数组
        buildHelper(curRoot->right, rightVec); // 递归建立右子树

        return;
    }

    TreeNode* sortedArrayToBST(vector<int>& nums) {
        TreeNode* root = nullptr; // 讨论空节点的情况
        buildHelper(root, nums); // 调用递归函数进行建树
        return root;
    }
};

Leecode 538. 把二叉搜索树转换为累加树

题目描述

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。

节点的右子树仅包含键 大于 节点键的节点。

左右子树也必须是二叉搜索树。

• 示例 1：

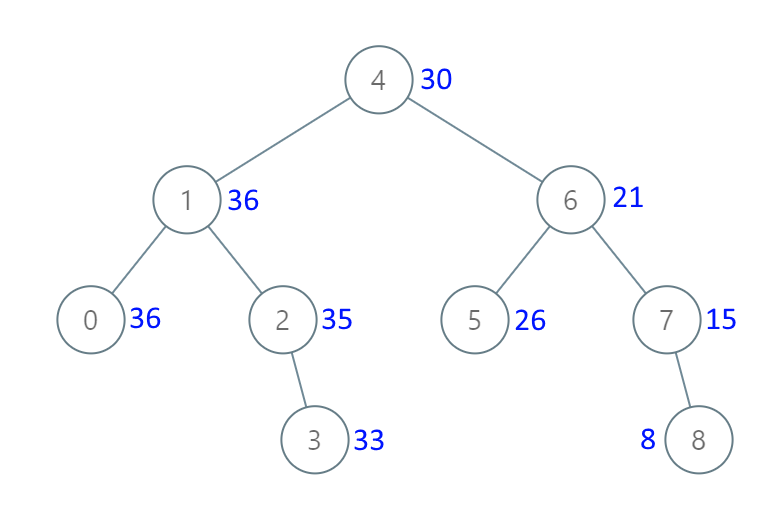
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]

输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

• 示例 2：

输入：root = [0,null,1]

输出：[1,null,1]

• 示例 3：

输入：root = [1,0,2]

输出：[3,3,2]

• 示例 4：

输入：root = [3,2,4,1]

输出：[7,9,4,10]

递归法 解题思路与代码

本题使用递归来进行深度优先算法。因为要将每个节点转换为本身与右边所有节点的和，所以可以知道一开始必须走到最左边的那个节点并记录求和值。只要能够想通深度优先就是中序遍历，那么本题就没有什么难度了。直接在中序遍历递归的基础上，将其更改为记录求和并更新当前节点的操作即可。故有下面代码：

class Solution {
public:
    void convertHelper(TreeNode* curNode, int& sum){ // 使用中序遍历来进行递归
        if(!curNode) return; // 如果当前节点为空则返回
        convertHelper(curNode->right, sum); // 向右递归

        sum += curNode->val;  // 将当前节点值加到sum上
        curNode->val = sum;  // 在令当前节点值等于sum

        convertHelper(curNode->left, sum); // 向左递归
    }

    TreeNode* convertBST(TreeNode* root) {
        int sum = 0;
        convertHelper(root, sum);
        return root;
    }
};

时间复杂度为\(O(n)\)，即每个节点遍历一次。

今日总结

实际上是昨日总结...因为本来该4.15发的打卡到了4.16才发，原因是昨天去看了DragonForce北京演出。

发现二叉树部分的题目暂时算是刷完了，总的来说感觉大部分题目用递归来解决都并不算难，关键在于说要去往前、中、后序遍历的方向去套。以及递归中需要分情况讨论的地方要把所有可能性都考虑到，那么就基本都能做出来。

同时还有一个非常重要的点在于，在层序遍历中使用队列来解决问题的范式模板，注意当需要分层解决问题的时候，需要固定每一次循环开始时的队列长度，用于表示当前层的节点个数。

二叉树最难的地方感觉就在于，使用迭代来求解的时候，对于前序遍历和中序遍历的迭代法需要充分掌握。还有就是当遇到需要自下而上的算法的时候，需要使用回溯的方式。对于回溯算法，如果使用递归来实现，使用值传递可以免去一次pop出栈操作，但是值传递可能会导致每一次递归都复制一个栈，当数据量较大时会占用很大的空间。如果使用引用的方式进行回溯，则每次递归之后要手动使用pop进行回溯。

大致上总结了一下最近学到的东西，以及记录当前力扣进度：

目前力扣已经79题了，100题尽在眼前，继续加油