计数类 dp 做题记录（长期更新）

前言

因为本人太弱，急需锻炼思维，固从现在起开始着手写计数题，并写下题解分析思路的欠缺。另外本文将长时间更新，所以我准备把它置顶，尽量日更！

upd on 24.11.6

现版本改成长期更新。

P3643 [APIO2016] 划艇 2024.8.28

简要题意

现在有 \(n\) 个区间，每个区间范围为 \([l_i,r_i]\)。现在有 \(n\) 个元素需要赋值，每个元素的值要么为零，要么在给定的区间内。对于一个值非零的元素 \(a_i\)，需要满足它的数值严格大于所有标号比它小的元素，即 \(a_i\ge\max_{1\le j<i}\{a_j\}\)。求方案数。

数据范围：\(n\le500,1\le l_i\le r_i\le10^9\)。

题解

首先去想题目性质，然后很高兴地发现根本没有什么性质。然后先考虑朴素 dp，我们令 \(f_{i,j}\) 表示第 \(i\) 个元素值为 \(j\) 的方案数，最后答案为 \(\sum_{i=1}^{i\le n}\sum_{j}f_{i,j}\)。

然后考虑转移，其实转移也很暴力我就直接放式子了：

\[f_{i,j}=\begin{cases}
\sum_{k=0}^{i-1}\sum_{l=1}^{j-1}f_{k,l} & j\in[l_i,r_i]\\
0 & otherwise
\end{cases}
\]

为方便转移，初始 \(f_{0,1}=1\)。

然后不用多说这个肯定爆了。第二维值域是 \(10^9\) 所以能够想到将区间离散化，然后第二维改成区间。这样转移就需要小小的改变一下，因为涉及到了区间选若干点，所以需要加一个系数。那么系数我们怎么求呢？

假设当前区间长度为 \(len\)，元素为第 \(i\) 个。枚举到前 \(j\) 个元素时，现在有 \(i-j\) 个元素将会放在当前区间，我们就把问题抽象成有 \(1\) 到 \(len\) 一共 \(len\) 个数，我们需要从中选出最多 \(m\) 个，选择的方案数就是转化时乘上的系数。考虑对于一次选择，我可以选或不选，若我选就会从中选取一个数就正常做；但如果我不选呢？就把它看成我选了零。于是我们就可以往序列中加入 \(m\) 个零，现在有一共 \(len+m\) 个数，我要从中选出 \(m\) 个，方案为 \({len+m}\choose m\)。然而因为 dp 状态钦定第 \(i\) 个数必选，所以我们实际往序列中加入的零的个数应该会比上述操作少一个（因为保证至少有一个数也就是 \(i\) 不为零）。于是最后的 dp 转移就变成了下面的：

\[f_{i,j}=\begin{cases}
\sum_{k=0}^{i-1}\sum_{l=1}^{j-1}f_{k,l}{Len_j+cnt-1\choose cnt} & j\in[l_i,r_i]\\
0 & otherwise
\end{cases}
\]

但是现在总复杂度还是 \(O(n^4)\) 的，还需要一个小优化，然后考虑哪些状态可以一起考虑。我们可以发现，对于当前的状态 \(f_{i,j}\)，我只要满足一个状态 \(f_{k,l}\) 的第二维小于 \(j\) 也就是 \(l<j\)，就可以将所有的 \(f_{k,l},l<j\) 累加然后整体乘上一个组合数，所以记一个 \(g_{i,j}=\sum_{k=1}^{j-1}f_{i,k}\)，然后就得到了最后的转移式：

\[f_{i,j}=\sum_{k=0}^{i-1}g_{k,j}{Len_j+cnt-1\choose cnt}
\]

时间复杂度 \(O(n^3)\) 不做过多解释。

代码

点击查看代码

int n, l[N], r[N], z[N << 1], tot;
ll f[N], c[N], inv[N], ans;
ll add(ll x, ll y){
    x += y; return x >= p ? x - p : x;
}

signed main(){
    // fileio(fil);
    n = rd();
    for(int i = 1; i <= n; ++i){
        z[i - 1 << 1 | 1] = l[i] = rd(), z[i << 1] = r[i] = rd() + 1;
    }
    sort(z + 1, z + 1 + (n << 1));
    tot = unique(z + 1, z + 1 + (n << 1)) - z - 1;
    for(int i = 1; i <= n; ++i){
        l[i] = lower_bound(z + 1, z + 1 + tot, l[i]) - z;
        r[i] = lower_bound(z + 1, z + 1 + tot, r[i]) - z;
    }
    inv[1] = f[0] = c[0] = 1;
    for(int i = 2; i <= n; ++i)inv[i] = 1ll * (p - p / i) * inv[p % i] % p;
    for(int i = 1; i < tot; ++i){
        int len = z[i + 1] - z[i];
        for(int j = 1; j <= n; ++j)c[j] = c[j - 1] * (len + j - 1) % p * inv[j] % p;
        for(int j = n; j; --j)if(l[j] <= i and i + 1 <= r[j]){
            ll s = 0; int cnt = 1;
            for(int k = j - 1; ~ k; --k){
                s = add(s, c[cnt] * f[k] % p);
                cnt += l[k] <= i and i + 1 <= r[k];
            }
            f[j] = add(f[j], s);
        }
    }
    for(int i = 1; i <= n; ++i)ans += f[i];
    printf("%lld", ans % p);
    return 0;
}

小结

其实做完这道题时感觉完全不够紫题，但是在看题解之前怎么都切不了。其实暴力 dp 我肯定会，离散化我想到了，后面的组合数也很基础，最后的前缀和相对于其他优化也简单得多。但是，为什么我就是做不出来呢？因为我不熟悉知识间的组合与衔接，不肯从暴力入手，老是想怎么直接出正解，而真正的正解需要前面大量的铺垫。它或许是 OIer 做题时的妙手偶得，但更是大量的经验与积累！

而对于我来说，我拿到一道题应该去做什么？我首先要去分析题目的性质，然后根据性质看看能不能得出进一步结论。有了以上的东西，我就可以去根据已有的东西思考如何得出答案，这一期间可以先将时间复杂度暂放。最后再来慢慢优化求解的过程，方法。还有不要忘了验证正确性！

AGC30 - D - Inversion Sum 2024.8.29

简要题意

有一个长度为 \(n\) 的序列，现在有 \(q\) 次操作，每次操作都可以交换两个数的位置，对于每次操作可以选择执行或不执行。对于所有的情况求出一共的逆序对数量。

题解

首先要知道一个技巧：在多种情况下计数可以转换成求概率再乘上情况数。

然后就可以将题意转换成求 \(a_i>a_j,i<j\) 的概率和，于是就可以设计一个 dp \(f_{i,j}\) 表示 \(a_i>a_j,i<j\) 的概率。当一次操作交换 \(x,y\) 时，对于所有的 \(f_{x,i},f_{y,i},f_{i,x},f_{i,y}\) 都会改变。就拿 \(f_{x,i}\) 举例，一次操作后它有 \(\frac{1}{2}\) 的概率继承之前的状态，还有 \(\frac{1}{2}\) 的概率变成 \(f_{y,i}\) 的状态，所以转移就是两个状态相加除以二。对于每次操作都需要改变 \(O(n)\) 的状态，时间复杂度 \(O(nq)\)。

代码

点击查看代码

int n, q, a[N];
ll f[N][N];

ll qmi(ll x, int y){
    ll res = 1;
    for(; y; y >>= 1, x = x * x % p)if(y & 1)res = res * x % p;
    return res;
}
const ll i2 = p + 1 >> 1;

ll add(ll x, ll y){
    x += y; return x >= p ? x - p : x;
}

signed main(){
    // fileio(fil);
    n = rd(), q = rd();
    for(int i = 1; i <= n; ++i)a[i] = rd();
    for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)f[i][j] = a[i] > a[j];
    for(int i = 1; i <= q; ++i){
        int x = rd(), y = rd();
        for(int j = 1; j <= n; ++j)if(j ^ x and j ^ y)f[x][j] = f[y][j] = add(f[x][j], f[y][j]) * i2 % p, f[j][x] = f[j][y] = add(f[j][x], f[j][y]) * i2 % p;
        f[x][y] = f[y][x] = add(f[x][y], f[y][x]) * i2 % p;
    }
    ll s = qmi(2, q), res = 0;
    for(int i = 1; i < n; ++i)for(int j = i + 1; j <= n; ++j)res = add(res, f[i][j]);
    printf("%lld", res * s % p);
    return 0;
}

draw 2024.8.30

简要题意

有一个 \(4\times N\) 的木板需要粉刷，第 \(i\) 行 \(j\) 列的颜色记为 \(A(i,j)\)。 有 256 种颜色，记为 \(0\dots255\)，为了使得粉刷比较好看，粉刷需要满足如下。

要求:

1. \(A(x,y)>=A(x,y-1)\)；
2. 有一些指定的 \((x1,y1)\) 和 \((x2,y2)\) 满足 \(A(x1,y1)=A(x2,y2)\)；

请问有多少种满足要求的粉刷方式？

数据范围

\(1\le n\le15,0\le M\le100\)

题解

先考虑题目性质：

1. 根据要求的第一条，我们可以知道对于一个合法的木板，每一行没有影响，而且每一行的数从小到大单调不减。
2. 题目中的数据范围超级小。

首先如果你单纯想用三维甚至二维 dp 就解决问题可能比较麻烦，既然数据范围很小，我们可以考虑高维 dp 的做法。其实我们可以很自然的想到一个爆炸的 dp，我们考虑 \(f_{i1, c1, i2, c2, i3, c3, i4, c4}\) 表示每一行填到某一位以及当前位置的颜色它的方案数。然后可以把这个东西抽象成有四个完全背包，这个状态相当于把四个背包放在一起考虑。对于每个背包，有无数个标号为 \(0\dots255\) 的物品，代价为 1，价值为方案数。然后类似背包直接转移。

然后 dp 爆炸了。考虑优化。其实你会发现上面的 dp 我们没有任何的限制，导致它很混乱，会有很多的状态，导致我们复杂度爆炸。所以我们需要合并一些能够合并的状态。对于上面的状态我们能够确定一点就是每一行的位置是一定要单独维护的，这一点毋庸置疑。但是每一个位置的颜色可以改变，如果没有限制直接记录下来会产生很多状态，所以我们可以每次把颜色统一起来。现在我们换一种 dp 状态，考虑 \(f_{col,i1,i2,i3,i4}\) 表示当前要填的颜色（数）是 \(col\)，我们每一行填到某个位置时的方案数，然后转移就和上面的一样，可以类比一下。

至于要求某的点颜色相等，就是在转移的时候判断一下当前的状态是否合法，也就是对于对应行的填的位置必须都在有限制的位置的同一侧，这个可以预处理一下。最后时间复杂度就是 \(O(256n^4)\)。

代码

点击查看代码

const int N = 20, p = 1e5, M = 105;
int n, m, o[N][N][N][N], xx[M], yy[M], _x[M], _y[M], ii[5];
int f[N][N][N][N];

signed main(){
    freopen("draw.in", "r", stdin);
    freopen("draw.out", "w", stdout);
    n = rd(), m = rd();
    for(int i = 1; i <= m; ++i)xx[i] = rd(), yy[i] = rd(), _x[i] = rd(), _y[i] = rd();
    for(int i = 1; i <= m; ++i)for(ii[1] = 0; ii[1] <= n; ++ii[1])for(ii[2] = 0; ii[2] <= n; ++ii[2])
        for(ii[3] = 0; ii[3] <= n; ++ii[3])for(ii[4] = 0; ii[4] <= n; ++ii[4])o[ii[1]][ii[2]][ii[3]][ii[4]] |= ii[xx[i]] >= yy[i] ^ ii[_x[i]] >= _y[i];
    f[0][0][0][0] = 1;
    for(int c = 0; c < 256; ++c){
        for(int i = 1; i < 5; ++i)for(ii[1] = 0; ii[1] <= n; ++ii[1])for(ii[2] = 0; ii[2] <= n; ++ii[2])
            for(ii[3] = 0; ii[3] <= n; ++ii[3])for(ii[4] = 0; ii[4] <= n; ++ii[4]){
                int nkp = f[ii[1]][ii[2]][ii[3]][ii[4]];
                if(++ii[i] <= n)(f[ii[1]][ii[2]][ii[3]][ii[4]] += nkp) %= p;
                --ii[i];
            }
        for(ii[1] = 0; ii[1] <= n; ++ii[1])for(ii[2] = 0; ii[2] <= n; ++ii[2])for(ii[3] = 0; ii[3] <= n; ++ii[3])
            for(ii[4] = 0; ii[4] <= n; ++ii[4])if(o[ii[1]][ii[2]][ii[3]][ii[4]])f[ii[1]][ii[2]][ii[3]][ii[4]] = 0;
    }
    printf("%05d", f[n][n][n][n]);
    return 0;
}

小结&反思

我在考试的时候被硬控了很久，然后就是感觉思维没打开，不敢去想最开始的八维 dp，只限制于二维到三维，结果转移一直写不出来，但好像 max 有一种神秘做法，好像跟我的想法差不多，思路几乎一模一样，我只差最后一个地方的转移没有想清楚，但是考试时我没有笃定我的信念想下去，非常可惜！然后最近 hfu 也跟我聊过，他也提到了我的这个弱点，我的确应当及时反思，但是越在关键时候越要相信自己，我就没有这种冲劲，太过拘泥。我以后要注意不要给自己一些紧迫感、压抑感，要学会放松、学会顺着自己的想法，不要太在意他们的指点！

Road of the King 2024.9.6

简要题意

有一个 \(n\) 个点的图，目前一条边都没有。

有一个人在 \(1\) 号点要进行 \(m\) 次移动，终点不必是 \(1\) 号点，假设第 \(i\) 次从 \(u\) 移动到 \(v\)，那么在 \(u\) 与 \(v\) 之间连一条有向边。

问有多少种序列能满足：最终 \(n\) 个点组成的图是一个强连通图。答案对 \(10^9+7\) 取模。

数据范围

\(1\le n,m\le 300\)

题解

对于这种连通图计数类问题，有一个常见的套路，就是你去考虑 \(1\) 号点的连通情况。就比如这一道题我们需要考虑现在一共走到过哪一些点，以及一号点所在的强连通分量大小。根据这个思路可以很容易的写出状态 \(f_{i,j,k}\) 表示走了 \(i\) 步，一共走到过 \(j\) 个点，其中一号点所在的强连通分量大小为 \(k\)。

我们可以发现一个性质，就是如果现在去走一个在一号点所在的强连通分量中的点，那么目前所有点都会变成一个强连通分量（显然）。所以状态的转移也就差不多出来了。

但是如果正常转移你会发现很难写，对于一个状态 \(f_{i,j,k}\) 有非常多的转移方法，但是从 \(f_{i,j,k}\) 转移到其他地方就要简单很多，外面可以分三种情况讨论：

1. 下一步走之前没走过的点：\(f_{i+1,j+1,k}=f_{i,j,k}\times(n-j)\)；
2. 下一步走之前走过但是不在一号点所在强连通分量中的点：\(f_{i+1,j,k}=f_{i,j,k}\times(j-k)\)；
3. 下一步走一号点所在强连通分量中的点：\(f_{i+1,j,j}=f_{i,j,k}\times k\)。

最后答案为 \(f_{m,n,n}\)，此题得解！

代码

点击查看代码

int n, m;
ll f[N][N][N];

int add(ll x, int y){
    return x - p + y >= 0 ? x - p + y : x + y;
}

signed main(){
    // fileio(fil);
    n = rd(), m = rd();
    f[0][1][1] = 1;
    for(int i = 0; i < m; ++i)for(int j = 1; j <= n; ++j)for(int k = 1; k <= j; ++k){
        f[i + 1][j + 1][k] = add(f[i + 1][j + 1][k], f[i][j][k] * (n - j) % p);
        f[i + 1][j][k] = add(f[i + 1][j][k], f[i][j][k] * (j - k) % p);
        f[i + 1][j][j] = add(f[i + 1][j][j], f[i][j][k] * k % p);
    }
    cout << f[m][n][n];
    return 0;
}

P9823 [ICPC2020 Shanghai R] The Journey of Geor Autumn 2024.11.20

简要题意

给定 \(1\le k\le n\)，我们规定满足下面性质的排列称为“好排列”：

\(\forall k<i\le n,a_i>\min_{i-k\le j\le i-1}\{a_j\}\)

求好排列的个数对 \(998244353\) 取模。

数据范围：\(1\le n\le 10^7\)。

题解

看到这题首先有一个一眼的 \(O(n^2)\) 暴力，我们设 \(f_{i,j}\) 表示填到第 \(i\) 个位置，已经填的最大的数为 \(j\) 的方案数。然后考虑这一位怎么填。如果不填 \(j\)，就是 \(f_{i,j}\leftarrow f_{i-1,j}\times(j-i+1)\)；如果填 \(j\)，就是 \(f_{i,j}=\sum_{l=j-k}f_{i-1,l}\)。然后考虑第二个转移是一段区间，可以记录一个前缀和优化成 \(O(n^2)\)。

但是这个题数据范围卡的很死，显然是让你寻找线性做法。然后你会发现其实不管你怎么变化，只要第一维记录下标它就一定还需要记录别的东西。

引用大佬 \(\text{max0810}\) 的话来说就是：

枚举下标没前途

所以果断转换第一维的状态，像这种计数题中还可以记录填的数是什么，因为题目中限制条件是大于某个数，所以我们维护前缀最大值。我们可以理解成把 \(1\) 到 \(i\) 之间的数撒在这个排列中合法的方案数。这样就可以做了！

我们设 \(f_i\) 表示填了前 \(i\) 个数的方案数。考虑假设我们已经填了前 \(x\) 个数，下一个填什么？显然可以是 \(x+1\) 到 \(x+k\)。假设我们在里面选择了一个数 \(y\)，那么对于 \(x+1\) 到 \(y-1\) 这些数的填法就没有了要求，对于这些数填入剩下位置的方案数就是 \(A_{n-x-1}^{y-x-1}\)。

然后我们的转移也就呼之欲出了：

\[\forall j-k\le i<j,f_j\leftarrow f_i\times A_{n-i-1}^{j-i-1}
\]

这样虽然状态是 \(O(n)\) 的，但是转移还是带了一个 \(k\)。于是考虑换一种写法，我们从前面的转移到后面，于是有：

\[f_i=\sum_{i-k\le j<i}f_j\times A_{n-j-1}^{i-j-1}
\]

然后把后面的系数拆开：

\[f_i=\sum_{i-k\le j<i}f_j\times\frac{(n-j-1)!}{(n-i)!}
\]

于是我们就记录 \(f_j\times(n-j-1)!\) 的前缀和即可。

代码

点击查看代码

const int N = 1e7 + 5, p = 998244353;

int n, k;
ll f[N], g[N], fac[N], inv[N];

ll qmi(ll x, int y){
	ll res = 1;
	for(; y; y >>= 1, x = x * x % p)if(y & 1)res = res * x % p;
	return res;
}

int main(){
	freopen("b.in", "r", stdin);
	freopen("b.out", "w", stdout);
	n = rd(), k = rd(); fac[0] = inv[0] = 1;
	for(int i = 1; i <= n; ++i)fac[i] = fac[i - 1] * i % p;
	inv[n] = qmi(fac[n], p - 2);
	for(int i = n - 1; i; --i)inv[i] = inv[i + 1] * (i + 1) % p;
	if(k == 1)return puts("1") & 0;
	for(int i = 1; i <= k; ++i)f[i] = fac[n - 1] * inv[n - i] % p;
	for(int i = 1; i <= n; ++i){
		if(i <= k)f[i] = (f[i] + g[i - 1] * inv[n - i]) % p;
		else f[i] = (f[i] + (g[i - 1] + p - g[i - k - 1]) * inv[n - i]) % p;
		g[i] = (g[i - 1] + f[i] * fac[n - i - 1]) % p;
	}
	wt(f[n]);
	return 0;
}

[ARC178D]Delete Range Mex 2024.11.20

简要题意

对于一个排列 \(A\)，每次可以选择一个区间 \([l,r]\) 删去当前排列中的 \(\operatorname{mex}(A_l,A_{l+1}\dots A_r)\) 这个数，可以操作任意次。现在给定一个序列 \(B\)，求长度为 \(n\) 的排列 \(A\) 能够通过若干次操作变成 \(B\) 的 \(A\) 的数量对 \(998244353\) 取模。

数据范围：\(1\le m\le n\le500,0\le B_i<n\)。

题解

对于这道题目我们先去寻找它有什么性质。考虑我们如何删掉一个数 \(x\)？我们需要选择一段区间，满足 \(x\) 不在里面但是小于 \(x\) 的数全在。那么这有什么特殊的呢？我们这样考虑。

加入我们现在要把 \(0\) 到 \(n-1\) 从小到大插入序列，如果我们后面要删除 \(x\)，我们在插入 \(x\) 时就需要把它放在当前序列的最左边或者最右边某个位置（如下图），也就是说当前 \(x\) 可以插入的位置范围是 \([1,lpos)\cup(rpos,n]\)。

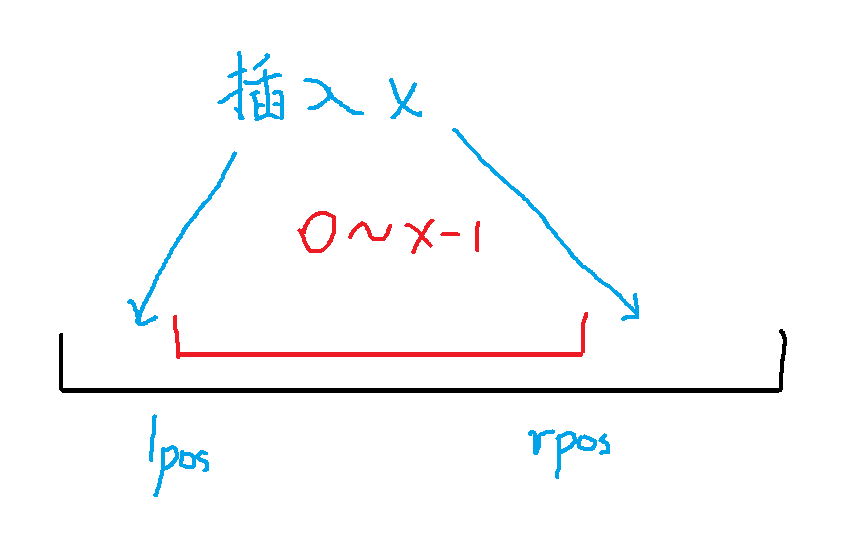
回到此题。现在给出了最后剩下的 \(m\) 个数，而我们需要把删去的数填入这 \(m+1\) 个空中。于是就有 \(f_{l,r,x}\) 表示插入到了 \(x\)，且区间 \([l,r]\) 内不能再填其他数的方案数。

枚举 \(x\)，对于 \(x\)，若 \(x\) 没有被删除，说明它的位置已经确定，我们可以先将其记录下来。转移时就只能转移到旁边的区间：\(f_{\min\{pos_x,l\},\max\{pos_x+1,r\},x}\leftarrow f_{l,r,x-1}\)。因为 \(pos_x\) 不能动。

若 \(x\) 要被删掉，就大概枚举一下 \(x\) 的位置，是一个标准的区间 \(DP\)。当计算到区间 \([l,r]\) 时，\(f_{l,r,x}\) 的转移需要从子区间来，转移式子就是：

\[f_{l,r,x}=\sum_{l\le pos\le r}f_{l,pos,x-1}+\sum_{l\le pos\le r}f_{pos,r,x-1}
\]

解释一下转移。对于一个区间 \([l,r]\) 不能填数，说明最后填 \(x\) 时肯定填在了一个端点。如果填在 \(r\)，子区间就只能在 \([l,pos]\) 中选择，如果填在 \(l\) 同理。然后可以前缀和优化一下，最后时间复杂度 \(O(nm^2)\)。

代码

点击查看代码

const int N = 505, p = 998244353;

int n, m, a[N], pos[N], f[N][N][N];

int add(int x, int y){return x - p + y >= 0 ? x - p + y : x + y;}

int main(){
 	freopen("c.in", "r", stdin);
 	freopen("c.out", "w", stdout);
	n = rd(), m = rd();
	for(int i = 1; i <= m; ++i)a[i] = rd(), pos[a[i]] = i;
	if(pos[0])f[pos[0]][pos[0] + 1][0] = 1;
	else for(int i = 1; i <= m + 1; ++i)f[i][i][0] = 1;
	for(int x = 1; x < n; ++x)if(pos[x])
		for(int i = 1; i <= m + 1; ++i)for(int j = i; j <= m + 1; ++j)
			f[min(pos[x], i)][max(pos[x] + 1, j)][x] = add(f[min(pos[x], i)][max(pos[x] + 1, j)][x], f[i][j][x - 1]);
	else{
		for(int i = 1, tmp = 0; i <= m + 1; ++i, tmp = 0)for(int j = i; j <= m + 1; ++j)
			tmp = add(tmp, f[i][j][x - 1]), f[i][j][x] = add(f[i][j][x], tmp);
		for(int j = 1, tmp = 0; j <= m + 1; ++j, tmp = 0)for(int i = j; i; --i)
			tmp = add(tmp, f[i][j][x - 1]), f[i][j][x] = add(f[i][j][x], tmp);
	}
	wt(f[1][m + 1][n - 1]);
	return 0;
}

ARC132E 2024.12.12

简要题意

有 \(n\) 个方块，每个方块有一个初始状态可能为左右或者空。每次操作随机选择一个空进行操作。每次操作可以向左或者向右走一直到下一个空或者走出边界，走到的每个格子会变成左或者右，这取决于移动方向。

求无法操作时方格为左的期望数。

数据范围：\(n\le 10^5\)。

题解

首先看到这个操作我们可以把每一段方格看成一个整体，以空为分界线，然后最自然的思路就是对于每一个整体考虑对答案的贡献。

然后大概说一下我的想法。就是对于第 \(i\) 个连续段考虑它被更新过和没被更新过两种状态下的贡献。

• 对于没被更新的情况，需要满足对于它左边的空都向左走，右边的空都向右走，贡献就是原始区间中左方格的个数。
• 对于被更新的情况，如果最后被左边向右的覆盖则无贡献，否则就贡献区间长度。

然后经过一番推导你会发现，第二种情况求解的复杂度似乎是 \(O(n)\) 的，然后就炸了。所以我们需要优化一下思路。

我们可以从最终状态入手。

考虑最终的方格状态一定是左边一段左方格，右边一段右方格，然后中间的一段是原始状态。原因显然。

所以我们只用讨论最后哪一段没有被覆盖过，直接枚举是 \(O(n)\) 的。然后对于每一段，它左边的格子都有贡献，它本身的贡献是它原始贡献，它的右边没有贡献。于是我们只用算出它的系数就能求解问题了。

于是我们可以设计一个状态 \(f_n\) 表示让 \(n\) 个连续段都向左且不影响右边放个的状态的概率，考虑从 \(f_{n-1}\) 转移。因为只有最后一个空选择向右走才会不合法，于是就把第 \(n-1\) 的选择方法解放了，所以转移就是 \(f_n=f_{n-1}\times(1-\frac{1}{2n-2})\)。

然后对于枚举段的右边和左边其实是等价的，所以这段的答案就是 \(f_{left}\times f_{right}\times(\operatorname{cnt}_{left}+\operatorname{original}_i)\)。

其中 \(\operatorname{cnt}\) 是前缀个数，\(\operatorname{original}\) 是当前段原始左方格数。

代码

点击查看代码

signed main(){
	for(int i = 1; i <= n; ++i)
		if(a[i] == '<')++cnt;
		else if(a[i] == '.')s[++tot] = i, c[tot] = cnt;
	c[++tot] = cnt; f[1] = 1;
	for(int i = 2; i <= tot; ++i)f[i] = 1ll * f[i - 1] * (p + 1 - qmi(2 * i - 2, p - 2)) % p;
	for(int i = 1; i <= tot; ++i)ans = (0ll + ans + 1ll * f[i] * f[tot - i + 1] % p * (c[i] - c[i - 1] + s[i - 1])) % p;
}

ARC101E 2024.12.25

简要题意

有一棵树，树上有偶数个节点。你需要给这些点两两配对，一组已经配对的点会将两点之间的树边进行一次覆盖。一组合法方案需要满足树上所有边都被覆盖至少一次，求合法方案数。

数据范围：\(n\le5000\)。

思路

首先我们去观察题目性质，发现没有什么特殊的地方。我最开始只想到一个非常暴力的 \(dp\)，设 \(f_{u,i}\) 表示以 \(u\) 为根的子树内有 \(i\) 个点已经匹配好的方案数。但是当我去考虑转移时，我发现他有很多种情况：

1. \(u\) 一个儿子的子树内互相匹配，但是需要有一个点与外面的点匹配（不然这个子树与 \(u\) 之间的边就无法被覆盖）；
2. 一个子树内的点向 \(u\) 的其他子树匹配；
3. 一个子树的点向 \(u\) 子树以外的点匹配。

或许还有一些没有罗列出来，但反正就是不可做。于是我们正难则反，考虑先求出不合法的情况，然后容斥做。

题解

如何求不合法的情况呢？我们可以通过钦定一些边不覆盖来容斥。比如当我计算到以 \(u\) 为根的子树时，我就去枚举 \(u\) 所在的连通块的大小，对于一个 \(u\) 的儿子 \(v\)，分讨一下连通块是否包括 \(v\)。

具体的，我们设 \(f_{u,i}\) 表示以 \(u\) 为根的子树，\(u\) 所在连通块大小为 \(i\) 的方案数。对于 \(v\) 在连通块的时候，有转移：

\[f_{u,i-j}\times f_{v,j}\rightarrow f_{u,i},v\in{\operatorname{son}_u,j<i}
\]

若 \(v\) 与 \(u\) 之间的边不覆盖，则有：

\[f_{u,i}\times f_{v,j}\rightarrow f_{u,i+j}
\]

你乍一看这不就是树上背包吗？时间复杂度 \(O(n^2)\)，可以通过此题！

现在我们已经基本找出状态转移的方程，但现在我们还需要思考一个问题：

一个点数为 \(k\) 的连通块，将里面的点不重不漏两两匹配的方案数

首先对于 \(k\) 为奇数的时候是无贡献的；所以只用考虑 \(k\) 为偶数的情况。考虑递推求解答案，设 \(s_k\) 表示点数为 \(k\) 的贡献。对于一个点，我有 \(k - 1\) 种选择方案，而剩下的 \(k-2\) 个点的方案是 \(s_{k-2}\)，固可得递推式：\(s_{k}=(k-1)\times s_{k-2}\)。

但考虑到我们只是没有考虑这些方案中会有的不合法情况，所以需要稍微容斥一下，在转移的时候还需要给一个 \((-1)^k\)。

然后看到之前的 \(dp\)，我们发现对于第一种情况合并两个连通块似乎不好计算方案，于是我们改写状态，设 \(f_{u,i}\) 表示以 \(u\) 为根的子树，\(u\) 所在连通块大小为 \(i\) 时不考虑 \(u\) 所在连通块中匹配情况的方案数，这样在合并两个连通块时我们就直接把系数乘上就行，所以最后第一种情况的转移式为：

\[f_{u,i}\leftarrow f_{u,i-j}\times f_{v,j}\times(-s_i)
\]

最后答案就是 \(\sum\limits_{i}f_{1, i}\times s_i\)。

代码

点击查看代码

void dfs(int u, int fa){
    sz[u] = f[u][1] = 1;
    for(int i = hd[u]; i; i = e[i].nxt){
        int v = e[i].to; if(v == fa)continue;
        dfs(v, u); copy(f[u], f[u] + 1 + sz[u], g);
        fill(f[u], f[u] + 1 + sz[u], 0);
        for(int j = 1; j <= sz[u]; ++j)for(int k = 1; k <= sz[v]; ++k)
            f[u][j] = del(f[u][j], mul(mul(f[v][k], s[k]), g[j])),
            f[u][j + k] = add(f[u][j + k], mul(g[j], f[v][k]));
        sz[u] += sz[v];
    }
}

P3343地震后的幻想乡 2025.2.12

简要题意

给定一张 \(n\) 个点 \(m\) 条边的图，边的边权是 \([0, 1]\) 之间均匀分布的随机实数，且相互独立。求最小生成树的最大边权的期望值。

思路

首先有一个比较神秘的跟概率有关的东西，虽然题面中已经给出提示，但这里还是进行简单说明：

引理：将长度为 \(n\) 的区间随机划成 \(m\) 段，每段长度期望是 \(n\over m\)。

笔者询问 deepseek，deepseek 给出了三种证明方法，在此仅给出笔者知道的一种。

我们设第 \(i\) 段长度为 \(L_i\)，就有：\(n=\sum\limits_{i=1}^mL_i\)。

根据期望的线性性和对称性我们可以得到：\(n=E(\sum\limits_{i=1}^mL_i)=\sum\limits_{i=1}^mE(L_i)\) 和 \(L_1=L_2=\dots=L_m\)。

所以 \(E(L_i)={n\over m}\)。

所以第 \(k\) 大的边贡献就是 \(k\over m+1\)。我们首先能够有一个 naive 的想法，枚举每个边的大小关系，然后暴力跑 kruskal。这个想法可以启发我们去思考如何统计所有第 \(k\) 大的边的贡献。

首先看每种情况做贡献的概率，确定了选择哪些边要选和哪个边做贡献后就好做了，有 \(P={(k-1)!(m-k)!\over m!}\)。因为期望等于总方案数除以概率，所以现在我们只需要去找方案数，这个就 dp 去求。

因为恰好选第 \(k\) 大的边使图连通不好描述，所以容斥，变成选第 \(k\) 大的边前图不连通的方案数减去选第 \(k\) 大的边后图不连通的方案数。于是就有一个 dp，设 \(f_{S,i}\) 表示 \(S\) 构成的点集中选 \(i\) 条边图不连通的方案，现在考虑枚举子集进行转移。转移就从若干已经连通的子图中选出剩下的一些边，但是不能使整个图连通，所以从严格意义上说是枚举真子集。所以引入 \(g_{S,i}\) 表示 \(S\) 构成的点集中选 \(i\) 条边图连通的方案，就有下面两个转移式：

\[g_{S,i}={d_S\choose i}-f_{S,i}
\]

\[f_{S,i}=\sum_{T\subsetneq S}\sum_{j\le d_T}g_{T,j}{d_{S/T}\choose i-j}
\]

其中 \(d_S\) 为 \(S\) 的导出子图。

最后的答案就是：

\[{1\over m+1}\sum_{i\le m}i({f_{U,i-1}\over{d_U\choose i - 1}}-{f_{U,i}\over{d_U\choose i }})
\]

化简得：

\[{1\over m+1}\sum_{i\le m}{f_{U,i}\over{d_U\choose i }}
\]

代码

点击查看代码

signed main(){
    n = rd(), m = rd();
    for(int i = 1, u, v; i <= m; ++i)u = rd(), v = rd(), ++mp[(1 << u - 1) | (1 << v - 1)];
    for(int S = 1; S < (1 << n); ++S)for(int T = S; T; T = T - 1 & S)d[S] += mp[T];
    c[0][0] = c[1][0] = 1;
    for(int i = 1; i <= m; c[++i][0] = 1)for(int j = 1; j <= i; ++j)c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
    for(int S = 1; S < (1 << n); ++S)for(int i = 0; i <= d[S]; ++i){
        for(int T = S & S - 1; T; T = T - 1 & S)if(T & (S & - S))
            for(int j = 0; j <= min(i, d[T]); ++j)f[S][i] += g[T][j] * c[d[S ^ T]][i - j];
        g[S][i] = 1.0 * c[d[S]][i] - f[S][i];
    }
    for(int i = 0; i <= m; ++i)ans += f[(1 << n) - 1][i] / c[m][i];
    ans /= 1.0 + m;
    printf("%.6f", ans);
    return 0;
}