统计学习方法学习（四）--KNN及kd树的java实现

K近邻法

1基本概念

K近邻法，是一种基本分类和回归规则。根据已有的训练数据集（含有标签），对于新的实例，根据其最近的k个近邻的类别，通过多数表决的方式进行预测。

2模型相关

2.1 距离的度量方式

定义距离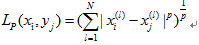

（1）欧式距离：p=2。

（2）曼哈顿距离：p=1。

（3）各坐标的最大值：p=∞。

2.2 K值的选择

通常使用交叉验证法来选取最优的k值。

k值大小的影响：

k越小，只有距该点较近的实例才会起作用，学习的近似误差会较小。但此时又会对这些近邻的实例很敏感，如果紧邻点存在噪声，预测就会出错，即学习的估计误差大，泛化能力不好。

K越大，距该点较远的实例也会起作用，造成近似误差增大，使预测发生错误。

2.3 k近邻法的实现：kd树

　　Kd树是二叉树。kd树是一种对K维空间中的实例点进行存储以便对其进行快速检索的树形数据结构.

　　Kd树是二叉树， 表示对K维空间的一个划分（ partition).构造Kd树相 当于不断地用垂直于坐标轴的超平面将k维空间切分， 构成一系列的k维超矩形区域.Kd树的每个结点对应于一个k维超矩形区域

　　其中，创建kd树时，垂直于坐标轴的超平面垂直的坐标轴选择是：

　　L=(J mod k)+1。其中，j为当前节点的节点深度，k为k维空间（给定实例点的k个维度）。根节点的节点深度为0.此公式可看为：依次循环实例点的k个维所对应的坐标轴。

　　Kd树的节点（分割点）为L维上所有实例点的中位数。

2.4 Kd树的实现

　　别处代码实现基于其他博客，但是纠正了其中的错误，能够返回前k个近邻。如果要求最近邻，只需要将k=1即可。

　　

 public class BinaryTreeOrder {

     public void preOrder(Node root) {
         if(root!= null){
             System.out.print(root.toString());
             preOrder(root.left);
             preOrder(root.right);
         }
     }
 }

public class kd_main {

    public static void main(String[] args) {
        List<Node> nodeList=new ArrayList<Node>();

        nodeList.add(new Node(new double[]{5,4}));
        nodeList.add(new Node(new double[]{9,6}));

        nodeList.add(new Node(new double[]{8,1}));
        nodeList.add(new Node(new double[]{7,2}));
        nodeList.add(new Node(new double[]{2,3}));
        nodeList.add(new Node(new double[]{4,7}));
        nodeList.add(new Node(new double[]{4,3}));
        nodeList.add(new Node(new double[]{1,3}));

        kd_main kdTree=new kd_main();
        Node root=kdTree.buildKDTree(nodeList,0);
        new BinaryTreeOrder().preOrder(root);
        for (Node node : nodeList) {
            System.out.println(node.toString()+"-->"+node.left.toString()+"-->"+node.right.toString());
        }
        System.out.println(root);
        System.out.println(kdTree.searchKNN(root,new Node(new double[]{2.1,3.1}),2));
        System.out.println(kdTree.searchKNN(root,new Node(new double[]{2,4.5}),1));
        System.out.println(kdTree.searchKNN(root,new Node(new double[]{2,4.5}),3));
        System.out.println(kdTree.searchKNN(root,new Node(new double[]{6,1}),5));

    }

    /**
     * 构建kd树  返回根节点
     * @param nodeList
     * @param index
     * @return
     */
    public Node buildKDTree(List<Node> nodeList,int index)
    {
        if(nodeList==null || nodeList.size()==0)
            return null;
        quickSortForMedian(nodeList,index,0,nodeList.size()-1);//中位数排序
        Node root=nodeList.get(nodeList.size()/2);//中位数 当做根节点
        root.dim=index;
        List<Node> leftNodeList=new ArrayList<Node>();//放入左侧区域的节点  包括包含与中位数等值的节点-_-
        List<Node> rightNodeList=new ArrayList<Node>();

        for(Node node:nodeList)
        {
            if(root!=node)
            {
                if(node.getData(index)<=root.getData(index))
                    leftNodeList.add(node);//左子区域 包含与中位数等值的节点
                else
                    rightNodeList.add(node);
            }
        }

        //计算从哪一维度切分
        int newIndex=index+1;//进入下一个维度
        if(newIndex>=root.data.length)
            newIndex=0;//从0维度开始再算

        root.left=buildKDTree(leftNodeList,newIndex);//添加左右子区域
        root.right=buildKDTree(rightNodeList,newIndex);

        if(root.left!=null)
            root.left.parent=root;//添加父指针
        if(root.right!=null)
            root.right.parent=root;//添加父指针
        return root;
    }

    /**
     * 查询最近邻
     * @param root kd树
     * @param q 查询点
     * @param k
     * @return
     */
    public List<Node> searchKNN(Node root,Node q,int k)
    {
        List<Node> knnList=new ArrayList<Node>();
        searchBrother(knnList,root,q,k);
        return knnList;
    }

    /**
     * searhchBrother
     * @param knnList
     * @param k
     * @param q
     */
    public void searchBrother(List<Node> knnList, Node root, Node q, int k) {
//         Node almostNNode=root;//近似最近点
         Node leafNNode=searchLeaf(root,q);
         double curD=q.computeDistance(leafNNode);//最近近似点与查询点的距离 也就是球体的半径
         leafNNode.distance=curD;
         maintainMaxHeap(knnList,leafNNode,k);
         System.out.println("leaf1"+leafNNode.getData(leafNNode.parent.dim));
         while(leafNNode!=root)
         {
             if (getBrother(leafNNode)!=null) {
                 Node brother=getBrother(leafNNode);
                 System.out.println("brother1"+brother.getData(brother.parent.dim));
                 if(curD>Math.abs(q.getData(leafNNode.parent.dim)-leafNNode.parent.getData(leafNNode.parent.dim))||knnList.size()<k)
                 {
                     //这样可能在另一个子区域中存在更加近似的点
                     searchBrother(knnList,brother, q, k);
                 }
            }
           System.out.println("leaf2"+leafNNode.getData(leafNNode.parent.dim));
           leafNNode=leafNNode.parent;//返回上一级
           double rootD=q.computeDistance(leafNNode);//最近近似点与查询点的距离 也就是球体的半径
           leafNNode.distance=rootD;
           maintainMaxHeap(knnList,leafNNode,k);
          }
     }

    /**
     * 获取兄弟节点
     * @param node
     * @return
     */
    public Node getBrother(Node node)
    {
        if(node==node.parent.left)
            return node.parent.right;
        else
            return node.parent.left;
    }

    /**
     * 查询到叶子节点
     * @param root
     * @param q
     * @return
     */
    public Node searchLeaf(Node root,Node q)
    {
        Node leaf=root,next=null;
        int index=0;
        while(leaf.left!=null || leaf.right!=null)
        {
            if(q.getData(index)<leaf.getData(index))
            {
                next=leaf.left;//进入左侧
            }else if(q.getData(index)>leaf.getData(index))
            {
                next=leaf.right;
            }else{
                //当取到中位数时  判断左右子区域哪个更加近
                if(q.computeDistance(leaf.left)<q.computeDistance(leaf.right))
                    next=leaf.left;
                else
                    next=leaf.right;
            }
            if(next==null)
                break;//下一个节点是空时  结束了
            else{
                leaf=next;
                if(++index>=root.data.length)
                    index=0;
            }
        }

        return leaf;
    }

    /**
     * 维护一个k的最大堆
     * @param listNode
     * @param newNode
     * @param k
     */
    public void maintainMaxHeap(List<Node> listNode,Node newNode,int k)
    {
        if(listNode.size()<k)
        {
            maxHeapFixUp(listNode,newNode);//不足k个堆   直接向上修复
        }else if(newNode.distance<listNode.get(0).distance){
            //比堆顶的要小   还需要向下修复 覆盖堆顶
            maxHeapFixDown(listNode,newNode);
        }
    }

    /**
     * 从上往下修复  将会覆盖第一个节点
     * @param listNode
     * @param newNode
     */
    private void maxHeapFixDown(List<Node> listNode,Node newNode)
    {
        listNode.set(0, newNode);
        int i=0;
        int j=i*2+1;
        while(j<listNode.size())
        {
            if(j+1<listNode.size() && listNode.get(j).distance<listNode.get(j+1).distance)
                j++;//选出子结点中较大的点，第一个条件是要满足右子树不为空

            if(listNode.get(i).distance>=listNode.get(j).distance)
                break;

            Node t=listNode.get(i);
            listNode.set(i, listNode.get(j));
            listNode.set(j, t);

            i=j;
            j=i*2+1;
        }
    }

    private void maxHeapFixUp(List<Node> listNode,Node newNode)
    {
        listNode.add(newNode);
        int j=listNode.size()-1;
        int i=(j+1)/2-1;//i是j的parent节点
        while(i>=0)
        {

            if(listNode.get(i).distance>=listNode.get(j).distance)
                break;

            Node t=listNode.get(i);
            listNode.set(i, listNode.get(j));
            listNode.set(j, t);

            j=i;
            i=(j+1)/2-1;
        }
    }

    /**
     * 使用快排进进行一个中位数的查找  完了之后返回的数组size/2即中位数
     * @param nodeList
     * @param index
     * @param left
     * @param right
     */
    @Test
    private void quickSortForMedian(List<Node> nodeList,int index,int left,int right)
    {
        if(left>=right || nodeList.size()<=0)
            return ;

        Node kn=nodeList.get(left);
        double k=kn.getData(index);//取得向量指定索引的值

        int i=left,j=right;

        //控制每一次遍历的结束条件，i与j相遇
        while(i<j)
        {
            //从右向左找一个小于i处值的值，并填入i的位置
            while(nodeList.get(j).getData(index)>=k && i<j)
                j--;
            nodeList.set(i, nodeList.get(j));
            //从左向右找一个大于i处值的值，并填入j的位置
            while(nodeList.get(i).getData(index)<=k && i<j)
                i++;
            nodeList.set(j, nodeList.get(i));
        }

        nodeList.set(i, kn);

        if(i==nodeList.size()/2)
            return ;//完成中位数的排序了，但并不是完成了所有数的排序，这个终止条件只是保证中位数是正确的。去掉该条件，可以保证在递归的作用下，将所有的树
                    //将所有的数进行排序

        else if(i<nodeList.size()/2)
        {
            quickSortForMedian(nodeList,index,i+1,right);//只需要排序右边就可以了
        }else{
            quickSortForMedian(nodeList,index,left,i-1);//只需要排序左边就可以了
        }

//        for (Node node : nodeList) {
//            System.out.println(node.getData(index));
//        }
    }
}

public class Node implements Comparable<Node>{
    public double[] data;//树上节点的数据  是一个多维的向量
    public double distance;//与当前查询点的距离  初始化的时候是没有的
    public Node left,right,parent;//左右子节点  以及父节点
    public int dim=-1;//维度  建立树的时候判断的维度

    public Node(double[] data)
    {
        this.data=data;
    }

    /**
     * 返回指定索引上的数值
     * @param index
     * @return
     */
    public double getData(int index)
    {
        if(data==null || data.length<=index)
            return Integer.MIN_VALUE;
        return data[index];
    }

    @Override
    public int compareTo(Node o) {
        if(this.distance>o.distance)
            return 1;
        else if(this.distance==o.distance)
            return 0;
        else return -1;
    }

    /**
     * 计算距离 这里返回欧式距离
     * @param that
     * @return
     */
    public double computeDistance(Node that)
    {
        if(this.data==null || that.data==null || this.data.length!=that.data.length)
            return Double.MAX_VALUE;//出问题了  距离最远
        double d=0;
        for(int i=0;i<this.data.length;i++)
        {
            d+=Math.pow(this.data[i]-that.data[i], 2);
        }

        return Math.sqrt(d);
    }

    public String toString()
    {
        if(data==null || data.length==0)
            return null;
        StringBuilder sb=new StringBuilder();
        for(int i=0;i<data.length;i++)
            sb.append(data[i]+" ");
        sb.append(" d:"+this.distance);
        return sb.toString();
    }
}

　　参考文献：

　　　　[1]李航.统计学习方法