算法改进 | java语言中判断素数

参考文章：http://blog.csdn.net/kp_liu/article/details/37569507

http://blog.csdn.net/huang_miao_xin/article/details/51331710

https://www.zybang.com/question/93c4703c84c5ad3c1c34b1e6672b0568.html

素 数

——只能被1和它本身整除的数（除1以外，1既不是素数也不是合数）

• • • • • • • 现给出一个数N（N为正整数），编写方法判断其是否为素数。

直观想法

遍历从2至N-1，看是否存在N的约数。若存在，即不是素数。

基础改进

不必从2遍历至N-1，数N若是合数，则其至少可由两个因数相乘得到，这两个数必定一个大于（或等于）sqrt(n)，一个小于（或等于）sqrt(n)，因此仅需遍历至sqrt(n)即可。

改进方法一 （偶数；缩小判断范围；）

Step 1 （除2以外）判断N是否为偶数，若是，则判断结束——不是素数；

Step 2  若N不是偶数但是合数，它的因数绝不可能是偶数（原因 偶数×偶数=偶数；偶数×奇数=偶数），

因此判断奇数N的因数时，可以省去对偶数的判断。(i+=2)

 static boolean isPrime_1(int N){
          int tmp=(int)Math.sqrt(N);
          //Step 1
          if(N==2)return true;
          if(N%2==0)return false;
          //Step 2
          for(int i=3;i<tmp;i+=2)
              if(N%i==0)return false;

          return true;
      }

改进方法二 （质数分布规律；pruning策略；）

一个关于质数分布的规律：大于等于5的质数一定和6的倍数相邻（即大于等于5的质数x,都可以表示为x=6k+1 或者是 x=6k-1,k为>0的自然数）。

但要注意：在6的倍数相邻两侧并不是一定就是质数。

证明

直观看，大于等于5的自然数都可以用6k-1，6k，6k+1，6k+2，6k+3，6k+4，6k+5的形式表示，显然6k+2 = 2(3k+2)，6k+3 = 3(2k+1)，6k+4 = 2(3k+2)都是合数，再除去6k本身，因此大于等于5的质数都可以表示成6k+1和6k+5（当x大于等于6时，6k+5与6k-1可表示同一个数）的形式。

数学证明

• 质数x大于等于5，则一定不是3的倍数，也不是2的倍数。
• 如果一个自然数不是3的倍数，有两种情况，设 x=3p+1或x=3p+2 (p>1)
• 如果一个自然数不是2的倍数，有一种情况，设 x=2t+1 (t>3)

1）若x=3p+1，且x=2t+1

则x=3p+1=2t+1 >> x-1=3p=2t

>> 3p=2t，可知p为2的倍数，t为3的倍数，

设p=2k，>> t=3k

因此x=2*3k+1=6k+1

2）若x=3p+2，且x=2t+1

则x=3p+2=2t+1

>> 3p+1=2t，因此3p为奇数，即p为奇数，设p=2k-1

则3*(2k-1)+1=2t，>> t=3k-1

因此x=2(3k-1)+1=6k-1

Step 1  单独判断2、3，都是素数；

Step 2  判断N是否在6的倍数的两侧，若不在，则判断结束——不是素数；

Step 3  数N在6的倍数两侧也不一定是质数，还需判断是否能在6的倍数两侧的数中找到数N的因数，若找不到，才可判定为质数。

（为什么只需在“6的倍数两侧的数”中寻找因数？

原因 所有合数可由质数的积组成，所以N只需要与可能是质数（即6的倍数的前后两个数）的数进行取余）

 static boolean isPrime_2(int N){
          int tmp=(int)Math.sqrt(N);
          //Step 1
          if(N==2||N==3)return true;
          //Step 2
          if(N%6!=1&&N%6!=5)return false;
          //Step 3
          for(int i=5;i<=tmp;i+=6)
              if(N%i==0||N%(i+2)==0)return false;
          /*此处
           * i表示形式为6k+5的数，
           * i+2表示形式为6k+1的数
           */

          return true;
      }

方法比较 && 代码测试

测试代码

数据情况

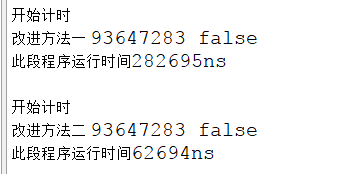
• • • • • • • “改进方法二” 完胜

---

E N D